DesTec - Revisão e Conceitos (PRONATEC)

Medidas de comprimento
Transformando 1 metro (m) em milímetros (mm):
1º passo: transformar metro em decímetro
2º passo: transformar decímetro em centímetro
3º passo: transformar centímetro em milímetro
Para ser mais prático, podemos multiplicar o metro por 10x10x10 (1000), então:
1 x 10 x 10 x 10 = 1000 →1m = 1000mm
Medidas de Área
Transformando 1m² (metro quadrado) em cm² (centímetro quadrado)
1º
passo:
transformar
m²
2º
passo:
transformar
dm²
Para ser mais prático, podemos multiplicar o m² por 100x100 (10 000) então:
1 x 100 x 100 = 10 000 → 1m² = 10 000cm²
em
em
dm²
cm²
Exemplo 1
Um muro com as seguintes medidas: 20 m de comprimento e 2 m de altura, foi construído com tijolos de
dimensões 20 cm de comprimento e 20 cm de altura. Quantos tijolos foram gastos na construção,
descartando a hipótese de desperdício?
Calculando a área do muro e a área do tijolo:
Área do muro
Área do tijolo
20m x 2m = 40 m²
20 cm x 20 cm = 400 cm²
Observamos que a área do muro e a do tijolo estão em unidades diferentes, então devemos utilizar
a tabela de conversões no intuito de igualar as unidades de medidas, podemos escolher entre as
seguintes transformações:
m² em cm²
ou
cm² em m²
Vamos transformar m² em cm²:
40 x 100 x 100 = 400.000 cm²
Para descobrir quantos tijolos foram gastos, basta dividirmos a área do muro em cm² pela área de
um tijolo também em cm²:
400.000 cm² / 400 cm² = 1.000 tijolos.
Resposta: Foram gastos 1000 tijolos na construção do muro.
Exemplo 2
Pedro deseja colocar cerâmica na área de lazer de sua casa, que possui 9 m de comprimento por 6 m de
largura. Se forem usadas cerâmicas quadradas com lado medindo 100 cm, quantas serão gastas?
Calculando a área da área de lazer e a área da cerâmica:
Área da área de lazer em m²
9m x 6m = 54m²
Área da cerâmica em cm²
100cm x 100cm = 10.000 cm²
Transformando cm² em m², temos:
10.000 / 100 / 100 = 1 m²
Para descobrir quantas cerâmicas serão utilizadas, basta dividirmos a área da área de lazer em m²
pela área de uma cerâmica também em m²:
54m² / 1m² = 54 ceramicas
1
Prof. José dos Santos Garcia Neto
Resposta: Serão utilizadas 54 cerâmicas na área de lazer da casa de Pedro
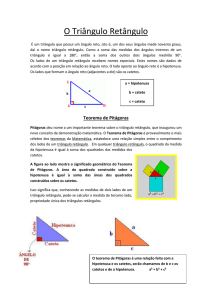
Teorema de Pitágoras
O teorema de Pitágoras é uma relação
relação matematica entre os comprimentos dos lados de qualquer triangulo
retângulo. Na geometria euclidiana, o teorema afirma que:
“Em
Em qualquer triângulo retângulo, o quadrado do comprimento da hipotenusa é igual à soma dos
quadrados dos comprimentos dos catetos.”
Por definição, a hipotenusa é o lado oposto ao angulo reto, e os catetos são os dois lados que o
formam. O enunciado anterior relaciona comprimentos, mas o teorema também pode ser enunciado como
uma relação entre áreas:
“Em qualquer triângulo retângulo,
etângulo, a área do quadrado cujo lado é a hipotenusa é igual à soma das áreas
dos quadrados cujos lados são os catetos.
Para ambos os enunciados, pode-se
pode
equacionar:
ou √ onde: c representa o comprimento da hipotenusa,
a e b representam os comprimentos dos catetos,
O teorema de Pitágoras leva o nome do matematico grego Pitágoras (570 a - 495 a.C.), que
tradicionalmente é creditado pela sua descoberta e demonstração embora seja frequentemente
argumentado que o conhecimento do teorema seja anterior a ele (há muitas evidências
evidências de que matmaticos
babilonicos conheciam algoritimos para calcular os lados em casos específicos, mas não se sabe se
conheciam um algoritmo tão geral quanto o teorema de Pitágoras).
O teorema de Pitágoras é um caso particular da lei dos cossenos do matematico persa Ghiyath al-Kashi
al
(1380 – 1429), que permite o cálculo do comprimento do terceiro lado de qualquer triangulo, , dados os
comprimentos de dois lados e a medida de algum dos três angulos.
O teorema de Pitágoras: a soma das áreas dos quadrados
quadrados construídos sobre os catetos (a
( e b) equivale à
áread do quadrado construído sobre a hipotenuza (c).
(
Trigonometria do triangulo retangulo
Um triângulo é uma figura geométrica plana, constituída por três lados e três ângulos internos. Esses
ângulos, tradicionalmente, são medidos numa unidade de medida, denominada grau e, cada um deles tem
o
o
o
medida entre 0 e 180 , de modo que, em qualquer triângulo, a soma dessas medidas é 180 .
Em um triangulo retângulo definimos as chamadas razões trigonométricas que são relações entre os lados
do triângulo e que têm a propriedade de determinar a medida dos ângulos do triângulo, uma vez que seus
lados sejam conhecidos.
2
Prof. José dos Santos Garcia Neto
Em um triangulo é dito retângulo quando um de seus ângulos é reto, isto é, tem mediada de 90º. Os outros
dois ângulos são agudos, dado um segmento ,, indicamos o comprimento de por AB, onde
AB=med(
).
No triângulo retângulo ABC, consideremos, por exemplo, o ângulo que tem vértice em B, cuja medida x, em
graus, é um número real que está no intervalo 0,90 Entre os lados do triângulo podemos estabelecer as
seguintes razões:
Seno: Seno de x é a razão entre o comprimento do cateto oposto ao ângulo e o comprimento da hipotenusa
do triângulo. Então temos:
AC
CatetoOposto
senx BC
Hipotenusa
Cosseno: Cosseno de x é a razão entre o comprimento do cateto adjacente ao ângulo e o comprimento da
hipotenusa do triângulo. Então temos:
)*+*&
,-+.*+
&'( )
/01&*+.2'
Tangente: Tangente de x é a razão entre os comprimentos do cateto oposto e do cateto adjacente ao
ângulo. Então temos:
)
)*+*&41&'*&
*3( )*+*&
,-+.*+
Representação gráfica do Seno, Cosseno e Tangente.
Interpolação
Se uma tabela apresenta seus valores de entrada com espaçamentos variáveis, tornando-se
tornando
difícil a
obtenção de um valor desejado, podemos aplicar o método da interpolação linear simples.
Interpolação Simples
Vamos supor que seja necessário conhecer o sen de 52º. Na tabela temos o sen 45º e o sen de 60º, mas
não temos o valor do sen 52º. Assim, deveremos proceder à interpolação linear.
Temos como valores conhecidos mais próximos ao angulo desejado:
seno 45º ----
√
√
---- 0,707
seno 60º ------- 0,866
Após a localização destes valores montamos a tabela abaixo
(A) 45º ---------- (P) 0,707
(B) 52º ---------- (Q) x (desejamos saber)
(C) 60º ---------- (R) 0,866
Equacionando para
ra generalizar o procedimento:
5
675
5
685
Substituindo os valores conhecidos na equação:
60 : 455
0,866 : 0,7075
∴
60 : 525
0,866 : (5
15
0,159
∴
∴
8
0,866 : (5
∴ 15. 0,866 : (5 8. 0,159 ∴
3
Prof. José dos Santos Garcia Neto
∴ 12,990 : 15( 1,272 ∴
1,272 : 12,990
∴ :( ∴
15
∴ :( :0,781 ∴
∴ ( 0,781 ∴
∴sen 45º = 0,781.
Se efetuarmos a operação em uma calculadora obteremos sen 52º = 0,788, muito próximo do calculado
pela interpolação simples, portando o valor calculado pode ser considerado para cálculos que utilizam o
angulo de 52º.
Arredondamento
Um número é arredondado para outro, com o número de algarismos significativos desejados, pelo
cancelamento de um ou mais algarismos da direita para a esquerda.
Duas regras podem ser utilizadas neste caso:
1-Quando o algarismo suprimido é menor do que 5, o imediatamente anterior permanece igual.
2-Quando o algarismo suprimido é maior ou igual a 5, o imediatamente anterior é acrescido de uma
unidade.
Exemplos:
a
Arredondar na 2 casa após a virgula:
L = 2,143 m (antes) ⇒ L = 2,14 m (depois)
a
Arredondar na 3 casa após a virgula:
L = 0,0506 m (antes) ⇒ L = 0,051 m (depois)
a
Arredondar na 1 casa após a virgula:
L = 0,12983 m (antes) ⇒ L = 0,1 m (depois)
a
Arredondar para um numero inteiro (0 casa após a virgula):
L = 1,55 m (antes) ⇒ L = 2 m (depois)
Referencias Bibliográficas:
http://pt.wikipedia.org/wiki/Teorema_de_Pit%C3%A1goras consultado em 22/11/13
http://ecalculo.if.usp.br/funcoes/trigonometricas/rz_trigo_triret.htm/rz_trigo_triret.htm consultado em 22/11/13
http://ecalculo.if.usp.br/funcoes/trigonometricas/rz_trigo_triret.htm/rz_trigo_triret.htm consultado em 22/11/13
http://www2.fc.unesp.br/~malvezzi/downloads/Ensino/Disciplinas/LabFisI_Eng/ApostilaTeoriaDosErros.pdf
consultado em 22/11/13
4
Prof. José dos Santos Garcia Neto