Mαtεmaticaηdθ

Mtmaticad
Geometria
Geometria Plana – Polígonos e circunferências – Lista 01
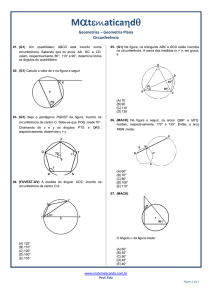
01. (FAAP) A medida mais próxima de cada ângulo externo
do heptágono regular da moeda de R$ 0,25 é:
(A) 60º.
(B) 45º.
(C) 36º.
(D) 83º.
(E) 51º.
05. (MACKENZIE) As medidas dos ângulos assinalados na
figura a seguir formam uma progressão aritmética. Então,
necessariamente, um deles sempre mede:
(A) 108º.
(B) 104º.
(C) 100º.
(D) 86º.
(E) 72º.
02. (FUVEST) Dois ângulos internos de um polígono convexo
medem 130° cada um e os demais ângulos internos
medem 128° cada um. O número de lados do polígono é:
06. (UNITAU) O polígono regular convexo em que o número
de lados é igual ao número de diagonais é o:
(A) 6.
(B) 7.
(C) 13.
(D) 16.
(E) 17.
(A) dodecágono.
(B) pentágono.
(C) decágono.
(D) hexágono.
(E) heptágono.
03. O polígono regular cujo ângulo interno mede o triplo do
ângulo externo é o:
(A) pentágono.
(B) hexágono.
(C) octógono.
(D) decágono.
(E) dodecágono.
04. (ITA) Considere
convexos:
07. (FATEC) Na figura a seguir, o triângulo APB está inscrito
na circunferência de centro C.
as
afirmações
sobre
polígonos
I.
Existe apenas um polígono cujo número de diagonais
coincide com o número de lados.
II. Não existe polígono cujo número de diagonais seja o
quádruplo do número de lados.
III. Se a razão entre o número de diagonais e o de lados
de um polígono é um número natural, então o número
de lados do polígono é ímpar.
(A) Todas as afirmações são verdadeiras.
(B) Apenas I e III são verdadeiras.
(C) Apenas I é verdadeira.
(D) Apenas III é verdadeira.
(E) Apenas II e III são verdadeiras.
Se os ângulos assinalados têm as medidas indicadas,
então x é igual a:
(A) 23º45'.
(B) 30º.
(C) 60º.
(D) 62º30'.
(E) 66º15'.
www.matematicando.com.br
Prof. Edu
Página 1 de 4
Mtmaticad
08. (FUVEST) Os pontos A, B e C pertencem a uma
circunferência  e AC é lado de um polígono regular
$ mede 18º
inscrito em . Sabendo-se que o ângulo ABC
11. (MACKENZIE) Na figura a seguir, os arcos QMP e MTQ
medem, respectivamente, 170º e 130º. Então, o arco
MSN mede:
podemos concluir que o número de lados do polígono é
igual a:
(A) 60º.
(B) 70º.
(C) 80º.
(D) 100º.
(E) 110º.
(A) 5.
(B) 6.
(C) 7.
(D) 10.
(E) 12.
09. (FUVEST-GV) A medida do ângulo ADC inscrito na
circunferência de centro O é:
(A) 125º.
(B) 110º.
(C) 120º.
(D) 100º.
(E) 135º.
12. (UFMG) Observe a figura.
Nessa figura, BD é um diâmetro da circunferência circunscrita
$
$
ao triângulo ABC, e os ângulos ABD
e AED
medem,
respectivamente, 20º e 85º.
10. (G1) (FUVEST 84) Um arco de circunferência mede 300º,
e seu comprimento é 2 km. Qual o número inteiro mais
próximo da medida do raio em metros?
(A) 157.
(B) 284.
(C) 382.
(D) 628.
(E) 764.
$ mede:
Assim sendo, o ângulo CBD
(A) 25º.
(B) 35º.
(C) 30º.
(D) 40º.
www.matematicando.com.br
Prof. Edu
Página 2 de 4
Mtmaticad
13. (UFMG) Observe a figura.
(A) 2.
(B)
(C)
Nessa figura, AB é um diâmetro do círculo de centro O e
µ mede 15º.
raio 2 e o ângulo PAB
Nesse caso, a distância do ponto P à reta AB é de:
(A)
(E)
 3 .
2
(B) 1.
(C) 2 .
(D)
(D)
1 2 3  .
2  3  .
2  2 3  .
3  3  .
17. (PUC) O ângulo x, na figura a seguir, mede:
3 .
14. (UFSCAR) Um polígono regular com exatamente 35
diagonais tem:
(A) 6 lados.
(B) 9 lados.
(C) 10 lados.
(D) 12 lados.
(E) 20 lados.
15. (UNESP) A distância entre dois lados paralelos de um
hexágono regular é igual a 2 3 cm. A medida do lado
desse hexágono, em centímetros, é:
(A) 3 .
(B) 2.
(C) 2,5.
(D) 3.
(E) 4.
(A) 60º.
(B) 80º.
(C) 90º.
(D) 100º.
(E) 120º.
18. (Escola Técnica Federal-RJ) Quando o comprimento de
uma circunferência aumenta de 8 cm para 14 cm o raio
da circunferência aumenta de:
A)
16. (FUVEST) Numa circunferência, c1 é o comprimento do

arco de
radianos e c2 é o comprimento da secante
6
determinada por este arco, como ilustrado na figura a
c

seguir. Então, a razão 1 é igual a
multiplicado por:
c2
6
B)
C)
D)
E)

cm.
6
3
cm.


cm.
3
1,5cm.
3cm.
www.matematicando.com.br
Prof. Edu
Página 3 de 4
Mtmaticad
19. (ESPM 96) Uma circunferência está inscrita em um
quadrado cuja diagonal mede 20 cm. O comprimento da
circunferência é:
10. (C)
11. (A)
(A)  2 cm.
(B) 5  2 cm.
(C) 10  2 cm.
12. (A)
(D) 20  2 cm.
(E) 30  2 cm.
20. (UFV) Aumentando-se 1 m no raio r de uma
circunferência, o comprimento e a área, respectivamente,
aumentam:
2
(A) 2 m e 2 (r + 1) m .
2
(B) 2 m e (2r + 1) m .
2
2
(C) 2 m e (2r + 1) m .
2
2
(D) 2 m e (2r + 1) m .
2
2
(E) 2 m e (r + 1) m .
GABARITO
01. (E)
02. (B)
03. (C)
04. (B)
13. (B)
14. (C)
15. (B)
16. (C)
17. (B)
18. (B)
19. (C)
20. (B)
05. (A)
06. (B)
07. (E)
08. (D)
09. (A)
www.matematicando.com.br
Prof. Edu
Página 4 de 4