laboratório 05

(
(
(
(
(
) Prova
( ) Prova Semestral
) Exercícios
( ) Prova Modular
) Segunda Chamada
( ) Exame Final
) Prática de Laboratório
) Aproveitamento Extraordinário de Estudos
Disciplina:
Professor:
Turma:
Data:
Nota:
Aluno (a):
Experiência 05: TRANSITÓRIO DE SISTEMAS RC
1. Objetivo Geral
Verificar as características do comportamento de um sistema de primeira ordem para
uma entrada do tipo degrau.
2. Objetivo Específico
Verificar na prática o tipo de resposta de um sistema de primeira ordem;
Verificar experimentalmente a carga e descarga de um capacitor;
Projetar resistor para obter determinado comportamento.
3. RESUMO TEÓRICO
O capacitor é um componente que armazena energia na forma de campo elétrico.
1
Os capacitores se apresentam numa grande variedade de tamanhos e formas.
Entretanto, os elementos básicos de qualquer capacitor são dois condutores isolados de
formato arbitrário. Chamamos tais condutores de placas, qualquer que seja sua
geometria. A figura 01 mostra um arranjo chamado de capacitor de placas paralelas.
Figura 01 – Capacitor de Placas Paralelas
Fonte: http://www.bairrospd.kit.net/componentes/capacitor/CapBasico/CapBasico.html
1
HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de Física 3: Eletromagnetismo. Rio de Janeiro: LTC,
1980. 322p.
RQ 0501 Rev. 13
Página 1 de 9
Portanto um capacitor é um componente composto de placas separadas por um
material dielétrico (isolante). A capacitância (C) é uma constante que define a capacidade
do capacitor armanezar energia por unidade de tensão. Por definição:
C=
q (t )
; onde q = carga elétrica. Unidade: Coulomb (C)
V (t )
(01)
V = tensão. Unidade: Volt (V)
Logo a unidade da capacitância é coulomb por volt, que também é denominada de
farad (F). O farad é uma unidade muito grande, portanto na prática depara-se usualmente
com microfarad (µF = 10-6 F), nanofarad (nF = 10-9 F) e o picofarad (pF = 10-12 F). Existem
vários tipos de capacitores, o que muda basicamente de um para o outro é o valor de
capacitância e a tensão de isolação.
A codificação dos capacitores é bem variada, depende do tipo e do tamanho deste
componente. Há a codificação em cores, conforme mostra a figura 02, e a codificação em
letras. Para maiores informações sobre este assunto recomenda-se a leitura de livros
técnicos.
Figura 02 – Código de Cores dos Capacitores
Circuitos elétricos do tipo RC (resistor e capacitor) funcionam como sistemas de
primeira ordem contínuos, pois a lei que rege o comportamento destes é descrito
matematicamente pela seguinte equação:
RQ 0501 Rev. 13
Página 2 de 9
a1
dy (t )
+ a0 y (t ) = f ( x) ; onde y (t ) = saída no tempo
dt
(02)
f (x) = função entrada
a1 , a0 = constantes
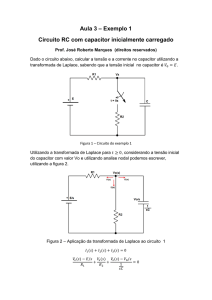
Um esquema de um circuito RC é mostrado na figura 03, onde a saída é a tensão
no capacitor (Vc) e a entrada é uma fonte de tensão constante V.
Figura 03 – Circuito RC
Aplicando a Lei de Kirchhoff da tensão para esta malha, tem-se:
V (t ) = Vr (t ) + VC (t ) ∴ V (t ) = i (t ) * R + VC (t )
Como i (t ) =
V (t ) = RC
(03)
dq (t )
e q (t ) = CV (t ) , conforme equação 01, obtém-se:
dt
dVc (t )
+ VC (t )
dt
(04)
A equação diferencial acima rege o comportamento de sistemas de primeira ordem
do tipo RC. Esta descreve a curva de carga e descarga do capacitor.
3.1 Carga do Capacitor
Neste caso, supõe-se que o capacitor encontra-se inicialmente descarregado, ou
seja, Vc(t0) = 0 V e que em t0 = 0 (tempo inicial) a chave “S” é fechada instantaneamente.
Neste instante a corrente inicial do circuito é máxima e começa o processo de carga do
capacitor com um aumento gradativo de Vc dado pela constante de tempo do circuito.
Conforme a tensão Vc aumenta, a corrente do circuito diminui até chegar ao valor zero.
Nesta situação o capacitor encontra-se totalmente carregado.
RQ 0501 Rev. 13
Página 3 de 9
O comportamento das variáveis tensão no capacitor e corrente do circuito é dado
pela resolução da equação 04. É possível provar que:
(t −t0 )


−

Vc (t ) = V * 1 − e RC  ; onde a constante de tempo (τ) do circuito é R*C.




i (t ) =
(05)
(t −t )
V  − RC0 
* e

R 

(06)
3.2 Descarga do Capacitor
Neste caso, com base na figura 03, supõe-se que o capacitor encontra-se
inicialmente carregado, ou seja, Vc(t0) = Vcmáx e que a fonte de tensão constante é igual a
0 V, o que significa que a mesma foi curto-circuitada. Em t0 = 0 (tempo inicial) a chave “S”
é fechada instantaneamente. Neste instante inicia o processo de descarga do capacitor
com um decréscimo gradativo de Vc dado pela constante de tempo do circuito.
O comportamento da tensão no capacitor é dado pela resolução da equação 04,
fazendo f(x)=0. Desta forma:
Vc (t ) = Vcmáx * e
−
(t −t0 )
RC
; onde a constante de tempo (τ) do circuito é R*C.
(07)
A curva de descarga do capacitor é mostrada na figura 04, esta obtida através da
equação 07.
Figura 04 – Curvas de Carga e Descarga do Circuito RC
A curva do comportamento da corrente do circuito (figura da direita) e a curva de carga
do capacitor (figura da esquerda) são mostradas na figura 04, ambas obtidas através das
equações 05 e 06.
RQ 0501 Rev. 13
Página 4 de 9
4. Lista de Material e Equipamentos
Gerador de Sinais;
Potenciômetro Linear de 10kΩ;
Osciloscópio (20MHz);
Capacitor de 47nF;
5. Procedimento
Dado o circuito de primeira ordem abaixo:
Figura 06 – Circuito da Experiência
5.1 Calcule o valor da resistência para que a constante de tempo seja igual a 5 µs.
RQ 0501 Rev. 13
Página 5 de 9
5.2 Monte o circuito da figura 6 e ajuste o potenciômetro com o valor de resistência
encontrado no item 5.1. Ajuste o gerador de sinais com uma onda quadrada de 4 volts de
amplitude e freqüência adequada. Com o osciloscópio monitore a tensão no capacitor.
Desenhe a forma de onda na saída do circuito.
Vp (tensão de pico) =
______________________V
Vpp (tensão pico a pico) =
______________________V
Vrms (tensão eficaz) =
_______________________V
T (período) =
_______________________s
f (frequência) =
_______________________Hz
Encontre a equação matemática teórica que descreve o comportamento do sistema
nesta situação (carga e descarga), conforme equações 05 e 07.
RQ 0501 Rev. 13
Página 6 de 9
5.3 Monte o circuito da figura 6, porém coloque as ponteiras do osciloscópio no
resistor. Ajuste o gerador de sinais com uma onda quadrada de 4 volts de amplitude e
freqüência adequada. Desenhe a forma de onda na saída do circuito.
Vp (tensão de pico) =
______________________V
Vpp (tensão pico a pico) =
______________________V
Vrms (tensão eficaz) =
_______________________V
T (período) =
_______________________s
f (frequência) =
_______________________Hz
Encontre a equação matemática teórica que descreve o comportamento da
corrente do circuito nesta situação (carga e descarga).
RQ 0501 Rev. 13
Página 7 de 9
5.4 Monte o circuito da figura 6 e ajuste o potenciômetro com a metado do valor de
resistência encontrado no item 5.1. Ajuste o gerador de sinais com uma onda quadrada
de 4 volts de amplitude e freqüência adequada. Com o osciloscópio monitore a tensão no
capacitor.
Desenhe a forma de onda na saída do circuito.
RQ 0501 Rev. 13
Página 8 de 9
Vp (tensão de pico) =
______________________V
Vpp (tensão pico a pico) =
______________________V
Vrms (tensão eficaz) =
_______________________V
T (período) =
_______________________s
f (frequência) =
_______________________Hz
Qual(is) é(são) a(s) diferença(s) entre este comportamento e o comportamento
registrado no item 5.2? Descreva em detalhes.
6. REFLEXÕES
RQ 0501 Rev. 13
Página 9 de 9