X - BIOCOMP IFF

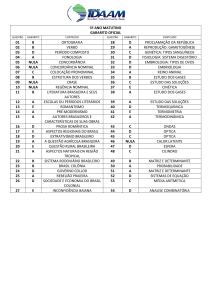
Bioestatística e Computação I
Problema
●
Inferência por Teste de Hipótese
X → Altura de indivíduos com 12 a 40 anos
que sofrem de síndrome alcoólica fetal.
●
Deseja-se inferir se a média µ dessa população
é significativamente diferente da média da
população de mesma faixa etária que não sofre
de síndrome alcoólica fetal µ0=160 cm.
●
A distribuição de X é aproximadamente normal
com média µ desconhecida.
●
A partir de uma amostra aleatória de 31
indivíduos a média µ foi estimada por
x =147,4 cm.
●
Há evidência de que
Maria Virginia P Dutra
Eloane G Ramos
Vania Matos Fonseca
Pós Graduação em Saúde da Mulher e da Criança
IFF – FIOCRUZ
Baseado nas aulas de M. Pagano e Gravreau e Geraldo Marcelo da Cunha
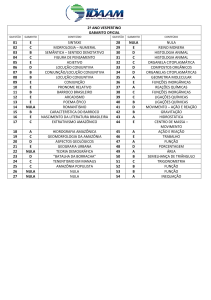
Teste de Hipótese
Teste de Hipótese
●
Permite afirmar, com um certo grau de
confiança, que uma determinada hipótese
numérica é válida.
µ≠µ0?
Para cada tipo de hipótese há um tipo de
teste
●
Hipótese sobre uma média
●
Hipótese sobre duas médias
●
Hipótese sobre proporções
●
Hipótese sobre variâncias
●
...
Teste de Hipótese sobre 1 Média
Teste de Hipótese sobre 1 Média
●
●
Outros exemplos
●
A média de nível sérico de colesterol para a
população de homens hipertensos e fumantes é
significativamente diferente da população em
geral?
●
O volume médio de glóbulos vermelhos é menor
do que o normal na população que se encontra
em insegurança alimentar moderada ou grave?
●
A média do ângulo de fase da bioimpedância de
crianças sépticas é diferente da média das
crianças normais?
Estamos interessados em afirmar que a média
de uma população µ, estimada a partir de uma
amostra, é significativamente diferente de um
valor pré-estabelecido µ0.
Teste de Hipótese sobre 1 média
●
A média para uma população µ, estimada a
partir de uma amostra, é significativamente
diferente de um determinado valor µ0?
●
É necessária uma prova dessa diferença.
●
Até que se prove o contrário, deve-se
presumir a igualdade.
●
A hipótese que se deseja provar é como se
fosse um crime.
●
Até que se prove o contrário o réu é inocente.
Teste de Hipótese sobre 1 média
1.Para provar que uma
média µ é diferente
de um determinado
valor µ0 começamos
afirmando que ela é
igual.
Teste de Hipótese sobre 1 média
●
●
Hipótese nula
●
H0
●
Hipótese da igualdade
●
H0:
Essa é a hipótese
que queremos
rejeitar.
µ = µ0
Hipótese alternativa
●
HA
●
Hipótese da desigualdade
●
HA:
µ ≠ µ0
Teste de Hipótese sobre 1 média
2.Estabelece-se o nível de significância do teste, a
probabilidade de errar se a hipótese nula for
verdadeira.
3.Retira-se uma amostra aleatória da população de
interesse e estima-se a média µ a partir da média
amostral 
x.
4.Há evidência significativa de que µ seja diferente
de µ0?
5.Se sim, rejeita-se a hipótese nula e aceita-se a
hipótese alternativa.
6.Se não, só podemos afirmar que não há evidência
da diferença.
Teste de Hipótese sobre 1 média
●
Portanto, o interesse em se
Teste de Hipótese sobre 1 média
●
Ao pressupor que H0 é verdadeira, pode-se
realizar um teste de hipótese é
supor também a respeito da distribuição de
.
probabilidade de X
sempre rejeitar a hipótese nula
 ~ 0,  
Se H 0 é verdadeira: X
n
●
(H0) em favor da hipótese
alternativa (HA).
●
A partir daí podemos estabelecer a
 assumir um valor tão ou
probabilidade de X
mais extremo que o observado e decidir se é
realmente plausível que H0 seja verdadeira.
Se partíssemos de HA, não teríamos uma
distribuição de probabilidade definida.
Teste de Hipótese sobre 1 média
●
●
●
Teste bilateral
●
H0:
µ = µ0
●
HA:
µ ≠ µ0
●
Teste unilateral
●
H0:
µ ≤ µ0
●
H0:
µ ≥ µ0
●
HA:
µ > µ0
●
HA:
µ < µ0
Vamos estabelecer que queremos rejeitar a
hipótese nula com uma probabilidade de
erro de 5%.
●
Nível de significância
●
α = 0,05
●
O pesquisador escolhe o α dependendo da
precisão que deseja, das evidências na
literatura, …
Deseja-se inferir se a média de altura da
população com 12 a 40 anos que sofre de
síndrome alcoólica fetal µ é significativamente diferente da média da população de
mesma faixa etária que não possui a
síndrome µ0=160cm. Considere σ = 6cm.
●
Hipótese nula
–
Juntas, as duas hipóteses devem cobrir
todos os valores possíveis para a média µ.
Teste de Hipótese sobre 1 média
●
Teste de Hipótese sobre 1 média
●
H0:
µ = µ0=160cm
Hipótese alternativa
–
HA:
µ ≠ µ0 ou µ ≠ 160cm (teste bilateral)
Teste de Hipótese sobre 1 média
●
Selecionou-se uma amostra aleatória de 31
indivíduos da população de interesse,
obtendo-se uma altura média de 147,4 cm.
µ seja
●
Há evidência significativa de que
diferente de µ0=160cm?
●
Com um nível de significância α de 5%, que
valores de 
x nos levariam a rejeitar a hipótese
nula?
Teste de Hipótese sobre 1 média
●
Teste de Hipótese sobre 1 média
Distribuição
Normal Padrão
Se H0 fosse verdadeira
=0=160cm
 ~ 0,  
X
n
 −0 X
X
 −160
Z=
=
/n
6/  31
α/2 = 0,025
-5
-4
-3
-2
0
1
-1,96
2
3
4
1,96
5
α=0,05 → P(Z<-z ou Z>z) = 0,05 → z = ± 1,96
●
Região de Rejeição: Z<-1,96 ou Z>1,96
●
Para um determinado 
x, se Z estiver na região
de rejeição, estaremos observando um evento
muito improvável (probabilidade < 5%).
●
Nesse caso, rejeitaríamos a hipótese nula.
Outra forma de concluir o teste
●
p-valor
–
Probabilidade de observar uma média amostral tão
ou mais extrema que o valor observado, caso H0
fosse verdadeira.
●
p = P(Z<-11,7 ou Z>+11,7) = ?
●
Pela tabela A.3 p<0,001 ou p≈0
●
Como p<α, rejeita-se a hipótese nula.
●
z
●
Teste de Hipótese sobre 1 média
●
Para a amostra selecionada
0,025
0,95
-1
●
0,025
0,95
0,025
x =147,4
x −160 147,4−160
-5 -4 -3 -2 -1 0 1 2 3 4 5
Z=
=
=−11,7
z
1,96
-1,96
6/  31
6/  31
Como Z está na região de rejeição, há evidência
de que H0 seja falsa.
●
Rejeitamos a hipótese nula de que
µ=µ0=160cm.
●
Podemos afirmar, com 5% de chance de erro,
que a média de altura µ da população com
síndrome alcoólica fetal é significativamente
diferente da média da população em geral µ0.
Teste de Hipótese sobre 1 média
●
Deseja-se testar se a média µ do nível
sérico de colesterol da população de
homens hipertensos e fumantes é
significativamente diferente da população
de homens em geral µ0=211mg/100ml.
●
●
O nível de significância desejado é α = 5% e o
desvio-padrão da população em geral é σ =
46mg/100ml.
Seleciona-se aleatoriamente uma amostra de 12
homens hipertensos fumantes e mede-se um
nível médio de colesterol de 217mg/100ml.
Teste de Hipótese sobre 1 média
●
α = 0,05
Solução
0=211, =46, =0,05 , n=12, x =217
●
●
●
Região de rejeição
Se H0 é verdadeira
Hipóteses
–
H0:
µ = µ0=211
–
HA:
µ ≠ µ0 ou µ ≠ 211
Região de rejeição para
–
α=5%
Padronização
Z<-1,96 ou Z>+1,96
Para 
x =217
x −0 217−211
Z=
=
=0,45
 /n
46/  12
µ=211
Teste de Hipótese sobre 1 média
●
Teste de Hipótese sobre 1 média
Z está fora da região de rejeição
217
x
-1.96
Teste de Hipótese sobre 1 média
●
Conclusão pelo p-valor
●
Não rejeita-se a hipótese nula
●
Z = 0,45
●
Não há evidência significativa de que a média µ
do nível sérico de colesterol da população de
homens fumantes e hipertensos seja diferente
da média da população de homens em geral µ0.
●
p = P(Z<-0,45 ou Z>+0,45)
●
●
Mas também não há prova de que seja igual.
Não se pode afirmar que
µ = µ 0.
–
Pode ser que µ seja igual a outro valor.
–
H0 nunca é aceita, apenas HA não é rejeitada.
z = 0 0.45 1.96
–
teste bilateral
●
Pela tabela A.3, p = 2 x 0,326 = 0,652
●
p>α
●
Não rejeita-se a hipótese nula.
z
Teste de Hipótese sobre 1 média
●
Teste unilateral
●
●
Queremos determinar se o nível médio de
hemoglobina µ para a pop. de crianças de até 6
anos expostas a altos níveis de chumbo é
menor do que a média para crianças não
expostas, pois não é razoável imaginar que
seria maior.
Teste de Hipótese unilateral
●
Solução
0=12,29 , =0,85 , =0,05 , n=74, x =10,6
●
●
Considere α=5%, a média p/ não expostos
µ =12,29 g/100ml e σ=0,85 g/100ml.
●
Z está na região de rejeição
●
●
●
Uma amostra aleatória de 74 crianças expostas
a altos níveis de chumbo apresentou nível
médio de hemoglobina de 10,6 g/100ml.
Teste de Hipótese unilateral
–
H0:
µ ≥ 12,29
–
HA:
µ < 12,29
α=5%
Z<-1,645
α = 0,05
Para 
x =10,6
x −0 10,6−12,29
Z=
=
=−17,1
 /n
0,85/  74
-5
-4
-3
0,95
-2
●
Teste bilateral
Z = -17,1
●
p = P(Z<-17,1) → teste unilateral
-5
●
Rejeita-se a hipótese nula.
-4
-3
-2
-1
0
1
-z
●
p<α
1
2
3
Deve ser
decidido
antes de
selecionar
amostra
●
Teste
bilateral é
sempre
mais
conservador
p
Pela tabela A.3, p ≈ 0
●
0
●
Rejeita-se a hipótese nula.
●
-1
-1,645
Teste de Hipótese para uma média
Conclusão pelo p-valor
●
Distribuição
Normal Padrão
Região de rejeição para
–
0
●
Hipóteses p/ teste unilateral
2
3
4
5
z
Teste unilateral
–
p
-5
-4
-3
-2
-1
0
1
z
2
3
4
5
p 2x maior
4
Teste de Hipótese para uma média
●
Teste Z
●
●
Solução
0 =?
=?
n=?
x =?
desvio-padrão s=?
●
A população de bebês normais possui nível
médio de alumínio no plasma de 4,13µg/l.
●
Ao selecionar aleatoriamente uma amostra
de 10 bebês que recebem antiácidos com
alumínio, obteve-se uma média de 37,2µg/l
e um desvio-padrão de 7,13µg/l.
●
A um nível de significância de 5%, há
evidências de que a população que recebe
antiácidos possua nível médio de alumínio
plasmático diferente da população que não
recebe?
σ desconhecido
Teste t
●
●
σ conhecido
Teste t
●
Teste t
Teste t
●
Solução
0=4,13 , =0,05 , n=10, x =37,2 , s=7,13
●
●
Hipóteses p/ teste bilateral
–
H0:
µ = 4,13
–
HA:
µ ≠ 4,13
Região de rejeição para t9 e
–
Teste bilateral ou unilateral?
●
α=5% (tabela A.4)
t<-2,262 ou t>2,262
x =37,2
Para 
x −0 37,2−4,13
t=
=
=14,67
s /  n 7,13/  10
Distr. t com 9 gl
0,025
-5 -4 -3 -2 -1
-2,262
0,025
0,95
0
1
2
3
2,262
4
5
z
Teste t
●
t está na região de rejeição
●
●
Resumindo
●
Rejeita-se a hipótese nula.
Conclusão pelo p-valor
Desvio
padrão
●
t = 14,67
●
p = P(t<-14,67 ou t>14,67) - teste bilateral
●
Pela tabela A.4, p < (2*0,0005), p<0,001 ≈ 0
●
p<α
●
populacional
σ
Rejeita-se a hipótese nula.
Conclusão do
teste
 −0
X
/n
bilateral
Região
de
rejeição
|Z|>zα/2
unilateral
|Z|>zα
 −0
X
bilateral
|t|>tn-1,α/2
s/n
unilateral
|t|>tn-1,α
Estatística
Lateralidade
Teste
de teste
amostral
s
Tipos de Erro
●
Testes de hipótese para 1 média
Z
t
Z=
t=
Tipos de Erro
População
H0 verdadeira
H0 falsa
µ = µ0
µ ≠ µ0
Não rejeita H0
Correto
Rejeita H0
Erro tipo I
α
Conclusão do
teste
Erro tipo II
β
Correto
Erro tipo I
●
População
H0 verdadeira
H0 falsa
µ = µ0
µ ≠ µ0
Não rejeita H0
Correto
Erro tipo II - β
Rejeita H0
Erro tipo I - α
Correto
Erro tipo II
–
Não rejeitar H0 quando ela é falsa
–
Rejeitar H0 quando ela é verdadeira
–
P(Erro tipo II) = P(não rejeitar H0 | H0 falsa) = β
–
P(Erro tipo I) = P(Rejeitar H0 | H0 verdadeira) = α
–
Se H0 for falsa, β é a proporção de repetidos testes nos
–
Nível de significância
–
Ao repetir vários testes, se H0 for verdadeira, em 5%
deles concluiríamos erroneamente que H0 é falsa.
quais concluiríamos erroneamente que H0 é verdadeira.
–
Poder do teste = 1- β, propabilidade de acertar quando H0
é falsa
Teste de Hipótese e Intervalo de Confiança
●
●
Teste de Hipótese e Intervalo de Confiança
Nível sérico colesterol de fumantes e hipertensos
H 0 : =0=211, =46, =0,05 , n=12, x =217
●
Intervalo de confiança de 95% (1-α) para
●
–
→
–
Intervalo de confiança de 95% (1-α) para
–
P(-z < Z < +z) = 0,95
z = ± 1,96
→
–
IC95% =
x ±
z
1,96×46
=217±
=217±26,02= 190,98 ; 243,02 
n
 12
190,98
–
µ
Alumínio no plasma de bebês com antiácidos
H 0 : =0=4,13 , =0,05 , n=10, x =37,2 , s=7,13
µ =211
0
Como o IC95% inclui
µ0, não podemos rejeitar H0
P(-t < t9 < +t) = 0,95
t = ± 2,262
IC95% =
x ±
t
2,262×7,13
=37,2±
=37,2±5,1= 32,1 ; 42,3 
n
 10
µ =4,13
243,02
0
–
µ
Como o IC95% não inclui
chance de erro
32,1
42,3
µ0, rejeitamos H0 com 5% de