Representação digital

SEPS – REPRESENTAÇÃO DE Nºs DIGITAIS I


Representação binária inteira sem
sinal
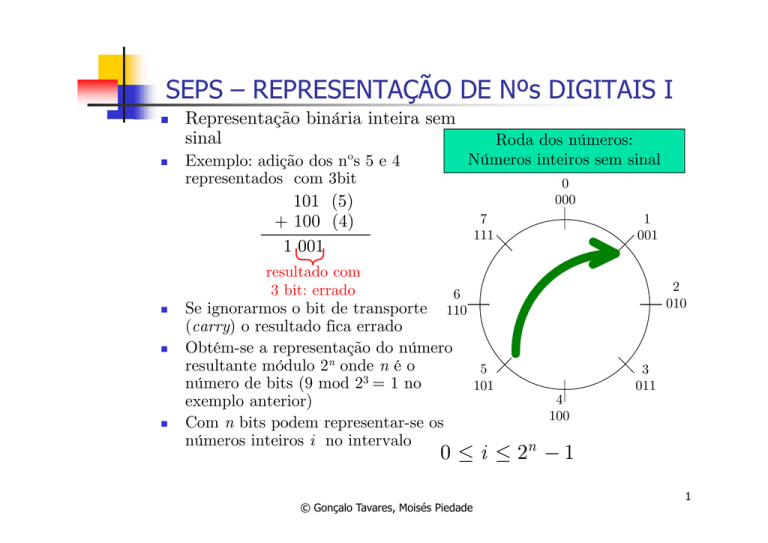
Exemplo: adição dos nºs 5 e 4
representados com 3bit
Roda dos números:
Números inteiros sem sinal
0
000
101 (5)
+ 100 (4)
1 001
resultado com
3 bit: errado



7
111
1
001
2
010
6
110
Se ignorarmos o bit de transporte
(carry) o resultado fica errado
Obtém-se a representação do número
resultante módulo 2n onde n é o
número de bits (9 mod 23 = 1 no
exemplo anterior)
Com n bits podem representar-se os
números inteiros i no intervalo
5
101
4
100
3
011
0 £ i £ 2n - 1
© Gonçalo Tavares, Moisés Piedade
1
SEPS – REPRESENTAÇÃO DE Nºs DIGITAIS II



Representação binária inteira com sinal:
números negativos representados em
complemento para 1
O MSB é o bit de sinal
Calcula-se pela equação
Números inteiros com sinal:
complemento para 1
0
000
1
001
X
111
i + icomplemento para 1 = 111
11


n bit
que equivale a considerar para
icomplemento para 1 o complemento lógico de i
(negação bitwise)
icomplemento para 1 = i

Com n bits podem representar-se os
números inteiros i no intervalo
-(2n -1 - 1) £ i £ 2n -1 - 1

2
010
-1
110
-2
101

-3
100
3
011
As palavras 000···000 e 111···111
representam o mesmo número, zero
A representação decimal é
ib = bn -1bn -2 b0  id = -bn -1(2n -1 - 1) +
© Gonçalo Tavares, Moisés Piedade
n -2
å bk 2k
k =0
2
SEPS – REPRESENTAÇÃO DE Nºs DIGITAIS III




Representação binária inteira com
sinal: números negativos
representados em complemento
para 2
É o sistema de representação mais
utilizado
O MSB é o bit de sinal
Calcula-se pela equação
Números inteiros com sinal:
complemento para 2
icomplemento para 2 = icomplemento para 1 + 1
0
000
-1
111
1
001
2
010
-2
110
= i +1

Com n bits podem representar-se os
números inteiros i no intervalo
-3
101
-2n -1 £ i £ 2n -1 - 1

A representação decimal é
-4
100
3
011
cuidado com
este número!
n -2
ib = bn -1bn -2 b0  id = -bn -1 2n -1 + å bk 2k
k =0
© Gonçalo Tavares, Moisés Piedade
3
SEPS – REPRESENTAÇÃO DE Nºs DIGITAIS IV

Adição de números com representação em complemento para 2:
A unidade aritmética em complemento para 2 permite realizar
somas que originam overflows sem que o resultado final esteja
errado, desde que este possa ser representado na gama dinâmica
da unidade aritmética
Exemplo: Cálculo da soma 3+6+1-4=6 com números de 4 bit que
permitem a representação entre [-7, 7] em complemento para 1 e
entre [-8, 7] em complemento para 2
0011
+ 0110
1001
+ 0001
1010
+ 1011
1 0101
(3)
(6)
(-6 ¹ 9)  errado!
(1)
(-5 ¹ 10)  errado!
(-4)
(5 ¹ 6)  errado!
Complemento para 1
0011
+ 0110
1001
+ 0001
1010
+ 1100
1 0110
(3)
(6)
(-7 ¹ 9)  errado!
(1)
(-6 ¹ 10)  errado!
(-4)
(6=6)  certo!
Complemento para 2
© Gonçalo Tavares, Moisés Piedade
4
SEPS – REPRESENTAÇÃO DE Nºs DIGITAIS V

Característica de uma ALU em complemento para 2:
Nº de saída
Modo de saturação
1
-1
0
1
Nº de entrada
-1



Em algumas aplicações a descontinuidade da característica de entrada/saída
pode provocar erros grosseiros e instabilidade na realização de sistemas, por
exemplo no cálculo de filtros. Nestes casos é preferível uma característica de
saturação (semelhante à dos amplificadores analógicos)
Por exemplo, no processador TMS320C2x as instruções assembly:
ROVM Reset overflow mode
SOVM Set overflow mode
permitem introduzir ou retirar o modo de saturação da ALU
A descontinuidade da característica permite realizar osciladores de relaxação
somando a uma variável (acumulador), repetidamente, um valor adequado:
short
rampa, delta=0x0100;
while(1) {
while(amostra_disponivel == 0); // espera intervalo de amostragem
amostra_disponivel = 0;
rampa += delta;
// calcula rampa
}
© Gonçalo Tavares, Moisés Piedade
5
SEPS – REPRESENTAÇÃO DE Nºs DIGITAIS VI



Multiplicação de números inteiros com sinal (complemento para 1 ou 2)
A multiplicação de dois números de n bit cada com sinal produz um
resultado com 2n bit dos quais dois são de sinal (1 bit de sinal repetido).
O resultado pode ser representado com apenas (2n-1) bit
Exemplo: quadrado do número mais negativo em complemento para 2
-2n -1 ´ (-2n -1 ) = 22n -2
que é representável em 2n-2 bit + 1 bit de sinal = 2n-1 bit

A multiplicação deve ser feita com extensão do sinal até aos 2n bit
Exemplo: Cálculo do produto -4´6=-24 com números de 4 bit
extensão de sinal
11111100 (-4)
´ 0110 (6)
00000000
1111100
111100
1 11101000 (-24)
1100 (-4)
´ 0110 (6)
0000
1100
1100
01001000 (78)
resultado errado!
necessário fazer
extensão de sinal
Carry
(bit de
transporte)
7 bit seriam
suficientes
Verificação
1101000
= 0010111
+
1
0011000 (24)
São gerados 2 bit
de sinal !
© Gonçalo Tavares, Moisés Piedade
6
SEPS – REPRESENTAÇÃO EM VÍRGULA FIXA I

Representação binária com parte inteira e fraccionária
s
eI-1

e1
e0
f0
f1

fF-1
ponto binário implícito
amplitude da parte
inteira (I bit)




parte fraccionária (F bit)
Representação fraccionária com vírgula fixa
A parte inteira é nula e os números (de n bit) são representados
apenas no intervalo -1 a +1 (aproximadamente, dependendo da
representação)
Obtém-se a partir de uma representação binária inteira com sinal
deslocando o ponto binário de n-1 bit para a esquerda (ou seja,
dividindo o número inteiro por 2n-1
Exemplo: (em complemento para 2)
1110 (-2)  dividindo por 2n -1= 8
© Gonçalo Tavares, Moisés Piedade
 1.110 (-0.25)
7
SEPS – REPRESENTAÇÃO EM VÍRGULA FIXA II



Nesta representação (com n bits) 1 bit é de sinal, não existem bits para
a parte inteira e n-1 bit ficam para a parte fraccionária:
Notação Qn-1
Em geral: palavras de n bit, com 1 bit de sinal, i = n–1-m para a
amplitude da parte inteira e m bit para a parte fraccionária:
Notação Qm
Em complemento para 2, permite representar números no intervalo:
-2i £ x £ 2i - 2-m
Exemplo: representar o número x = -0.123456789, com a máxima
precisão no TMS320C6416 (16 bit, vírgula fixa)
Como o processador é de 16 bit e |x| <1, a notação adequada é Q15, ou
seja m =15 e i=0. Para encontrar o valor decimal do número é necessário
multiplicá-lo por 2n-1 = 215:
15
xd = 2 x = -4045.43
Este valor deve ser arredondado para as unidades produzindo o valor final:
-4045 = -(0x0FCD)= 0xF032+1= 0xF033
© Gonçalo Tavares, Moisés Piedade
8
SEPS – REPRESENTAÇÃO EM VÍRGULA FIXA III

Na multiplicação de números fraccionários em vírgula fixa, é
necessário retirar os bits de sinal repetidos (o que não acontece
com a representação de números inteiros), caso contrário o
resultado vem errado
Exemplo: Cálculo do produto -0.50´0.75=-0.375 com números de 4 bit
representados em Q3 (maior precisão possível)
extensão de sinal
11111100 (-0.5)
´ 0110 (0.75)
00000000
1111100
111100
1 11101000 (-0.375)
têm de ser
guardados
estes 7 bit!
Carry
São gerados 2 bit
(bit de
de sinal !
transporte)
Verificação
1101000
= 0010111
+
1
0011000 (0.375)
(ver o exemplo de multiplicação de dois números inteiros com sinal...)
© Gonçalo Tavares, Moisés Piedade
9
SEPS – REPRESENTAÇÃO EM VÍRGULA FIXA IV

Produto de dois nºs com n bit em formatos genéricos: Qm×Qk
n 
1 m
m

 

s
i
i

i
f
f

f
n
1 k
k


 

s
i
i

i
f
f

f
2
n 
2 m k
m 
k 1 n
n 1

 

s
i
f
f 
f


s
i
i
f

f
palavra de n bit que deve ser guardada em Qm  k 1-n



O formato resultante é Qm+k+1-n
Para guardar o resultado numa palavra de n bit neste formato é
necessário deslocar para a esquerda 1 bit (eliminando o bit de
sinal) e guardar a parte alta da palavra de 2n bit
Pode utilizar-se um formato mais preciso desde que o resultado
da multiplicação seja representável...
© Gonçalo Tavares, Moisés Piedade
10
SEPS – REPRESENTAÇÃO EM VÍRGULA FIXA V
Exemplos com palavras de n bit:
Qn-1×Qn-1 ï pode sempre guardar-se em Qn-1 porque |x ·y| ≤ 1


n1


n1


s
f
f

f
s
f
f

f
s
f
f




s
f
f
f

f
f
palavra de n bit que pode sempre ser guardada em Qn 1
Qn-2×Qn-2 ï pode sempre guardar-se em Qn-3 porque |x ·y| ≤ 4

n1


s
i
f

f
n1


s
i
f

f
s
f




s
i
i
f
f
f

f
f

f

f
palavra de n bit que pode sempre ser guardada em Qn 3
mas que se pode representar em Qn-2 se se verificar |x ·y| ≤ 2
n 1


s
i
f

f
passa a ser o bit de sinal!
n 1


s
i
f

f
s
n 1


i
f

f
f
f




i
i
f
palavra de n bit que pode ser guardada em Qn  2 se | x y| 2
ou em Qn-1 se |x ·y| ≤ 1
s
s
passam a ser bits de sinal!
n 1


s
i
f

f
s
s
i
i
f

f
f
f


palavra de n bit que pode ser guardada em Qn 1 se | x y|1
© Gonçalo Tavares, Moisés Piedade
11
SEPS – REPRESENTAÇÃO EM VÍRGULA
FLUTUANTE I

Standard IEEE 754: representação em vírgula flutuante com precisão
simples (32 bit):
31 30 29
23 22



s = bit de sinal (0 = positivo, 1 = negativo)

e = [e7 · · · e0] é o expoente (8 bit) que tem o valor decimal
1
0
7
e=
å ek 2k
0 £ e £ 255
k =0
O valor e=0 é reservado para representar o número zero. O valor e = 255 é
reservado para representar NaN e infinito

m=[m1 · · · m23] é a mantissa ou parte fraccionária (23 bit) e tem o valor decimal
23
m =
å mk 2-k
0 £ m £ 1 - 2-23
k =1
que corresponde à palavra binária 0.m1m2…m23
© Gonçalo Tavares, Moisés Piedade
12
SEPS – REPRESENTAÇÃO EM VÍRGULA
FLUTUANTE II

O valor numérico do número x é determinado pelas seguintes regras:
1. Se e = 255 e m ¹ 0 então x é NaN, independentemente de s
2. Se e = 255 e m = 0 então x = (-1)s ´ ¥
3. Se 0 < e < 255 então
s e -127
x = (-1) 2
(1 + m )
4. Se e = 0 então x = (-1)s´0
Exemplos:
Maior positivo: s = 0, e = 254, m = 1 - 2-23
x = (-1)0 2254-127 (1 + 1 - 2-23 )
= (-1)0 2254-127 (2 - 2-23 ) = 2128 - 2104 » 3.4 ´ 1038
Menor positivo: s = 0, e = 1, m = 0
x = (-1)0 21-127 (1 + 0)
= (-1)0 21-127 = 2-126 » 1.17 ´ 10-38
© Gonçalo Tavares, Moisés Piedade
13
SEPS – REPRESENTAÇÃO EM VÍRGULA
FLUTUANTE III

Características da representação em vírgula flutuante
float
double
long double
byte/bit
4/32
8/64
10/80
expoente
(bits)
8
11
15
mantissa
(bits)
23
52
64
precisão*
7
16
21
maior
positivo
» 2128 = 3.4 ´ 1038
» 21024 = 1.8 ´ 10308
» 216384 = 1.2 ´ 104932
menor
» 2-126 = 1.17 ´ 10-38 » 2-1022 = 2.2 ´ 10-308 » 2-16382 = 3.4 ´ 10-4932
positivo
*casas decimais (aproximadas) para se ter um erro absoluto relativo inferior a 10-3
© Gonçalo Tavares, Moisés Piedade
14