Teoremas de De Morgan

28/04/13
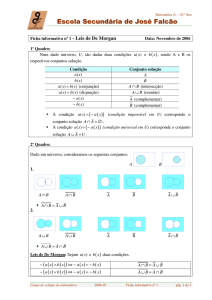
Teoremas de De Morgan – Wikipédia, a enciclopédia livre
Teoremas de De Morgan
Origem: Wikipédia, a enciclopédia livre.
Os teoremas do matemático De Morgan são propostas de simplificação de expressões em álgebra booleana de
grande contribuição. Definem regras usadas para converter operações lógicas OU em E e vice versa.
Sendo
e as operações em
sendo
e
assim definidas:
Operação lógica Símbolo Exemplos
Ou
+
E
Não
Índice
1 As leis
1.1 Lógica proposicional
1.2 Lógica booleana
1.3 Lógica booleana na eletrônica digital
1.4 Textual
1.5 Generalização
2 Prova
3 Referências
4 Ligações externas
As leis
Considere X e Y como variáveis booleanas ou proposições cuja resposta seja {Sim, Não} ou {Verdadeiro,
Falso} ou ainda {0,1}. Seguem as leis de De Morgan conforme algumas notações possíveis:
Lógica proposicional
1.
2.
pt.wikipedia.org/wiki/Teoremas_de_De_Morgan
1/4
28/04/13
Teoremas de De Morgan – Wikipédia, a enciclopédia livre
Lógica booleana
1.
2.
Lógica booleana na eletrônica digital
1.
2.
3. O complemento, ou negação de um produto (AND) de variáveis é igual a soma(OR) dos complementos
das variáveis.1
4. O complemento, ou negação de uma soma (OR) de variáveis é igual ao produto (AND) dos
complementos das variáveis.1
A figura 1.1 mostra o circuito que representa o 1. Teorema e a tabela abaixo representa sua respectiva tabela
verdade.
1.1 Teorema
X Y
0 0 1
1
0 1 1
1
1 0 1
1
1 1 0
0
A figura 1.2 mostra o circuito que representa o 1. Teorema e a tabela abaixo representa sua respectiva tabela
verdade.
X Y
0 0 1
1
0 1 0
0
1 0 0
0
1 1 0
0
Observada a equivalência na saída das tabelas, isto prova o mesmo comportamento lógico.
Considere a seguinte expressão:2
pt.wikipedia.org/wiki/Teoremas_de_De_Morgan
2/4
28/04/13
Teoremas de De Morgan – Wikipédia, a enciclopédia livre
1.2 Teorema
Aplicando os teoremas de De Morgan:
Textual
1. Não (X E Y) = Não (X) Ou Não (Y)
2. Não (X Ou Y) = Não (X) E Não (Y)
Generalização
A ideia é que ao "aplicar" a barra (operador Não) sobre uma outra operação, esta muda seu sinal, restando
uma barra para cada membro da operação. Exemplos:
Prova
Se de fato
então:
1.
2.
a)
primeiro usamos a propriedade distributiva do operador
depois a propriedade comutativo (passo não
mostrado), então vemos a soma de elementos complementares
b)
pt.wikipedia.org/wiki/Teoremas_de_De_Morgan
3/4
28/04/13
Teoremas de De Morgan – Wikipédia, a enciclopédia livre
Primeiro usamos a propriedade distributiva do operador depois usamos a propriedade de comutatividade
(esse passo não foi mostrado), então usamos a propriedade de elementos complementares
Os teoremas de DeMorgan são usados para provar que toda lógica booleana pode ser criada somente com
portas lógicas NAND ou NOR.
Referências
1. ↑ a b FLOYD, Thomas L.; Sistemas digitais: Fundamentos e aplicação, 9ª ed, página 250, Bookman, 2007,
Porto Alegre
2. ↑ TOCCI, Ronald; Sistemas digitais: princípios e aplicações, Ronald J. Tocci, Neal S. Widmer, Gregory L.
Moss, página 65, Pearson Education, São Paulo-SP, 2007.
Ligações externas
O Teorema de De Morgan
(http://www.eletronica24h.com.br/Curso%20Digital/aparte1/DeMorgan/demorgan.htm)
Obtida de "http://pt.wikipedia.org/w/index.php?title=Teoremas_de_De_Morgan&oldid=34802173"
Categorias: Teoremas de matemática Lógica Álgebra
Esta página foi modificada pela última vez à(s) 17h54min de 26 de março de 2013.
Este texto é disponibilizado nos termos da licença Atribuição-Partilha nos Mesmos Termos 3.0 não
Adaptada (CC BY-SA 3.0); pode estar sujeito a condições adicionais. Consulte as condições de uso
para mais detalhes.
pt.wikipedia.org/wiki/Teoremas_de_De_Morgan
4/4