Exercícios de Resistência dos Materiais A - Área 3

Exercícios de Resistência dos Materiais A - Área 3
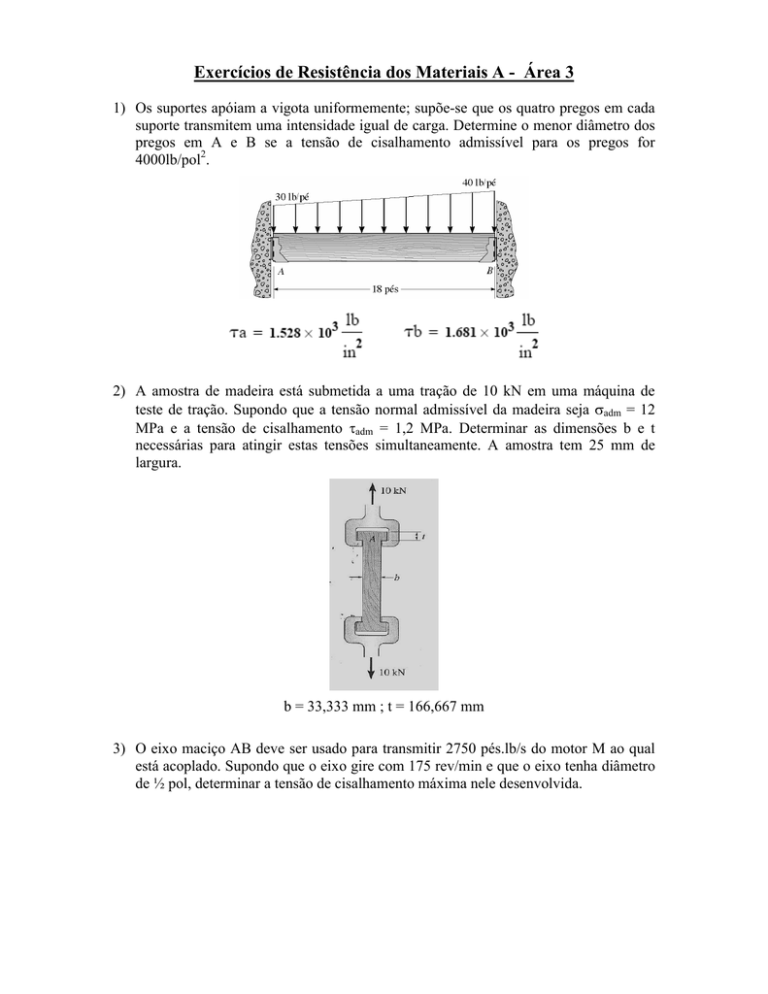
1) Os suportes apóiam a vigota uniformemente; supõe-se que os quatro pregos em cada
suporte transmitem uma intensidade igual de carga. Determine o menor diâmetro dos
pregos em A e B se a tensão de cisalhamento admissível para os pregos for
4000lb/pol2.
2) A amostra de madeira está submetida a uma tração de 10 kN em uma máquina de
teste de tração. Supondo que a tensão normal admissível da madeira seja σadm = 12
MPa e a tensão de cisalhamento τadm = 1,2 MPa. Determinar as dimensões b e t
necessárias para atingir estas tensões simultaneamente. A amostra tem 25 mm de
largura.
b = 33,333 mm ; t = 166,667 mm
3) O eixo maciço AB deve ser usado para transmitir 2750 pés.lb/s do motor M ao qual
está acoplado. Supondo que o eixo gire com 175 rev/min e que o eixo tenha diâmetro
de ½ pol, determinar a tensão de cisalhamento máxima nele desenvolvida.
Exercícios de Resistência dos Materiais A - Área 3
4) A peça de máquina de alumínio está sujeita a um momento M = 75 N.m. Determinar
a tensão de flexão criada nos pontos B e C da seção transversal. Desenhar a
distribuição de tensão que atua na seção transversal (bidimensional).
5) Um tubo de aço com diâmetro externo de 2,5 pol transmite 19000 pés.lb/s quando
gira a 2700 rev/min. Determinar o diâmetro interno d do tubo se a tensão de
cisalhamento admissível é 10000lbf/pol2.
di = 2,483 pol
Exercícios de Resistência dos Materiais A - Área 3
6) Determinar o peso máximo que pode ser aplicado na extremidade livre da viga
engastada mostrada na figura para que o coeficiente de segurança seja 1,2. Considerar
um material com tensão de escoamento igual a 60 kN/cm2
P = 0,67 kN
7) Supondo que o momento que atua sobre a seção transversal seja M=1000 lb.pé, a)
determinar a tensão de flexão máxima na viga? b) desenhar a distribuição de tensão
que atua na seção transversal? c) determinar a força resultante que as tensões de
flexão produzem na tabua superior A da viga?
;
8) Determinar a potência máxima (em CV) que pode ser transmitida por um eixo de 8
cm de diâmetro que gira a 360 rpm. Considerar tensão de escoamento igual a 2500
kgf/cm2 e coeficiente de segurança segundo a teoria de Guest igual a 3.
ou
Exercícios de Resistência dos Materiais A - Área 3
9) Uma viga simplesmente apoiada de três metros suporta uma carga distribuída de 425
kgf/m. Sua seção de altura total igual a 20cm tem uma inércia de 2145 cm4 e seu
centro de gravidade está a 13,5 cm da base. Apresentar um esquema mostrando a
descrição do problema. Apresentar o círculo de Mohr (esquema gráfico com os
valores) das tensões para y=2,5 cm e y=17,5 cm na seção mais solicitada.
;
10) Determinar a espessura t da seção se ela deve suportar um momento de flexão de
12,75 kN.m com um coeficiente de segurança de 2. Considerar tensão limite de tração
igual a 300 kgf/cm2, tensão limite de compressão igual a -750 kgf/cm2.
11) De acordo com a figura, a força P tende a fazer com que a peça superior (1) deslize
sobre a inferior (2). Sendo P = 4.000 Kgf, qual a tensão desenvolvida no plano de
contato entre as duas peças?
12) O aço de baixo teor de carbono usado em estruturas tem limite de resistência ao
cisalhamento de 31 kN/cm2 . Pede-se a força P necessária para se fazer um furo de 2.5
cm de diâmetro, em uma chapa deste aço com 3/8" de espessura.
Exercícios de Resistência dos Materiais A - Área 3
P = 231,9 kN
13) Considere-se o corpo de prova da figura, de seção transversal retangular 2.5 x 5
cm,usado para testar a resistência a tração da madeira. Sendo para a peroba de 1,3
kN/cm2 a tensão de ruptura ao cisalhamento, pede-se determinar comprimento
mínimo "a" indicado, para que a ruptura se de por tração e não por cisalhamento nos
encaixes do corpo de prova. Sabe-se que a carga de ruptura do corpo por tração é de
10,4 kN.
a> 0,8 cm
14) Determinar o diâmetro do pino D do dispositivo mecânico mostrado na figura,
utilizando a teoria de Guest com coeficiente de segurança igual a 3. O material do
pino é dúctil e apresenta tensão de escoamento igual a 3000 kgf/cm2 e coeficiente de
Poisson igual a 0,3.
Exercícios de Resistência dos Materiais A - Área 3
d = 1,83 cm
15) Considerando a figura onde a barra AB é torcida e a barra CD flexionada:
a) Determinar o valor da carga P que deve ser aplicada na estrutura para que o
coeficiente de segurança em relação à torção segundo a teoria de Guest seja 2?
b) Qual é o ângulo de torção θAB ?
c) Qual é, para esta carga, a máxima tensão de flexão? Em que ponto ela ocorre ?
d) Qual o coeficiente de segurança em relação à flexão?
Considerar tensão de escoamento igual a 4200 kgf/cm2 e a seção transversal mostrada.
O módulo de elasticidade transversal é 800000 kgf/cm2
;
;
;
;
16) A figura 1 mostra a união de uma chapa com outras duas mediante dois parafusos.
Para as forças atuantes:
Exercícios de Resistência dos Materiais A - Área 3
a) Determinar o diâmetro dos parafusos para garantir um coeficiente de segurança igual a
3. O material dos parafusos é dúctil e apresenta tensão de cisalhamento limite igual a 550
kgf/cm2.
b) Faça um círculo de Mohr mostrando as tensões principais para um diâmetro = 10 mm.
a) dp = 13,306mm ;
b)
17) Na figura 2 onde a barra AB é torcida sob a ação do momento Mt no ponto B, uma
linha longitudinal sofre uma distorção angular de 0,005 radiano. Se o módulo de
elasticidade transversal é 800000 kgf/cm2, determinar:
a) Os ângulos de torção unitário e total? (1,0 pt)
b) A tensão de torção máxima no ponto B? (0,5 pt)
c) O momento correspondente?
;
; Mt = 7,854*105 kgf.cm
;
18) Uma coluna de seção tubular com diâmetro externo de 3,50 mm e diâmetro interno
de 300mm e módulo de elasticidade de 200000N/mm2 está submetida a uma carga de
2000kN. Determine a rensão que atua na coluna assim como o seu encurtamento
sabendo que a coluna tem uma altura inicial de 5 m.
;
19) Os parafusos de 20 mm de diâmetro tem tensão de cisalhamento máxima de
220 MPa. Determine a força máxima que pode ser aplicada com um coeficiente de
segurança C.S. = 1,25 segundo a teoria de Guest
Exercícios de Resistência dos Materiais A - Área 3
F = 331,752 kN
20) A distância entre os pontos A e B é 3,00 m. Se os cabos 1 e 2 tem diâmetros de 15mm
e 18mm respectivamente, determine a posição de uma força F de 100 kN em relação
ao ponto A para os dois cabos terem a mesma tensão normal
Distância = 1,77 m
21) Uma viga de 6 m tem as condições de apoio e a seção transversal mostradas na figura.
Se a tensão de escoamento está limitada a 150 N/mm2, determine a carga distribuída
máxima admissível para está situação.
Exercícios de Resistência dos Materiais A - Área 3
22) A barra de seção circular da figura 3 tem 2,5 m de comprimento. Em 2 m tem
diâmetro de 200mm enquanto na outra parte tem diâmetro de 100 mm. Se a barra se
encontra engastada nas extremidades está submetida a um momento torçor de 50
kN.m no ponto B de muda de seção, calcule o ângulo de torção neste ponto.
Considerar G = 80000 N/mm2.
ângulo de torção = 0,37o
23) Considerando as informações da figura 3: a) determinar o coeficiente de segurança da
viga de seção I mostrada na figura, sabendo que o material é dúctil com tensão de
escoamento igual a 4000 kgf/cm2; b) Calcular as tensões para os pontos A e B
indicados na figura para a seção mais solicitada
S = 4,328;
;
24) A barra ABC está suportada por uma articulação em A e dois cabos BD e CE (ambos
de h m de comprimento, áreas das seções transversais iguais e de materiais de
módulos de elasticidade iguais), e está submetida a uma carga de 80 kN, como mostra
a figura. Desprezando a deformação por flexão e considerando a barra ABC como
sendo rígida, determinar as forças nos cabos e a reação na articulação A. Considerar
h= 1m.
Exercícios de Resistência dos Materiais A - Área 3
FBD = 24 kN ; FCE = 48 kN ; VA = 8 kN
25) Determinar o coeficiente de segurança do pino utilizado na rótula da estrutura
mostrada na figura, pela teoria de Saint Venant. Considerar tensão limite de tração
igual a 150 kgf/cm2, tensão limite de compressão igual a –250 kgf/cm2, coeficiente de
Poisson igual a 0,2 e diâmetro do pino igual a 2 cm. O pino trabalha com duas seções
resistentes
S = 2,12