Eletricidade - Meta Vestibulares

Física – ELETRICIDADE - UNICAMP - VESTIBULARES DE 2016-2010
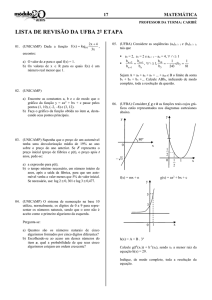
1. (Unicamp 2016) Muitos dispositivos de aquecimento usados em nosso cotidiano usam resistores elétricos como
fonte de calor. Um exemplo é o chuveiro elétrico, em que é possível escolher entre diferentes opções de potência
usadas no aquecimento da água, por exemplo, morno (M), quente (Q) e muito quente (MQ). Considere um
chuveiro que usa a associação de três resistores, iguais entre si, para oferecer essas três opções de temperatura. A
escolha é feita por uma chave que liga a rede elétrica entre o ponto indicado pela letra N e um outro ponto indicado
por M, Q ou MQ, de acordo com a opção de temperatura desejada. O esquema que representa corretamente o
circuito equivalente do chuveiro é
a)
b)
c)
d)
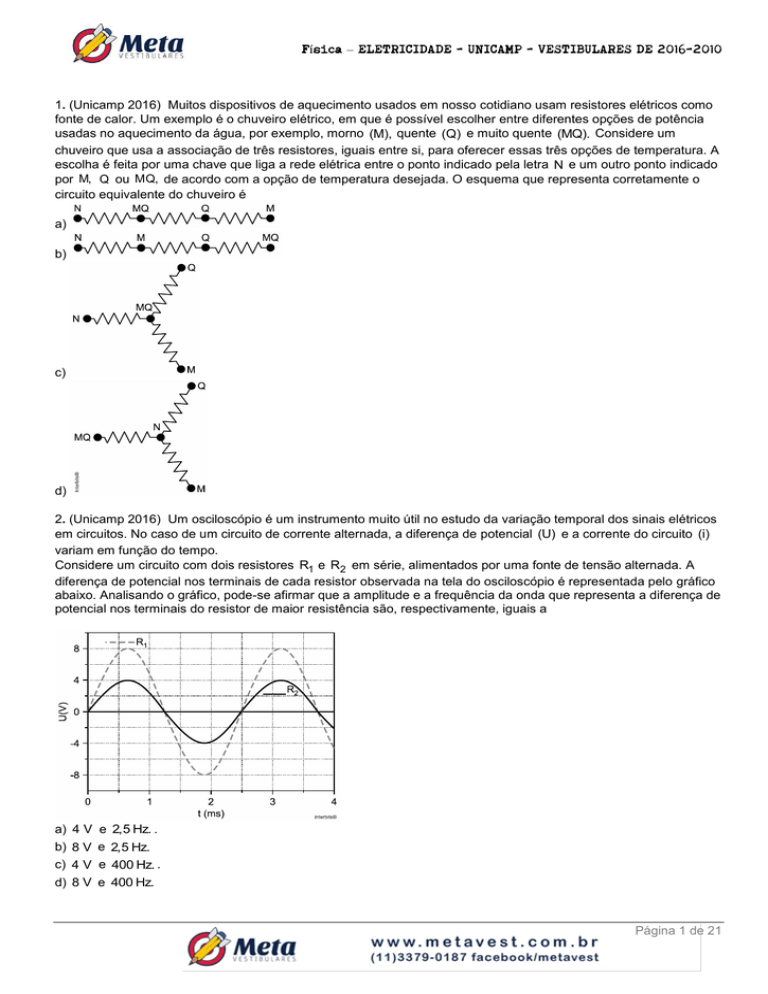
2. (Unicamp 2016) Um osciloscópio é um instrumento muito útil no estudo da variação temporal dos sinais elétricos
em circuitos. No caso de um circuito de corrente alternada, a diferença de potencial (U) e a corrente do circuito (i)
variam em função do tempo.
Considere um circuito com dois resistores R1 e R2 em série, alimentados por uma fonte de tensão alternada. A
diferença de potencial nos terminais de cada resistor observada na tela do osciloscópio é representada pelo gráfico
abaixo. Analisando o gráfico, pode-se afirmar que a amplitude e a frequência da onda que representa a diferença de
potencial nos terminais do resistor de maior resistência são, respectivamente, iguais a
a) 4 V e 2,5 Hz. .
b) 8 V e 2,5 Hz.
c) 4 V e 400 Hz. .
d) 8 V e 400 Hz.
Página 1 de 21
Física – ELETRICIDADE - UNICAMP - VESTIBULARES DE 2016-2010
3. (Unicamp 2015) Quando as fontes de tensão contínua que alimentam os aparelhos elétricos e eletrônicos são
desligadas, elas levam normalmente certo tempo para atingir a tensão de U  0 V. Um estudante interessado em
estudar tal fenômeno usa um amperímetro e um relógio para acompanhar o decréscimo da corrente que circula pelo
circuito a seguir em função do tempo, após a fonte ser desligada em t  0 s. Usando os valores de corrente e tempo
medidos pelo estudante, pode-se dizer que a diferença de potencial sobre o resistor R  0,5 kΩ para t  400 ms é
igual a
a) 6 V.
b) 12 V.
c) 20 V.
d) 40 V.
4. (Unicamp 2015) Por sua baixa eficiência energética, as lâmpadas incandescentes deixarão de ser
comercializadas para uso doméstico comum no Brasil. Nessas lâmpadas, apenas 5% da energia elétrica
consumida é convertida em luz visível, sendo o restante transformado em calor. Considerando uma lâmpada
incandescente que consome 60 W de potência elétrica, qual a energia perdida em forma de calor em uma hora de
operação?
a) 10.800 J.
b) 34.200 J.
c) 205.200 J.
d) 216.000 J.
Página 2 de 21
Física – ELETRICIDADE - UNICAMP - VESTIBULARES DE 2016-2010
5. (Unicamp 2015) A figura 1 apresentada a seguir representa a potência elétrica dissipada pelo filamento de
tungstênio de uma lâmpada incandescente em função da sua resistência elétrica. Já a figura 2 apresenta a
temperatura de operação do filamento em função de sua resistência elétrica. Se uma lâmpada em funcionamento
dissipa 150 W de potência elétrica, a temperatura do filamento da lâmpada é mais próxima de:
a) 325 C.
b) 1.250 C.
c) 3.000 C.
d) 3.750 C.
6. (Unicamp 2015) Um desafio tecnológico atual é a produção de baterias biocompatíveis e biodegradáveis que
possam ser usadas para alimentar dispositivos inteligentes com funções médicas. Um parâmetro importante de uma
bateria biocompatível é sua capacidade específica (C), definida como a sua carga por unidade massa, geralmente
dada em mAh / g. O gráfico abaixo mostra de maneira simplificada a diferença de potencial de uma bateria à base
de melanina em função de C.
a) Para uma diferença de potencial de 0,4V, que corrente média a bateria de massa m  5,0g fornece, supondo
que ela se descarregue completamente em um tempo t  4h?
b) Suponha que uma bateria preparada com C  10mAh / g esteja fornecendo uma corrente constante total i  2mA
a um dispositivo. Qual é a potência elétrica fornecida ao dispositivo nessa situação?
Página 3 de 21
Física – ELETRICIDADE - UNICAMP - VESTIBULARES DE 2016-2010
7. (Unicamp 2014) O sistema de imagens street view disponível na internet permite a visualização de vários lugares
do mundo através de fotografias de alta definição, tomadas em 360 graus, no nível da rua.
a) Em uma câmera fotográfica tradicional, como a representada na figura abaixo, a imagem é gravada em um filme
fotográfico para posterior revelação. A posição da lente é ajustada de modo a produzir a imagem no filme
colocado na parte posterior da câmera. Considere uma câmera para a qual um objeto muito distante fornece uma
imagem pontual no filme em uma posição p’ = 5 cm. O objeto é então colocado mais perto da câmera, em uma
posição p = 100 cm, e a distância entre a lente e o filme é ajustada até que uma imagem nítida real invertida se
forme no filme, conforme mostra a figura. Obtenha a variação da posição da imagem p’ decorrente da troca de
posição do objeto.
b) Nas câmeras fotográficas modernas, a captação da imagem é feita normalmente por um sensor tipo CCD
(Charge Couple Devide). Esse tipo de dispositivo possui trilhas de capacitores que acumulam cargas elétricas
proporcionalmente à intensidade da luz incidente em cada parte da trilha. Considere um conjunto de 3
capacitores de mesma capacitância C = 0,6 pF, ligados em série conforme a figura ao lado. Se o conjunto de
capacitores é submetido a uma diferença de potencial V = 5,0 V, qual é a carga elétrica total acumulada no
conjunto?
8. (Unicamp 2014) A atração e a repulsão entre partículas carregadas têm inúmeras aplicações industriais, tal
como a pintura eletrostática. As figuras abaixo mostram um mesmo conjunto de partículas carregadas, nos vértices
de um quadrado de lado a, que exercem forças eletrostáticas sobre a carga A no centro desse quadrado. Na
situação apresentada, o vetor que melhor representa a força resultante agindo sobre a carga A se encontra na
figura
a)
Página 4 de 21
Física – ELETRICIDADE - UNICAMP - VESTIBULARES DE 2016-2010
b)
c)
d)
9. (Unicamp 2014) No fenômeno de “Magneto impedância gigante”, a resistência elétrica de determinado material
pelo qual circula uma corrente alternada de frequência f varia com a aplicação de um campo magnético H . O
gráfico da figura 1 mostra a resistência elétrica de determinado fio de resistividade elétrica
ρ  64,8  108 Ωm em função da frequência f da corrente elétrica alternada que circula por esse fio, para diferentes
valores de H .
a) Como podemos ver na figura 1, o valor da resistência elétrica do fio para f  0 Hz é R  1,5Ω. Calcule o
comprimento L desse fio, cuja área de seção transversal vale A  1,296  108 m2.
b) Para altas frequências, a corrente elétrica alternada não está uniformemente distribuída na seção reta do fio, mas
sim confinada em uma região próxima a sua superfície. Esta região é determinada pelo comprimento de
ρ
, em que ρ é a resistividade do fio, f é a frequência da corrente elétrica
penetração, que é dado por δ  k
μr f
m Hz
. Sabendo que μr varia com o
Ω
campo magnético aplicado H , como mostra a figura 2, e que, para o particular valor de f  8 MHz temos
alternada, μr
é a permeabilidade magnética relativa do fio e k  500
R  4 Ω, calcule o valor de δ
para essa situação.
Página 5 de 21
Física – ELETRICIDADE - UNICAMP - VESTIBULARES DE 2016-2010
10. (Unicamp 2013) Em 2012 foi comemorado o centenário da descoberta dos raios cósmicos, que são partículas
provenientes do espaço.
a) Os neutrinos são partículas que atingem a Terra, provenientes em sua maioria do Sol. Sabendo-se que a
distância do Sol à Terra é igual a 1,5  1011 m , e considerando a velocidade dos neutrinos igual a 3,0  108 m/s ,
calcule o tempo de viagem de um neutrino solar até a Terra.
b) As partículas ionizam o ar e um instrumento usado para medir esta ionização é o eletroscópio. Ele consiste em
duas hastes metálicas que se repelem quando carregadas. De forma simplificada, as hastes podem ser tratadas
como dois pêndulos simples de mesma massa m e mesma carga q localizadas nas suas extremidades. O módulo
da força elétrica entre as cargas é dado por Fe  k
q2
d
2
, sendo k = 9  109 N m2/C2. Para a situação ilustrada na
figura abaixo, qual é a carga q, se m = 0,004 g?
11. (Unicamp 2013) O carro elétrico é uma alternativa aos veículos com motor a combustão interna. Qual é a
autonomia de um carro elétrico que se desloca a 60 km h, se a corrente elétrica empregada nesta velocidade é
igual a 50 A e a carga máxima armazenada em suas baterias é q  75 Ah?
a) 40,0 km.
b) 62,5 km.
c) 90,0 km.
d) 160,0 km.
12. (Unicamp 2013) Uma forma alternativa de transmissão de energia elétrica a grandes distâncias (das unidades
geradoras até os centros urbanos) consiste na utilização de linhas de transmissão de extensão aproximadamente
igual a meio comprimento de onda da corrente alternada transmitida. Este comprimento de onda é muito próximo do
comprimento de uma onda eletromagnética que viaja no ar com a mesma frequência da corrente alternada.
a) Qual é o comprimento de onda de uma onda eletromagnética que viaja no ar com uma frequência igual a 60 Hz?
A velocidade da luz no ar é c = 3  108 m/s.
b) Se a tensão na linha é de 500 kV e a potência transmitida é de 400 MW, qual é a corrente na linha?
13. (Unicamp 2012) Em 1963, Hodgkin e Huxley receberam o prêmio Nobel de Fisiologia por suas descobertas
sobre a geração de potenciais elétricos em neurônios. Membranas celulares separam o meio intracelular do meio
externo à célula, sendo polarizadas em decorrência do fluxo de íons. O acúmulo de cargas opostas nas superfícies
interna e externa faz com que a membrana possa ser tratada, de forma aproximada, como um capacitor.
a) Considere uma célula em que íons, de carga unitária e  1,6  10 19 C , cruzam a membrana e dão origem a uma
diferença de potencial elétrico de 80mV . Quantos íons atravessaram a membrana, cuja área é A  5  105 cm2 ,
se sua capacitância por unidade de área é Cárea  0,8  106 F/cm2 v?
b) Se uma membrana, inicialmente polarizada, é despolarizada por uma corrente de íons, qual a potência elétrica
entregue ao conjunto de íons no momento em que a diferença de potencial for 20mV e a corrente for
5  108 íons/s , sendo a carga de cada íon e  1,6  10 19 C ?
Página 6 de 21
Física – ELETRICIDADE - UNICAMP - VESTIBULARES DE 2016-2010
TEXTO PARA A PRÓXIMA QUESTÃO:
Atualmente há um número cada vez maior de equipamentos elétricos portáteis e isto tem levado a grandes esforços
no desenvolvimento de baterias com maior capacidade de carga, menor volume, menor peso, maior quantidade de
ciclos e menor tempo de recarga, entre outras qualidades.
14. (Unicamp 2012) Outro exemplo de desenvolvimento, com vistas a recargas rápidas, é o protótipo de uma
bateria de íon-lítio, com estrutura tridimensional. Considere que uma bateria, inicialmente descarregada, é
carregada com uma corrente média im  3,2 A até atingir sua carga máxima de Q = 0,8 Ah . O tempo gasto para
carregar a bateria é de
a) 240 minutos.
b) 90 minutos.
c) 15 minutos.
d) 4 minutos.
15. (Unicamp 2011) O grafeno é um material formado por uma única camada de átomos de carbono agrupados na
forma de hexágonos, como uma colmeia. Ele é um excelente condutor de eletricidade e de calor e é tão resistente
quanto o diamante. Os pesquisadores Geim e Novoselov receberam o premio Nobel de Física em 2010 por seus
estudos com o grafeno.
a) A quantidade de calor por unidade de tempo  que flui através de um material de área A e espessura d que
kA  T2  T1 
separa dois reservatórios com temperaturas distintas T1 e T2, e dada por  
, onde k é a
d
condutividade térmica do material. Considere que, em um experimento, uma folha de grafeno de A = 2,8  m2 e d
= 1,4 x 10−10 m separa dois microrreservatórios térmicos mantidos a temperaturas ligeiramente distintas T 1 = 300
K e T2 = 302 K. Usando o gráfico abaixo, que mostra a condutividade térmica k do grafeno em função da
temperatura, obtenha o fluxo de calor  que passa pela folha nessas condições.
b) A resistividade elétrica do grafeno à temperatura ambiente,   1,0  108 m , é menor que a dos melhores
condutores metálicos, como a prata e o cobre. Suponha que dois eletrodos são ligados por uma folha de grafeno
de comprimento L = 1, 4  m e área de secção transversal A = 70 nm 2, e que uma corrente i = 40  A percorra a
folha. Qual é a diferença de potencial entre os eletrodos?
16. (Unicamp 2011) Quando dois metais são colocados em contato formando uma junção, surge entre eles uma
diferença de potencial elétrico que depende da temperatura da junção.
a) Uma aplicação usual desse efeito é a medição de temperatura através da leitura da diferença de potencial da
junção. A vantagem desse tipo de termômetro, conhecido como termopar, é o seu baixo custo e a ampla faixa de
valores de temperatura que ele pode medir. O gráfico a) abaixo mostra a diferença de potencial U na junção em
função da temperatura para um termopar conhecido como Cromel-Alumel. Considere um balão fechado que
contém um gás ideal cuja temperatura é medida por um termopar Cromel-Alumel em contato térmico com o
balão. Inicialmente o termopar indica que a temperatura do gás no balão é Ti = 300 K. Se o balão tiver seu
Página 7 de 21
Física – ELETRICIDADE - UNICAMP - VESTIBULARES DE 2016-2010
volume quadruplicado e a pressão do gás for reduzida por um fator 3, qual será a variação ∆U = Ufinal − Uinicial da
diferença de potencial na junção do termopar?
b) Outra aplicação importante do mesmo efeito é o refrigerador Peltier. Neste caso, dois metais são montados como
mostra a figura b) abaixo. A corrente que flui pelo anel é responsável por transferir o calor de uma junção para a
outra. Considere que um Peltier é usado para refrigerar o circuito abaixo, e que este consegue drenar 10% da
potência total dissipada pelo circuito.
Dados R1 = 0,3  , R2 = 0, 4  e R3 = 1, 2  .
Qual é a corrente ic que circula no circuito, sabendo que o Peltier drena uma quantidade de calor Q = 540 J em ∆t
= 40 s?
TEXTO PARA AS PRÓXIMAS 2 QUESTÕES:
Quando um rolo de fita adesiva é desenrolado, ocorre uma transferência de cargas negativas da fita para o rolo,
conforme ilustrado na figura a seguir.
Quando o campo elétrico criado pela distribuição de cargas é maior que o campo elétrico de ruptura do meio, ocorre
uma descarga elétrica. Foi demonstrado recentemente que essa descarga pode ser utilizada como uma fonte
econômica de raios-X.
Página 8 de 21
Física – ELETRICIDADE - UNICAMP - VESTIBULARES DE 2016-2010
17. (Unicamp 2011) No ar, a ruptura dielétrica ocorre para campos elétricos a partir de E = 3,0 x 106 V/m . Suponha
que ocorra uma descarga elétrica entre a fita e o rolo para uma diferença de potencial V = 9 kV. Nessa situação,
pode-se afirmar que a distância máxima entre a fita e o rolo vale
a) 3 mm.
b) 27 mm.
c) 2 mm.
d) 37 nm.
18. (Unicamp 2011) Para um pedaço da fita de área A = 5,0×10−4 m2 mantido a uma distância constante d = 2,0
mm do rolo, a quantidade de cargas acumuladas é igual a Q = CV , sendo V a diferença de potencial entre a fita
C
A
. Nesse caso, a diferença de potencial entre a fita e o
desenrolada e o rolo e C  ε0
em que ε 0  9,0x10 12
Vm
d
rolo para Q = 4,5×10−9C é de
a) 1,2×102 V.
b) 5,0×10−4 V.
c) 2,0×103 V.
d) 1,0×10−20 V.
19. (Unicamp 2010) O Efeito Hall consiste no acúmulo de cargas dos lados de um fio condutor de corrente quando
esse fio está sujeito a um campo magnético perpendicular à corrente. Pode-se ver na figura (i) uma fita metálica
imersa num campo magnético B , perpendicular ao plano da fita, saindo do papel. Uma corrente elétrica atravessa a
fita, como resultado do movimento dos elétrons que têm velocidade v , de baixo para cima até entrar na região de
campo magnético. Na presença do campo magnético, os elétrons sofrem a ação da força magnética, FB ,
deslocando-se para um dos lados da fita. O acúmulo de cargas com sinais opostos nos lados da fita dá origem a um
campo elétrico no plano da fita, perpendicular à corrente. Esse campo produz uma força elétrica FE , contrária à
força magnética, e os elétrons param de ser desviados quando os módulos dessas forças se igualam, conforme
ilustra a figura (ii). Considere que o módulo do campo elétrico nessa situação é E = 1,0×10−4 V/m .
a) A fita tem largura L = 2,0 cm. Qual é a diferença de potencial medida pelo voltímetro V na situação da figura (ii)?
b) Os módulos da força magnética e da força elétrica da figura (ii) são dados pelas expressões FB = qvB e FE = qE ,
respectivamente, q sendo a carga elementar. Qual é a velocidade dos elétrons? O módulo do campo magnético é
B = 0,2 T.
20. (Unicamp 2010) A experimentação é parte essencial do método científico, e muitas vezes podemos fazer
medidas de grandezas físicas usando instrumentos extremamente simples.
a) Usando o relógio e a régua graduada em centímetros da figura a seguir, determine o módulo da velocidade que a
extremidade do ponteiro dos segundos (o mais fino) possui no seu movimento circular uniforme.
Página 9 de 21
Física – ELETRICIDADE - UNICAMP - VESTIBULARES DE 2016-2010
b) Para o seu funcionamento, o relógio usa uma pilha que, quando nova, tem a capacidade de fornecer uma carga
q = 2,4 Ah = 8,64×103 C. Observa-se que o relógio funciona durante 400 dias até que a pilha fique completamente
descarregada. Qual é a corrente elétrica média fornecida pela pilha?
21. (Unicamp 2010) Telas de visualização sensíveis ao toque são muito práticas e cada vez mais utilizadas em
aparelhos celulares, computadores e caixas eletrônicos. Uma tecnologia frequentemente usada é a das telas
resistivas, em que duas camadas condutoras transparentes são separadas por pontos isolantes que impedem o
contato elétrico.
a) O contato elétrico entre as camadas é estabelecido quando o dedo exerce uma força F sobre a tela, conforme
mostra a figura a seguir. A área de contato da ponta de um dedo é igual a A = 0,25 cm2. Baseado na sua
experiência cotidiana, estime o módulo da força exercida por um dedo em uma tela ou teclado convencional, e
em seguida calcule a pressão exercida pelo dedo. Caso julgue necessário, use o peso de objetos conhecidos
como guia para a sua estimativa.
b) O circuito simplificado da figura no espaço de resposta ilustra como é feita a detecção da posição do toque em
telas resistivas. Uma bateria fornece uma diferença de potencial U = 6 V ao circuito de resistores idênticos de R =
2 kÙ. Se o contato elétrico for estabelecido apenas na posição representada pela chave A, calcule a diferença de
potencial entre C e D do circuito.
Página 10 de 21
Física – ELETRICIDADE - UNICAMP - VESTIBULARES DE 2016-2010
22. (Unicamp 2010) Ruídos sonoros podem ser motivo de conflito entre diferentes gerações no ambiente familiar.
a) Uma onda sonora só pode ser detectada pelo ouvido humano quando ela tem uma intensidade igual ou superior
a um limite I0, denominado limiar de intensidade sonora audível. O limiar I0 depende da frequência da onda e
varia com o sexo e com a idade. Nos gráficos no espaço de resposta, mostra-se a variação desse limiar homens,
I0H, e para mulheres, I0M, em diversas idades, em função da frequência da onda.
Considerando uma onda sonora de frequência f = 6 kHz, obtenha as respectivas idades de homens e mulheres
para as quais os limiares de intensidade sonora, em ambos os casos, valem I0H = I0M =10-11 W/m2.
b) A perda da audição decorrente do avanço da idade leva à utilização de aparelhos auditivos, cuja finalidade é
amplificar sinais sonoros na faixa específica de frequência da deficiência auditiva, facilitando o convívio do idoso
com os demais membros da família. Um esquema simplificado de um aparelho amplificador é representado a
seguir.
Considere que uma onda sonora provoque uma diferença de potencial no circuito de entrada do aparelho
amplificador igual a Ve = 10 mV e que a diferença de potencial de saída Vs é igual a 50 vezes a de entrada Ve.
Sabendo que a potência elétrica no circuito de saída é Ps = 0,3 mW calcule a corrente elétrica is no circuito de saída.
Página 11 de 21
Física – ELETRICIDADE - UNICAMP - VESTIBULARES DE 2016-2010
Gabarito:
Resposta da questão 1:
[A]
Como a diferença de potencial (U) é a mesma nos três casos, a potência pode ser calculada pela expressão:
P
U2
.
R
Assim, a conexão de menor resistência equivalente é a que dissipa a maior potência:
Como:
PMQ  PQ  PM  RMQ  RQ  RM.
A figura ilustra essas conexões:
Resposta da questão 2:
[D]
Resistores em série são percorridos pela mesma corrente elétrica. Como U  R i, o resistor de maior resistência
está sob maior tensão. Analisando o gráfico, observamos que num ponto de pico, a ddp em R1 é 8 V e em R2 é
4 V. Logo, R1 é o resistor de maior resistência. Assim, do gráfico:
 A8V


1
1
3
 0,4  103 
 T  2,5 ms  2,5  10 s  f  
T 2,5  103

f  400 Hz.
Resposta da questão 3:
[A]
Dado: R  0,5 kΩ  0,5  103 Ω; i  12 mA  12  103 A.
Aplicando a 1ª Lei de Ohm:
U  R i  0,5  103  12  103 
U  6 V.
Resposta da questão 4:
[C]
Eperd  95% Econs  0,95 Pcons Δt  Eperd  0,95  60  3.600 
Eperd  205.200 J.
Resposta da questão 5:
[C]
Basta seguir a seta em cada um dos gráficos.
Página 12 de 21
Física – ELETRICIDADE - UNICAMP - VESTIBULARES DE 2016-2010
No gráfico da figura 1, para a potência de 150 W obtemos que a resistência é de 325Ω. No gráfico da figura 2, para
a resistência de 325Ω, obtemos a temperatura de 3.000C.
Resposta da questão 6:
A figura ilustra os pontos destacados no gráfico que são relevantes para as resoluções dos dois itens.
a) Dados: V  0,4 V; m  5 g; Δt  4 h.
Do gráfico:
Página 13 de 21
Física – ELETRICIDADE - UNICAMP - VESTIBULARES DE 2016-2010
V  0,4 V  C  20 mAh/g.
Q  m C  5  20  Q  100 mAh.
im 
Q 100


Δt
4
Q  25 mA.
b) Dados: i  2 mA.
Do gráfico:
C  10 mAh/g  V  0,2 V .
P  i V  2  0,2 
P  0,4 mW.
Resposta da questão 7:
a) Sendo a lente convergente e o objeto muito distante (impróprio), a imagem forma-se no foco imagem. Assim:
f  p'  5 cm.
Para a nova situação, a imagem é p’’. Aplicando a equação dos pontos conjugados:
1 1 1
1
1
1
1 20  1 19
100
 






 p'' 
cm.
f p p''
5 100 p''
p''
100
100
19
A variação na posição da imagem é:
p''  p' 
100
100  95
5 
19
19

p''  p' 
5
cm.
19
b) Dados: n = 3; C = 0,6 pF; V = 5 V.
Para uma associação de n capacitores de mesma capacitância C, a capacitância equivalente é:
C 0,6
Ceq  
 Ceq  0,2 pF.
n
3
Calculando a carga armazenada:
Q  Ceq V  0,2  5 

Q  1 pC  1 10 12 C.
Resposta da questão 8:
[D]
A figura mostra as forças atrativas e repulsivas agindo sobre a carga A, bem como a resultante dessas forças.
Resposta da questão 9:
a) Dados: R  1,5Ω; ρ  64,8  108 Ω  m; A  1,296  108 m2.
Da segunda lei de Ohm:
Página 14 de 21
Física – ELETRICIDADE - UNICAMP - VESTIBULARES DE 2016-2010
R
ρL
A
 L
R A 1,5  1,296  10 8

 1,5  0,02  0,03 m 
ρ
64,8  108
L  3 cm.
b) Do gráfico da Figura 1, conforme ponto assinalado:
f = 8 MHz e R  4Ω  H  35Oe.
Do gráfico da Figura 2, conforme ponto assinalado:
H  35Oe  μr  1.000
Substituindo os valores obtidos na expressão fornecida:
δk
64,8  10 8
ρ
 δ  500
 500 81 10 18  500  9  10 9  δ  4,5  10 6 m 
μr f
103  8  106
δ  4,5 μm.
Resposta da questão 10:
ΔS
a) Como V 
, teremos:
Δt
V
ΔS
1,5x1011
 3,0x108 
 Δt  0,5x103 s
Δt
Δt
Resposta: Δt  5,0x102 s
b) T  mg  Fe  0
Página 15 de 21
Física – ELETRICIDADE - UNICAMP - VESTIBULARES DE 2016-2010
Tg45 
Fe
F
 1  e  Fe  mg
mg
mg
Como Fe  k
Fe  mg  k
q2
d2
:
q2
 mg
d2
De acordo com o enunciado:
k = 9  109 N m2/C2
d = 3 cm = 3x10-2 m
m = 0,004 g = 4x10-6 kg
g = 10 m/s2
Substituindo os valores:
k
q2
d2
 mg 
9x109.q2
(3x102 )2
 4x106.10  q2  4x1018
Resposta: | q | 2,0x109 C
Resposta da questão 11:
[C]
A quantidade de carga elétrica contida na bateria é dada por:
q  i  Δt
75Ah  50A  Δt
75
h
50
Δt  1,5h
Δt 
Sabendo que a autonomia (em horas) da bateria é 1,5 horas temos:
Δs  v  Δt
Δs  60  1,5
Δs  90 km
Resposta da questão 12:
a) Dados: c = 3  108 m/s; f = 60 Hz.
Da equação fundamental da ondulatória:
c 3  108

 λ  5  106 m.
f
60
b) Dados: P = 400 MW = 400  106 W; U = 500 kV = 500  103 V.
Da expressão da potência elétrica:
cλ f  λ
Página 16 de 21
Física – ELETRICIDADE - UNICAMP - VESTIBULARES DE 2016-2010
PU i  i
P 400  106

U 500  103
 i  800 A.
Resposta da questão 13:
a) Dados: e  1,6  1019 C; A  5  105 cm2; U  80 mV  8  102 V; Cárea  0,8  106F / cm2.
A capacitância da membrana é o produto da capacitância por unidade de área pela área da membrana.
 F 
  5  10 5 cm2
C  Cárea A  0,8  10 6 
 C  4  10 11 F.
 cm2 




Q
C 
U

Q  ne

 C
ne
U
 n

C U 4  1011  8  102

e
1,6  1019

n  2,0  107 íons.
b) Dados: e  1,6  1019 C; z  5  108 íons / s; U  20 mV  2  102 V.
 íons 
19  C 
P  Ui  P  U z e  2  10 2  V   5  108 
 1,6  10


 s 
 íon 

P  1,6  10 12 W.
Resposta da questão 14:
[C]
Da definição de corrente elétrica:
Q
Q 0,8 Ah
im 
 t  
 0,25 h  0,25  60 min  
t
im
3,2 A
t  15 min.
Resposta da questão 15:
Obs: o examinador poderia ter sido mais ameno e facilitado um pouco a resolução, dando a dica de que 1 m2 =
10–12 m2. Por isso, a questão foi considerada de dificuldade elevada. Muitos candidatos podem não ter percebido o
detalhe da transformação.
a) Dados: A = 2,8 m2 = 2,8  (10–6 m)2 = 2,8  10–12 m2; d = 1,4  10–10 m; T1 = 300 K; T2 = 302 K.
Como o intervalo de temperatura em questão é pequeno, podemos considerar a condutividade térmica constante.
Do gráfico:
k = 4  103 W/(mK).
Substituindo esses valores na expressão dada:
kA  T2  T1 
4  103  2,8  1012  302  300 


d
1,4  1010

  1,6  102 W .
b) Dados:  = 1,0  10–8 m; L = 1,4 m = 1,4  10–6 m; A = 70 nm2 = 70  (10–9 m)2 = 70  10–18 m2; i = 40 A = 40 
10–6 A.
Da 1ª lei de Ohm: U  R i 
L
1 10 8  1,4  10 6  40  10 6


LU i
A
70  10 18
Da 2ª lei de Ohm: R   
A
U = 8,0  10–3 V.
Página 17 de 21
Física – ELETRICIDADE - UNICAMP - VESTIBULARES DE 2016-2010
Resposta da questão 16:
a) Dados: Ti = 300 K; Pf =
Pi
3
; Vf = 4 Vi.
Aplicando a equação geral dos gases ideais:
Pi
4Vi
Pi Vi Pf Vf
Pi Vi
4


 3
 Tf  300
Ti
Tf
300
Tf
3
Tf = 400 K.
Tinicial  300 K  Uinicial  12 mV
Do gráfico dado: 
Tfinal  400 K  Ufinal  16 mV
U = 4 mV.

 U  Ufinal  Uinicial  16  12 
b) Dados: R1 = 0,3  , R2 = 0, 4  ; R3 = 1, 2  ; Q = 540 J; t = 40 s.
Calculando a resistência equivalente do circuito mostrado:
R  R3
0,4  1,2
R eq  R1  2
 0,3 
 0,3  0,3  R eq  0,6 .
R2  R3
0,4  1,2
A potência drenada é:
Q 540
Pdren 

 Pdren  13,5 W.
t
40
Mas a potência drenada é 10% da potência total dissipada:
P
13,5
 PT  135 W.
Pdren = 0,1 PT  PT  dren 
0,1
0,1
Usando a expressão da potência dissipada em um circuito:
PT
135
PT  Req ic2  ic 

 225 
Req
0,6
Ic = 15 A.
Resposta da questão 17:
[A]
Dados: E = 3  106 V/m; V = 9 kV = 9  103 V.
Como esse campo elétrico pode ser considerado uniforme, podemos escrever:
Ed = V  d 
V 9  103
= 3  10–3 m  d = 3 mm.

E 3  106
Resposta da questão 18:
[C]
Dados: A = 5,0  10–4 m2; d = 2 mm = 2  10–3; 0  9  10–12
C
; Q = 4,5  10–9 C.
V m
Combinando as expressões dadas:
A

(I)
Q d
C  ε0
 A
 (I) em II  Q   ε0  V  V 
.
d

d
ε


0 A
Q  C V (II)

Substituindo valores:
4,5  109  2  103
 V = 2,0  103 V.
V
9  1012  5  104
Página 18 de 21
Física – ELETRICIDADE - UNICAMP - VESTIBULARES DE 2016-2010
Resposta da questão 19:
a) Dados: E  1,0  104 V m; L  2,0 cm  2,0  102 m.
Sendo U a ddp indicada pelo voltímetro V, temos:
U  E L  10 –4  2  10 –2  U  2  10 –6 V 
U  2V.
b) No equilíbrio:
FE  FB  qE  qvB  v 
E 1,0  10 4


B
0,2
v  5  10 4 m s.
Resposta da questão 20:
a) Dado:  = 3.
Vejamos as medidas assinaladas na figura a seguir.
Nessa figura, obtemos para o diâmetro do ponteiro dos segundos: D = 58,0 mm.
O período desse ponteiro é: T = 60 s.
A cada volta, o espaço percorrido pela extremidade desse ponteiro é: S =  D.
v=
S  D 3 (58)
174
 v=



60
t
T
60
v = 2,9 mm/s.
Uma segunda solução é considerarmos que, entre as marcas de 14 s e 16 s, a trajetória da extremidade do ponteiro
é praticamente retilínea, aproximadamente, igual a 6,0 mm, como destacado na figura.
v=
S 6,0
 v = 3,0 mm/s.

t
2
Página 19 de 21
Física – ELETRICIDADE - UNICAMP - VESTIBULARES DE 2016-2010
b) Dados: q = 2,4 A.h = 8,64  103 C; t = 400 dias = (400  24) h.
A corrente elétrica média é dada por:
q
2,4
0,1


 2,5  104 A 
t 400  24 400
i = 0,25 mA.
i=
Resposta da questão 21:
a) Dado: A = 0,25 cm 2 = 0,25  10–4 m2.
A intensidade da força exercida pelo dedo é, baseada na experiência do cotidiano, equivalente ao peso de um corpo
de massa 100 g = 0,1 kg. Assim:
F = P = m g = 0,1(10) = 1 N.
A pressão é:
p=
F
1
 p = 4  104 N/m2.

A 0,25  104
b) Dados: R = 2 k; U = 6 V.
Fechando a chave A, o percurso da corrente elétrica é o indicado na figura a seguir.
A resistência equivalente é:
3 R 3 (2)
R
 Req = 3 k = 3  103 .
R 

2
2
3
A corrente no circuito é, então:
Req =
U = Req I  I 
U
6
 I = 2  10–3 A..

Req 3  103
A corrente I divide-se igualmente para os dois ramos em paralelo, uma vez que eles têm resistências iguais. Assim:
I 2  10 3
=
 i = 1  10–3 A
2
2
Calculando a diferença de potencial entre os pontos C e D:
i=
UCD = R i = (2  103)  (1  10–3) 
UCD = 2 V.
Página 20 de 21
Física – ELETRICIDADE - UNICAMP - VESTIBULARES DE 2016-2010
Resposta da questão 22:
a)
De acordo com os pontos assinalados nos gráficos, a resposta é: 35 anos para homens e 45 anos para as
mulheres.
b) a potência elétrica é dada por: Ps = Vsis e Vs=50Vc . Assim, is 
0,3mW
 0,6 mA
50x10mV
Página 21 de 21