PROFESSOR DA TURMA: CARIBÉ LISTA DE REVISÃO DA UFBA 2

17
MATEMÁTICA
PROFESSOR DA TURMA: CARIBÉ
LISTA DE REVISÃO DA UFBA 2a ETAPA
01. (UNICAMP) Dada a função f ( x )  log10
2x  4
,
3x
encontre:
a) O valor de x para o qual f(x) = 1.
b) Os valores de x  R para os quais f(x) é um
número real menor que 1.
05. (UFBA) Considere as seqüências (an)n
tais que
 1
e (bn)n
 1,
 a1 = 2, a1 = 2 e an + 1 – an = 4,    1
bn  2 b n 1
b
1
1


,   1, 10  
e b5 
bn 1
bn
b5
243
81
Sejam A = a5 + a6 + a7 + ... + a20 e B o limite da soma
b1 + b2 + b3 +... Calcule ABb3, indicando de modo
completo, toda a resolução da questão.
02. (UNICAMP)
a) Encontre as constantes a, b e c de modo que o
gráfico da função y = ax2 + bx + c passe pelos
pontos (1, 10), (–2, –8) e (3, 12).
b) Faça o gráfico da função obtida no item a, destacando seus pontos principais.
03. (UNICAMP) Suponha que o preço de um automóvel
tenha uma desvalorização média de 19% ao ano
sobre o preço do ano anterior. Se F representa o
preço inicial (preço de fábrica e p(t), o preço após t
anos, pede-se:
a) a expressão para p(t);
b) o tempo mínimo necessário, em número inteiro de
anos, após a saída da fábrica, para que um automóvel venha a valer menos que 5% do valor inicial.
Se necessário, use: log 2  0, 301 e log 3  0,477.
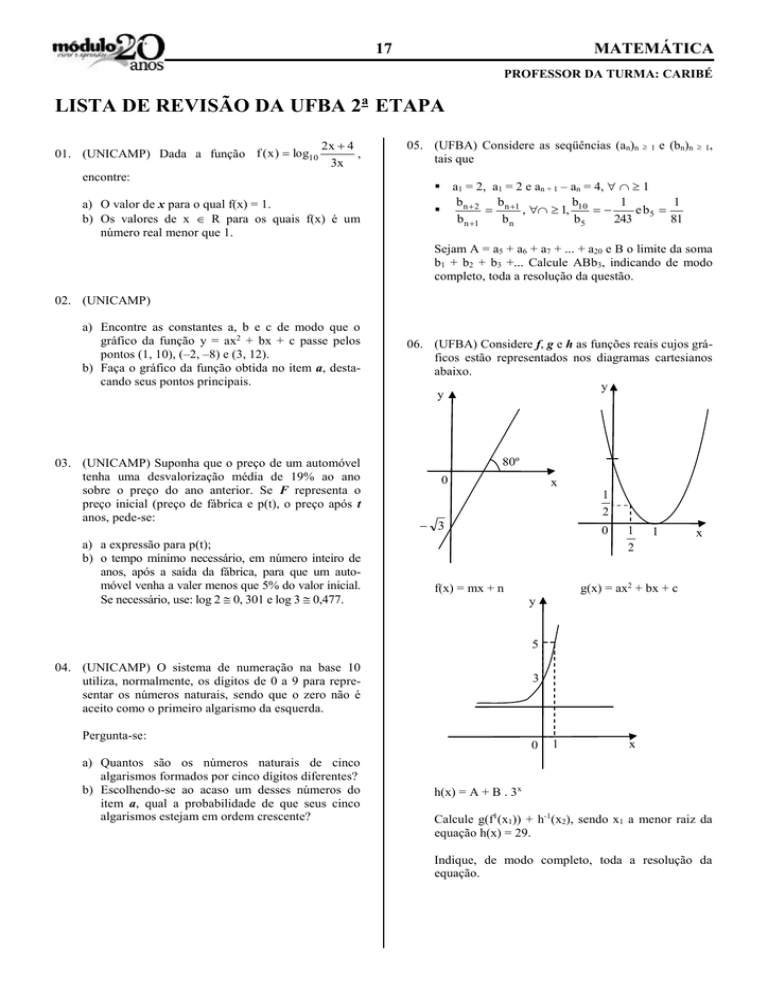
06. (UFBA) Considere f, g e h as funções reais cujos gráficos estão representados nos diagramas cartesianos
abaixo.
y
y
80º
0
x
1
2
 3
0
1
2
1
x
g(x) = ax2 + bx + c
f(x) = mx + n
y
5
04. (UNICAMP) O sistema de numeração na base 10
utiliza, normalmente, os dígitos de 0 a 9 para representar os números naturais, sendo que o zero não é
aceito como o primeiro algarismo da esquerda.
3
Pergunta-se:
a) Quantos são os números naturais de cinco
algarismos formados por cinco dígitos diferentes?
b) Escolhendo-se ao acaso um desses números do
item a, qual a probabilidade de que seus cinco
algarismos estejam em ordem crescente?
0
1
x
h(x) = A + B . 3x
Calcule g(f1(x1)) + h-1(x2), sendo x1 a menor raiz da
equação h(x) = 29.
Indique, de modo completo, toda a resolução da
equação.