Recursividade à Esquerda

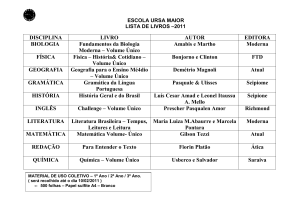
Compiladores
Prof. Bruno Moreno
Aula 9 – 06/05/2011
Como transformar uma
expressão regular em um
AFN?
Exp. Regular para AFN

Para E
Para a

Para s | t

Exp. Regular para AFN

Para st

Para s*
Exemplo

R = (a|b)*abb
st
s*
s|t
SAÍDA DO ANALISADOR
LÉXICO
Saída do Analisador Léxico

Fornece dois elementos para cada símbolo

Símbolo propriamente dito (posição na memória)


Ou apontando para ele
Um número que identifica a classe do símbolo
Saída do Analisador Léxico

Tabela de Símbolos (exemplo)
begin
SÍMBOLO
ID_CLASSE
Indefinido
0
Identificador
1
Inteiro
2
Begin
ab + (x2*y)/35 /* expressão aritmética */
end
CHAMADA
SAÍDA
SIGNIFICADO
3
1ª
3, “begin”
begin
Abs
4
2ª
1, “ab”
ab
End
5
3ª
8, “+”
+
(
6
4ª
6, “(“
(
)
7
5ª
1, “x2”
x2
+
8
6ª
10, “*”
*
-
9
7ª
1, “y”
y
*
10
8ª
7, “)”
)
/
11
9ª
11, “/”
/
**
12
10
2, “35”
35
:=
13
11ª
5, “end”
end
O ANALISADOR SINTÁTICO
O Analisador Sintático

O analisador sintático obtém uma cadeia de
tokens proveniente do analisador léxico
O Analisador Sintático

Verifica se esta cadeia pode ser gerada pela
gramática da linguagem-fonte
O Analisador Sintático

Relata erros de sintaxe
Recupera-se do erro para que a compilação
continue

Função do analisador sintático



Verificar se as construções usadas no programa
estão gramaticalmente corretas
Em uma linguagem natural é semelhante a
avaliar a construção frasal que obriga ter, por
exemplo, sujeito, verbo e predicado
Analisador Sintático

Já estudamos previamente os principal
artefatos de investigação utilizados pelo
Analisador Sintático
Árvores de decisão e Gramáticas
Analisador Sintático

Existem duas formas de realizar a análise
sintática

Análise descendente (top-down)


Análise ascendente (bottom-up)


Constroem as árvores de cima para baixo (raiz para folhas)
Constroem as árvores de baixo para cima (folhas para raiz)
Em ambos os casos, a entrada é varrida da
esquerda para a direita, um símbolo de cada vez
Analisador Sintático

Normalmente, as estruturas sintáticas válidas
são especificadas através de uma gramática
livre de contexto



Descreve as regras de formação de sentenças da
linguagem
A gramática é formada por regras de produções
Cada produção é uma regra de formação,
mostrando como um símbolo pode gerar (ou
produzir) outros
Gramática Livre de Contexto

Produções na forma


Por que “Livre de Contexto”?


A→a
Não terminal A pode ser substituído por a em
qualquer contexto, sem depender de qualquer
análise dos símbolos que sucedem ou
antecedem A
Diferente das gramáticas sensíveis ao
contexto

a → b, com a ∈ (N U T)+ e b ∈ (N U T)*
Gramática Livre de Contexto

Qualquer gramática G = {N, T, P, S}




N – Conjunto de símbolos não terminais
T – Conjunto de símbolos terminais
P – Conjunto de regras
S – Símbolo inicial
Gramática Livre de Contexto

Exemplo



G = ({E}, {+, -, *, /, ), (, x}, P, E}
P = E → E + E | E – E | E * E | E / E | (E)
Sentença: x+x*x
E
E
+
E
x
E
*
x
E
x
|x
Gramática Livre de Contexto

Exemplo



G = ({<num>, <digit>}, {0, 1, ..., 9}, P, <num>)
P = <num> → <num><digit> | <digit>
<digit> → 0, 1, ..., 9
Sentença: 45
<num>
<num>
<digit>
<digit>
5
4
Derivação mais à esquerda


É a seqüência de formas sentenciais que se
obtém derivando sempre o símbolo nãoterminal mais à esquerda
Exemplo



G = ({E}, {+, -, *, /, ), (, x}, P, E}
P = E → E + E | E – E | E * E | E / E | (E)
Sentença: x+x*x

E→E+E→ x+E→x+E*E→x+x*E →x+x*x
|x
Derivação mais à direita


É a sequencia de formas sentenciais que se
obtém derivando sempre o símbolo nãoterminal mais à direita
Exemplo



G = ({E}, {+, -, *, /, ), (, x}, P, E}
P = E → E + E | E – E | E * E | E / E | (E)
|x
Sentença: x+x*x

E→E+E→ E+E*E→E+E*x →E+x*x→x+x*x
Gramática Ambígua


É a gramática que permite construir mais de uma árvore
de derivação para uma mesma sentença
Exemplo


G = ({E}, {+, -, *, /, ), (, x}, P, E}
P = E → E + E | E – E | E * E | E / E | (E)
E
E
E
x
+
*
E
x
|x
E
E
E
+
E
x
x
E
*
x
E
x
Gramáticas Ambíguas

Qual o problema de uma gramática
ambígua?


Reconhecedores de linguagens exigem
derivações unívocas para obter um bom
desempenho
E também para concluir a derivação sintática
Gramáticas Ambíguas

Qual o problema lógico, de interpretação, nas
duas árvores de derivação a seguir?
E
E
E
x
+
*
E
E
E
E
+
E
x
x
E
*
x
+ é executado em primeiro lugar
x
E
x
* é executado em primeiro lugar
Gramáticas Ambíguas

Resolução de ambiguidade


Não existe um procedimento geral para retirar
ambigüidade de uma linguagem
Além disso, existem gramáticas em que é
impossível eliminar produções ambíguas

Linguagens Inerentemente Ambíguas
LINGUAGENS
INERENTEMENTE AMBÍGUAS
Linguagens Inerentemente
Ambíguas


São aquelas que qualquer GLC que a
descreva é ambígua
Exemplo

{ w | w = anbncmdm | anbmcmdn, n ≥ 1, m ≤ 1}


Para n =1, m = 2
w = abc2d2 ou ab2c2d
RECURSIVIDADE
Gramática recursiva à
esquerda

Permite a derivação




A → Aa para algum A ∈ N
Um não terminal (A) deriva ele mesmo, de forma
direta ou indireta, como símbolo mais à
esquerda
Reconhecedores top-down exigem que a
gramática não seja recursiva à esquerda
Quando a recursão é direta, a eliminação é
simples
Gramática recursiva à
esquerda


Quando a recursão é indireta, a eliminação
requer que a gramática seja inicialmente
simplificada
Gramática simplificada

É uma GLC que não apresenta símbolos inúteis
TRANSFORMAÇÃO DE GLCS
Transformação de GLCs


O processo de transformação de uma GLC
se caracteriza por transformar uma gramática
sem que ela perca a qualidade de gerar a
mesma linguagem
Gramáticas que geram mesma linguagem
utilizando regras de produção diferentes são
chamadas de gramáticas equivalentes
ELIMINAÇÃO DE RECURSIVIDADE
À ESQUERDA
Eliminação de Recursividade à
Esquerda

Para recursividade direta


Pode ser eliminada manualmente
Para recursividade indireta

Primeiramente, a gramática deve ser simplificada
Recursividade à Esquerda

Eliminação da recursividade direta
Substituir cada regra da forma
A → Aa1 | Aa2 | ... | Aan| b1 | b2 | ... | bm
onde nenhum bi começa por A, por
A → b1X | b2X | ... | bmX
X → a1X | a2X | ... | anX | E
Se produções vazias não são permitidas, a
substituição deve ser:
A → b1 | b2 | ... | bm | b1X | b2X | ... | bmX
X → a1 | a2 | ... | an | a1X | a2X | ... | anX
Recursividade à Esquerda
(Exemplo 1)


Linguagem: b(a)*
Com recursividade

A → Aa | b
b, ba, baa, baaa, ...
1º Passo: Identificar recursão
Recursividade à Esquerda
(Exemplo 1)


Linguagem: b(a)*
Com recursividade

A → Aa | b

A → bA’
b, ba, baa, baaa, ...
1º Passo: Identificar recursão
2º Passo: Para cada produção com
recursão
2.1: O não terminal que gera a regra de
produção deve receber agora a parte não
recursiva concatenada com um novo não
terminal
A → bA’
Recursividade à Esquerda
(Exemplo 1)


Linguagem: b(a)*
Com recursividade

A → Aa | b

A → bA’
A’ → aA’ | E

b, ba, baa, baaa, ...
1º Passo: Identificar recursão
2º Passo: Para cada produção com
recursão
2.1: O não terminal que gera a regra de
produção deve receber agora a parte não
recursiva concatenada com um novo não
terminal
A → bA’
2.2: O novo não terminal deve receber a
direita da produção recursiva
concatenada com o próprio novo não
terminal e também a regra gerando vazio
A’ → aA’ | E
Recursividade à Esquerda
(Exemplo 2)

E→E+T|T

T→T*F|F
F → (E) | id

1º Passo: Identificar recursão
Recursividade à Esquerda
(Exemplo 2)





E→E+T|T
T→T*F|F
F → (E) | id
E → TE’
E’ → +TE’ | E
1º Passo: Identificar recursão
2º Passo: Para cada produção com
recursão
2.1: O não terminal que gera a regra de
produção deve receber agora a parte não
recursiva concatenada com um novo não
terminal
E → TE’
2.2: O novo não terminal deve receber a
direita da produção recursiva
concatenada com o próprio novo não
terminal e também a regra gerando vazio
E’ → +TE’ | E
Recursividade à Esquerda
(Exemplo 2)








E→E+T|T
T→T*F|F
F → (E) | id
E → TE’
E’ → +TE’ | E
T → FT’
T’ → *FT’ | E
F → (E) | id
1º Passo: Identificar recursão
2º Passo: Para cada produção com
recursão
2.1: O não terminal que gera a regra de
produção deve receber agora a parte não
recursiva concatenada com um novo não
terminal
T → FT’
2.2: O novo não terminal deve receber a
direita da produção recursiva
concatenada com o próprio novo não
terminal e também a regra gerando vazio
T’ → *FT’ | E