Representação de sólidos

110
Representação de sólidos
Pirâmides e prismas regulares com base(s) contida(s) em planos
verticais ou de topo
Desenhe as projecções de uma pirâmide quadrangular regular, situada no 1.° diedro e com a base
[ABCD] contida num plano vertical d que faz um diedro de 45° (a.d.) com o plano frontal de projecção.
O vértice A tem 1,5 cm de afastamento e 5 cm de cota. O vértice B, consecutivo de A, tem 3 cm de
afastamento e 1 cm de cota. A altura da pirâmide mede 7 cm.
Determinam-se as projecções do quadrado [ABCD] da base da pirâmide recorrendo ao rebatimento do plano d para
o plano frontal de projecção. Em seguida, determinam-se as projecções do centro da base, O, através das diagonais do quadrado. A pirâmide é recta, portanto, o seu eixo [OV] é perpendicular ao plano da base e tem a medida
da altura do sólido. Neste caso, [OV] é um segmento horizontal e projecta-se em verdadeira grandeza, em projecção
horizontal – [O1V1] é perpendicular a hd e mede 7 cm. Determinam-se as projecções do vértice V e desenham-se as
projecções da pirâmide, atendendo às invisibilidades – em primeiro lugar, desenham-se os contornos aparentes
horizontal e frontal. Em projecção frontal, a base é invisível, logo, as arestas [AB] e [AD] (que não pertencem ao contorno aparente frontal) e a aresta lateral [AV] são invisíveis nessa projecção. Em projecção horizontal, as faces laterais
[ABV] e [BCV] são invisíveis, portanto, a aresta [BV] é invisível nessa projecção (note que o vértice B é o de menor
cota da base).
Representação de sólidos
Desenhe as projecções de um cubo, situado no 1.° diedro, sabendo que:
– a face [ABCD] do cubo está contida num plano de topo q que faz um diedro de 60° (a.d.) com o plano
horizontal de projecção;
– o centro dessa face é o ponto O, com 3,5 cm de afastamento e 4 cm de cota;
– a diagonal [AC] é um segmento de topo e o vértice A tem afastamento nulo.
Determinam-se as projecções da face [ABCD] do cubo, recorrendo ao rebatimento do plano de topo q para o plano horizontal de projecção. As arestas do cubo perpendiculares ao plano q são segmentos frontais e projectam-se em verdadeira grandeza em projecção frontal. Estas arestas têm a medida do lado do quadrado [ABCD] (recorde que todas as
arestas do cubo têm o mesmo comprimento). Em seguida, determinam-se as projecções da face [EFGH], paralela a
[ABCD], e desenham-se as projecções do cubo atendendo às invisibilidades – em primeiro lugar, desenham-se os contornos aparentes horizontal e frontal. Em projecção horizontal, a face [EFGH] é visível porque é a face de maior cota do
cubo. A aresta [BF] (de menor cota) e as arestas que convergem no vértice B são invisíveis nessa projecção. Em projecção frontal não há invisibilidades a assinalar – as arestas [AE] e [CG] projectam-se coincidentes, sendo visível [CG] porque tem maior afastamento.
111
112
Representação de sólidos
Desenhe as projecções de um prisma triangular regular, situado no 1.° diedro e com as bases contidas
em planos verticais. O plano vertical b que contém a base [ABC] do prisma faz um diedro de 45° (a.d.)
com o plano frontal de projecção e intersecta o eixo x no ponto de abcissa nula. O vértice A tem 3 cm
de afastamento e 2 cm de cota, e o vértice B tem afastamento nulo e 6 cm de cota. A altura do prisma
mede 7 cm.
Em primeiro lugar, determinam-se as projecções do triângulo equilátero [ABC] da base do prisma recorrendo ao
rebatimento do plano vertical b para o plano frontal de projecção. O prisma é regular, portanto, as suas arestas laterais são perpendiculares aos planos das bases. Neste caso, as arestas laterais são segmentos horizontais e projectam-se em verdadeira grandeza em projecção horizontal. Determinam-se as projecções da base [A’B’C’], paralela a
[ABC], e desenham-se as projecções do prisma, atendendo às invisibilidades. Em projecção frontal, a base [ABC] é
invisível porque é a base de menor afastamento do prisma. As arestas [AB], [BC] e a aresta lateral [BB’] são invisíveis nessa projecção. Em projecção horizontal, apenas a face lateral [BB’C’C] é visível, pelo que a aresta lateral
[AA’] (de menor cota) é invisível nessa projecção.
Desenhe as projecções de uma pirâmide hexagonal regular, situada no 1.° diedro e com a base
[ABCDEF] contida num plano de topo q que faz um diedro de 55° (a.d.) com o plano horizontal de projecção. As arestas da base medem 3,5 cm. O vértice A tem 2,5 cm de cota e a aresta [AB] pertence ao
plano frontal de projecção. O vértice V da pirâmide tem cota nula.
Determinam-se as projecções do hexágono [ABCDEF]
da base da pirâmide recorrendo ao rebatimento do
plano q para o plano horizontal de projecção. A pirâmide é recta, portanto, o seu eixo [OV] é perpendicular
ao plano da base. Neste caso, [OV] é um segmento
frontal e o vértice V tem cota nula – [O2V2] é perpendicular a fq e V2 está no eixo x. Em seguida, desenham-se as projecções da pirâmide, atendendo às
invisibilidades. Em projecção horizontal, a base é visível, pelo que as arestas laterais [AV], [EV] e [FV] são
invisíveis nessa projecção. Em projecção frontal não
há invisibilidades a assinalar – as arestas laterais [AV]
e [EV], [BV] e [DV] projectam-se coincidentes, sendo
visíveis [DV] e [EV] porque têm maior afastamento.
Representação de sólidos
Pirâmides e prismas regulares com base(s) contida(s) em planos
oblíquos, de rampa ou passantes
Plano oblíquo
Desenhe as projecções de uma pirâmide triangular regular, situada no 1.° diedro e com a base [ABC]
contida no plano oblíquo a. Os traços horizontal e frontal do plano a fazem, respectivamente, ângulos
de 45° (a.d.) e 50° (a.d.) com o eixo x e são concorrentes num ponto com 4 cm de abcissa. O centro da
base é o ponto O, com 3,5 de afastamento e 3 cm de cota. O vértice A tem 6 cm de afastamento e 1 cm
de cota. A altura da pirâmide mede 7 cm.
p
V
f0
a
C
fa
O
A
B
x
n0
ha
Determinam-se as projecções do triângulo [ABC] da base da pirâmide recorrendo ao rebatimento do plano oblíquo a
para o plano horizontal de projecção. A pirâmide é regular, portanto, o seu eixo está contido numa recta perpendicular ao plano da base. Pelo ponto O (centro da base) conduz-se a recta p perpendicular ao plano a – as projecções
da recta p são perpendiculares aos traços homónimos do plano. O vértice V da pirâmide pertence à recta p e o eixo
[OV] mede 7 cm (a altura da pirâmide). Como o segmento [OV] não se projecta em verdadeira grandeza em
nenhum dos planos de projecção, recorre-se ao rebatimento do plano q, projectante frontal da recta p, para o plano
frontal de projecção. Determina-se pr definida por Or e Pr (o ponto P é um ponto qualquer da recta). Sobre pr e a partir
de Or marca-se a altura da pirâmide em verdadeira grandeza e obtém-se Vr. Inverte-se o rebatimento e determinam-se
as projecções do vértice V sobre as projecções homónimas da recta p. Desenham-se as projecções da pirâmide,
atendendo às invisibilidades.
113
114
Representação de sólidos
Desenhe as projecções de um prisma triangular regular, situado no 1.° diedro e com as bases contidas
em planos oblíquos, sabendo que:
– uma das bases do prisma é o triângulo [ABC], contido no plano a;
– os traços horizontal e frontal do plano a fazem, respectivamente, ângulos de 60° (a.d.) e 45° (a.d.) com
o eixo x e são concorrentes num ponto com 3 cm de abcissa;
– o lado [AB] do triângulo é frontal (de frente) e tem 1,5 cm de afastamento;
– o vértice A pertence ao b1.3 e o vértice B tem 5 cm de cota;
– a altura do prisma mede 6 cm.
Determinam-se as projecções do triângulo [ABC] da base do prisma contida no plano oblíquo a recorrendo ao rebatimento do plano a para o plano frontal de projecção. O prisma é regular, portanto, as suas arestas laterais estão
contidas em rectas perpendiculares aos planos das bases. Pelos pontos A, B e C conduzem-se rectas perpendiculares ao plano a – as projecções dessas rectas são perpendiculares aos traços homónimos do plano. A altura do
prisma, em projecção, pode ser determinada em qualquer uma das arestas laterais. Considera-se a recta p que contém a aresta lateral [BB’]. Como o segmento [BB’] não se projecta em verdadeira grandeza em nenhum dos planos
de projecção, recorre-se ao rebatimento do plano d, projectante horizontal da recta p, para o plano horizontal de projecção. Determina-se pr definida por Br e Fr (o ponto F é o traço frontal da recta). Sobre pr e a partir de Br marca-se a
altura do prisma em verdadeira grandeza e obtém-se B’r. Inverte-se o rebatimento e determinam-se as projecções
do ponto B’ sobre as projecções homónimas da recta p. A partir das projecções de B’ desenham-se as projecções
das arestas da base [A’B’C’], paralelas às arestas da base [ABC]. Em seguida, desenham-se as projecções do
prisma, atendendo às invisibilidades.
Representação de sólidos
Plano de rampa
Desenhe as projecções de uma pirâmide triangular regular, situada no 1.° diedro e com a base [ABC] contida no plano de rampa q, cujo traço frontal tem 5,5 cm de cota. O centro da base é o ponto O (3,5; 2; 3).
O vértice A tem 6 cm de abcissa e 4,5 cm de cota. A altura da pirâmide mede 7 cm.
Método 1
z
p
f0
p
V
V3
p3
o
O
O3
fO
A
B
O
C
y
x
n0
hO
Em primeiro lugar, determinam-se as projecções do triângulo [ABC] da base da pirâmide recorrendo ao rebatimento do
plano de rampa q para o plano horizontal de projecção. A pirâmide é regular, portanto, o seu eixo está contido numa
recta perpendicular ao plano da base. Pelo ponto O (centro da base) conduz-se a recta p perpendicular ao plano q – a
recta p é de perfil. O vértice V da pirâmide pertence à recta p e o eixo [OV] mede 7 cm (a altura da pirâmide). Como o
segmento [OV] é paralelo ao plano de perfil p0, optou-se por representar a recta p e o plano q em tripla projecção ortogonal. Por O3 conduz-se p3 perpendicular a pq. Sobre p3 e a partir de O3 marca-se a altura da pirâmide em verdadeira grandeza e obtém-se V3. Em seguida, determinam-se as projecções horizontal e frontal do vértice V e desenham-se as projecções da pirâmide, atendendo às invisibilidades.
Método 2
Neste caso, para determinar as projecções do vértice V da pirâmide, conduz-se pela recta p um plano de perfil p e
determina-se a recta de intersecção i dos planos p e q – a recta i é definida pelos seus traços, H’ e F’. As rectas p e i
são perpendiculares no ponto O. Efectua-se o rebatimento do plano p para o plano frontal de projecção e determina-se ir e Or (sobre ir). Por Or conduz-se pr perpendicular a ir. Sobre pr e a partir de Or marca-se a altura da pirâmide e
obtém-se Vr. Inverte-se o rebatimento e determinam-se as projecções do vértice V.
Nota: Verifique que os raciocínios efectuados nos métodos 1 e 2 são muito idênticos. Em ambas as resoluções, para
marcar a altura do sólido, recorre-se a um plano de perfil e ao rebatimento desse plano para o plano frontal de
projecção.
115
116
Representação de sólidos
Desenhe as projecções de um prisma triangular regular, situado no 1.° diedro e com as bases contidas
em planos de rampa. Os pontos A (2,5; 5; 0) e B (6; 2; 2) são dois vértices de uma das bases do prisma.
A altura do sólido mede 6 cm.
Determinam-se os traços do plano de rampa r que contém o triângulo [ABC] da base de menor cota do prisma recorrendo à recta r do plano que contém os pontos A e B. Em seguida, determinam-se as projecções do triângulo recorrendo ao rebatimento do plano r para o plano horizontal de projecção. O prisma é regular, portanto, as suas arestas
laterais estão contidas em rectas perpendiculares aos planos das bases – as arestas laterais são de perfil. A altura do
prisma, em projecção, pode ser determinada em qualquer uma das arestas laterais. Considera-se a aresta [CC’] e a
altura é marcada em verdadeira grandeza em [C3C’3] (ver relatório do exercício anterior / método 1). Determinam-se as
projecções horizontal e frontal do ponto C’ e desenham-se as projecções das arestas da base [A’B’C’], paralelas às
arestas da base [ABC]. Em seguida, desenham-se as projecções do prisma, atendendo às invisibilidades.
Plano passante
Desenhe as projecções de uma pirâmide hexagonal regular, situada no 1.° diedro e com a base contida num plano passante. O centro da base é o ponto O (3,5; 5; 3). As arestas da base medem 3,5 cm e
duas das arestas são paralelas ao eixo x. A altura da pirâmide mede 7 cm.
Em primeiro lugar, determinam-se as projecções do hexágono [ABCDEF] da base da pirâmide recorrendo ao rebatimento do plano passante para o plano frontal de projecção. Recorde que um plano passante é um plano de rampa que
contém o eixo x, pelo que os procedimentos a efectuar na determinação das projecções do vértice V e da pirâmide
seguem os raciocínios expostos no relatório da página anterior / método 1.
117
Exercícios
Representação de sólidos
Base(s) contida(s) em planos verticais ou de topo
135 ✓
Desenhe as projecções de um prisma quadrangular regular, situado no 1.° diedro, sabendo que:
– uma das bases do prisma é o quadrado [ABCD], contido no plano vertical d que faz um diedro de 30° (a.e.)
com o plano frontal de projecção e intersecta o eixo x no ponto de abcissa nula;
– o vértice A tem 1,5 cm de afastamento e cota nula;
– a aresta [AB] mede 5 cm e o vértice B tem afastamento nulo;
– a altura da prisma mede 6 cm.
136
Represente o pentágono regular [ABCDE] contido num plano vertical d. Esta figura é a base de uma pirâmide
pentagonal recta situada no 1.° diedro. Represente igualmente o sólido, assinalando com a convenção gráfica
adequada as arestas invisíveis.
Dados
– o centro da figura é o ponto O (5; 5; 4);
– o plano vertical d intersecta o eixo x na origem das abcissas;
– o vértice A do pentágono está no plano horizontal de projecção e pertence à recta vertical v, que passa
pelo ponto O;
– a pirâmide tem 8 cm de altura.
Baseado na Prova-Modelo (2002)
137
Desenhe as projecções de uma pirâmide triangular regular situada no 1.° diedro, sabendo que:
– o triângulo [ABC] da base está contido no plano de topo g que faz um diedro de 45° (a.e.) com o plano
horizontal de projecção;
– a circunferência circunscrita ao triângulo é tangente ao plano frontal de projecção e o seu centro é o ponto
O (3; 3,5; 3);
– o vértice A tem afastamento nulo;
– a altura da pirâmide mede 7 cm.
138 ✓
Desenhe as projecções de uma pirâmide hexagonal regular situada no 1.° diedro, sabendo que:
– o vértice da pirâmide é o ponto V (– 3; 7; 4);
– o hexágono [ABCDEF] da base está contido no plano vertical d que faz um diedro de 60° (a.e.) com o
plano frontal de projecção e intersecta o eixo x no ponto de abcissa nula;
– as arestas da base medem 3,5 cm e duas das arestas são segmentos verticais.
139 ✓
Desenhe as projecções de um prisma pentagonal regular situado no 1.° diedro, sabendo que:
– as bases do prisma estão contidas em planos verticais que fazem diedros de 45° (a.e.) com o plano frontal
de projecção;
– uma das bases é o pentágono [ABCDE], inscrito numa circunferência com 3,5 cm de raio, cujo centro é o
ponto O (4; 4; 5);
– a face lateral de maior cota do prisma é horizontal (de nível);
– as arestas laterais do sólido medem 5 cm.
118
Representação de sólidos
140
Desenhe as projecções de um prisma hexagonal regular, situado no 1.° diedro e com as bases contidas em
planos de topo, sabendo que:
– os pontos A (– 3; 1; 2) e B (– 5; 0; 5) são dois vértices consecutivos de uma das bases, [ABCDEF], do
prisma;
– a altura do sólido mede 6 cm.
141 ✓
Desenhe as projecções de uma pirâmide quadrangular regular situada no 1.° diedro, sabendo que:
– a base da pirâmide é o quadrado [ABCD], contido num plano de topo;
– os pontos A (0; 7,5; 0) e B (3,5; 9; 3) são os extremos da aresta de maior afastamento da base;
– o vértice V da pirâmide pertence ao b1.3.
Base(s) contidas(s) em planos oblíquos, de rampa ou passantes
142
Desenhe as projecções de uma pirâmide pentagonal regular situada no 1.° diedro, sabendo que:
– o pentágono [ABCDE] da base está contido no plano oblíquo d;
– o plano d é perpendicular ao b1.3 e o seu traço horizontal intersecta o eixo x num ponto com – 8 cm de
abcissa e faz, com esse eixo, um ângulo de 40° (a.e.);
– o pentágono está inscrito numa circunferência com 3 cm de raio e centro no ponto O (3; 4);
– o lado de maior cota do pentágono é horizontal (de nível);
– a altura da pirâmide mede 7 cm.
143 ✓
Desenhe as projecções de um cubo situado no 1.° diedro, sabendo que:
– a face [ABCD] do sólido está contida no plano de rampa q;
– os traços horizontal e frontal do plano q têm, respectivamente, 5 cm de afastamento e 4 cm de cota;
– a diagonal [AC] dessa face é de perfil e tem 4 cm de abcissa;
– o vértice A pertence ao traço frontal do plano q e o vértice C pertence ao traço horizontal do plano.
144
Desenhe as projecções de uma pirâmide hexagonal regular, situada no 1.° diedro e com a base [ABCDEF]
contida no plano oblíquo a, sabendo que:
– os traços horizontal e frontal do plano a fazem, respectivamente, ângulos de 55° (a.d.) e 45° (a.d.) com o
eixo x e são concorrentes num ponto com 3 cm de abcissa;
– os pontos A (2; 4) e D são os extremos de uma diagonal maior do hexágono da base;
– a diagonal [AD] é horizontal (de nível) e mede 6 cm;
– o vértice V da pirâmide tem cota nula.
145
Desenhe as projecções de um paralelepípedo rectângulo situado no 1.° diedro, sabendo que:
– a face [ABCD] do sólido está contida no plano de rampa r cujos traços horizontal e frontal têm, respectivamente, 5 cm de afastamento e 4 cm de cota;
– o vértice A tem 4,5 cm de abcissa e afastamento nulo;
– a aresta [AB] dessa face faz um ângulo de 30° com o traço frontal do plano r e o vértice B tem abcissa nula;
– a aresta [BC] mede 3 cm;
– as arestas de perfil do paralelepípedo medem 6 cm.
Representação de sólidos
146 ✓
Desenhe as projecções de um prisma pentagonal regular situado no 1.° diedro, sabendo que:
– uma das bases do prisma é o pentágono [ABCDE], contido no plano de rampa q, cujo traço frontal tem 5 cm
de cota;
– o plano q faz um diedro de 50° com o plano frontal de projecção e o seu traço horizontal tem afastamento
positivo;
– o centro da base [ABCDE] é o ponto O, com 3 cm de abcissa e 2,5 cm de cota;
– o vértice A tem abcissa nula e 2,5 cm de cota;
– a altura do prisma mede 6 cm.
147 ✓
Desenhe as projecções de um cubo situado no 1.° diedro, sabendo que:
– a face [ABCD] do sólido está contida no plano oblíquo d;
– os pontos A (1,5; 0; 4,5) e B (0; 3; 1) são os extremos de uma aresta dessa face;
– o traço frontal do plano d faz um ângulo de 50° (a.d.) com o eixo x.
148
Desenhe as projecções de uma pirâmide quadrangular regular, situada no 1.° diedro e com a base contida
num plano oblíquo a, sabendo que:
– os pontos A (0; 1,5; 3) e B (– 2,5; 5; 1) são dois vértices do quadrado [ABCD] da base do sólido;
– a aresta [AB] está contida numa recta de maior inclinação do plano a;
– a altura da pirâmide mede 7 cm.
149 ✓
Desenhe as projecções de um cubo situado no 1.° diedro, sabendo que:
– a face [ABCD] do sólido está contida num plano passante;
– o centro dessa face é o ponto O (4; 6; 3);
– o vértice A tem 1 cm de abcissa e 4,5 cm de afastamento.
150 ✓
Desenhe as projecções de uma pirâmide quadrangular regular, situada no 1.° diedro e com a base contida
num plano passante, sabendo que:
– o ponto A (1; 3; 2) é o vértice de menor abcissa do quadrado [ABCD] da base da pirâmide;
– a diagonal [AC] do quadrado mede 7 cm e está contida numa recta que faz um ângulo de 30° com o eixo x;
– o vértice V da pirâmide pertence ao plano frontal de projecção.
151 ✓
Desenhe as projecções de uma pirâmide quadrangular regular com a base contida num plano oblíquo, sabendo
que:
– o vértice da pirâmide é o ponto V (–3; 7; 9);
– o ponto O (2; 4; 3) é o centro da base;
– as diagonais da base medem 6 cm e uma das diagonais é horizontal (de nível).
152
Desenhe as projecções de um prisma triangular regular situado no 1.° diedro, sabendo que:
– uma das bases do prisma é o triângulo [ABC], contido no b1.3;
– o vértice A tem 4 cm de abcissa e 3 cm de afastamento;
– o lado [AB] do triângulo está contido numa recta que faz um ângulo de 50° com o eixo x e o vértice B tem
abcissa nula;
– o segmento [AD] é uma das arestas laterais do sólido e o vértice D pertence ao plano frontal de projecção.
119
120
Representação de sólidos
Exercício
135
Determinam-se as projecções do quadrado [ABCD] da base do prisma recorrendo ao rebatimento do plano vertical d
para o plano frontal de projecção. Note que o vértice A tem cota nula, portanto, pertence a hd e o vértice B tem afastamento nulo, logo, pertence a fd. Sabe-se que [AB] mede 5 cm, assim, com centro em Ar desenha-se um arco de
circunferência de raio igual a 5 cm. O ponto de intersecção desse arco com fd é Br ∫ B2 (o ponto B pertence à charneira do rebatimento, portanto, mantém-se fixo). Constrói-se o quadrado em verdadeira grandeza no rebatimento e,
em seguida, determinam-se as suas projecções. As projecções do prisma são determinadas de acordo com os procedimentos expostos na página 112. Verifique que a aresta lateral [AA’] (invisível em projecção horizontal) está contida no plano horizontal de projecção.
Exercício
138
Desenham-se as projecções do vértice V e representam-se os traços do plano vertical d que contém a base da pirâmide. Em seguida, determinam-se as projecções do centro da base O – a pirâmide é regular, portanto, o seu eixo
[OV] é perpendicular ao plano da base. Neste caso, [OV] é um segmento horizontal e o ponto O pertence ao plano d
– [O1V1] é perpendicular a hd e O1 está sobre hd. Para determinar as projecções do hexágono [ABCDEF] da base
optou-se pelo rebatimento do plano d para o plano frontal de projecção. Em seguida, desenham-se as projecções da
pirâmide, atendendo às invisibilidades. Em projecção frontal, a base é invisível, pelo que as arestas [AB], [BC] e
[CD] (que não pertencem ao contorno aparente frontal) e as arestas laterais [BV] e [CV] são invisíveis nessa projecção. Em projecção horizontal não há invisibilidades a assinalar.
Representação de sólidos
Exercício
139
Determinam-se as projecções do pentágono [ABCDE] da base do prisma recorrendo ao rebatimento do plano vertical b
para o plano frontal de projecção. Note que a face lateral de maior cota do prisma está contida num plano horizontal,
portanto, o lado de maior cota do pentágono é um segmento horizontal. As projecções do prisma são determinadas
de acordo com os procedimentos expostos na página 112. Em projecção frontal, a base [ABCDE] é invisível pois é a
base de menor afastamento do sólido. As arestas [AE], [DE] e a aresta lateral [EE’] são invisíveis nessa projecção. Em
projecção horizontal, as faces laterais [AA’B’B] e [AA’E’E] são invisíveis, pelo que a aresta lateral [AA’] (de menor
cota) é invisível nessa projecção.
Exercício
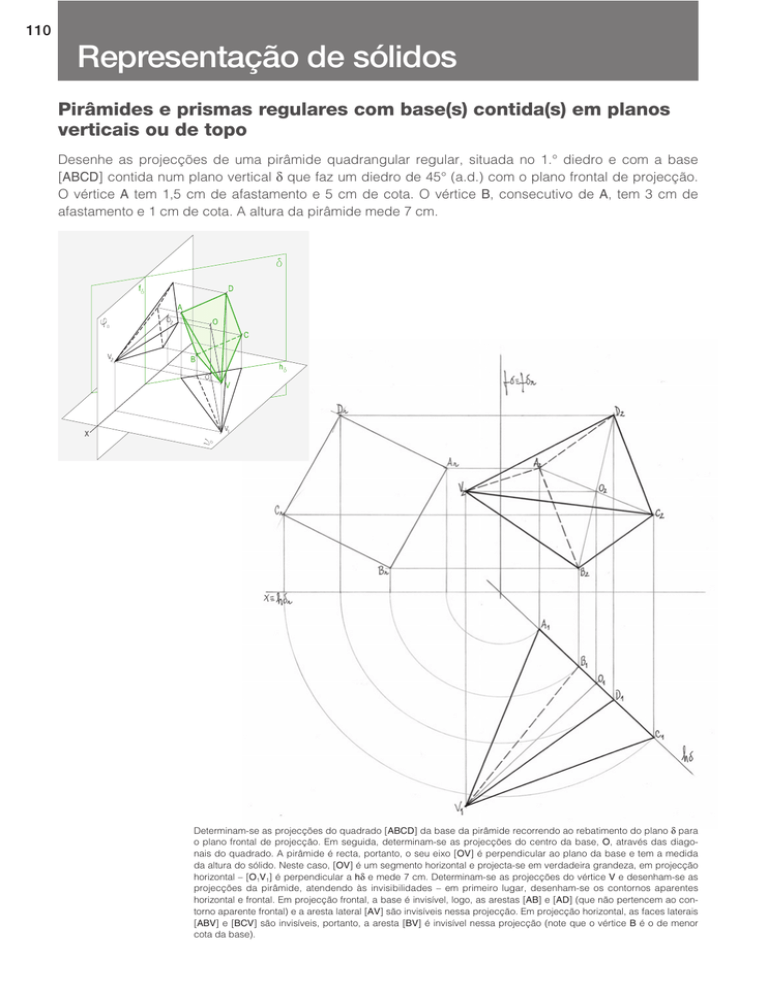
141
Para determinar as projecções do quadrado [ABCD] da base optou-se pelo rebatimento do plano q para o plano
horizontal de projecção. Em seguida, determinam-se as projecções do centro da base, O, através das diagonais do
quadrado. O eixo [OV] da pirâmide é um segmento frontal, perpendicular ao plano da base, e o vértice V pertence
ao b1.3, portanto, o ponto V é o traço no b1.3 da recta frontal que contém o eixo (as projecções de V são simétricas em
relação ao eixo x). Desenham-se as projecções da pirâmide atendendo às invisibilidades. Em projecção horizontal, a
base é invisível, logo, a aresta [AD] é invisível nessa projecção. Em projecção frontal, as faces laterais [ADV] e
[CDV] são invisíveis, pelo que a aresta [DV] é invisível nessa projecção (note que o vértice D é o de menor afastamento da base).
121
122
Representação de sólidos
Exercício
143
Em primeiro lugar, determinam-se as projecções do quadrado [ABCD] recorrendo ao rebatimento do plano de rampa q
para o plano frontal de projecção. As projecções do cubo são determinadas de acordo com os procedimentos expostos na página 116. Recorde que todas as arestas do sólido têm o mesmo comprimento; assim, considera-se a aresta
[BF] e transporta-se a medida do lado do quadrado [ABCD] (obtida em verdadeira grandeza no rebatimento) para
[B3F3].
Exercício
146
Em primeiro lugar, representa-se o plano de rampa q em tripla projecção ortogonal. Para as projecções do pentágono [ABCDE] da base do prisma contida no plano q, ver relatório do exercício 130. As projecções do prisma são
determinadas de acordo com os procedimentos expostos na página 116.
Representação de sólidos
Exercício
147
Em primeiro lugar, determinam-se os traços do plano oblíquo d recorrendo à recta r que contém a aresta [AB] do
cubo – r está contida no plano d, portanto, fd contém o vértice A (o ponto A pertence ao plano frontal de projecção) e
hd contém o traço horizontal da recta r e é concorrente com fd no eixo x. O processo de resolução segue os procedimentos expostos na página 114. Recorde que todas as arestas do cubo têm o mesmo comprimento. Considera-se a
recta p que contém a aresta [CG] e recorre-se ao rebatimento do plano q, projectante frontal da recta p, para o plano
frontal de projecção. Determina-se pr definida por Cr e Fr (o ponto F, traço frontal da recta, pertence à charneira, portanto, mantém-se fixo). Sobre pr e a partir de Cr marca-se a medida da aresta (obtida em verdadeira grandeza no
rebatimento da face [ABCD]) e obtém-se Gr. Inverte-se o rebatimento e determinam-se as projecções do ponto G
sobre as projecções homónimas da recta p. A partir das projecções de G desenham-se as projecções das arestas
da face [EFGH], paralelas às arestas da face [ABCD]. Em seguida, desenham-se as projecções do cubo, atendendo
às invisibilidades.
123
124
Representação de sólidos
Exercício
149
Em primeiro lugar, determinam-se as projecções do quadrado [ABCD] recorrendo ao rebatimento do plano passante
para o plano frontal de projecção. As projecções do cubo são determinadas de acordo com os raciocínios expostos
na página 116. Recorde que todas as arestas do sólido têm o mesmo comprimento; assim, considera-se a aresta [AE]
e transporta-se a medida do lado do quadrado [ABCD] (obtida em verdadeira grandeza no rebatimento) para [A3E3].
Exercício
150
Ver página 116. O vértice V da pirâmide pertence ao plano frontal de projecção, portanto, tem afastamento nulo –
em projecção de perfil, V3 situa-se no eixo z.
Representação de sólidos
Exercício
151
Em primeiro lugar, desenham-se as projecções do eixo [OV] da pirâmide. A pirâmide é regular, portanto, o plano a
que contém o quadrado da base é perpendicular à recta r que contém o eixo [OV] do sólido. Os traços do plano a
são perpendiculares às projecções homónimas da recta r e para a sua determinação recorre-se à recta horizontal h
que contém o ponto O e é perpendicular à recta r. As projecções do quadrado [ABCD] da base da pirâmide são
determinadas recorrendo ao rebatimento do plano a para o plano horizontal de projecção – note que uma das diagonais é horizontal, portanto, está contida na recta h. Em seguida, desenham-se as projecções da pirâmide, atendendo
às invisibilidades.
125