Enviado por
common.user11258
ATIVIDADE 01 - 7º ANO - IMPRESSAS (1)

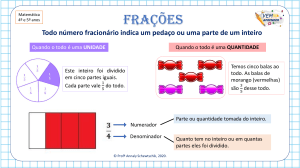
GOVERNO DO ESTADO DO ACRE SECRETARIA DE ESTADO DE EDUCAÇÃO, CULTURA E ESPORTE ESCOLA FREI HEITOR MARIA TURRINI Caderno de Atividades a Distância 1° BIMESTRE 7° ANOS D ESCOLA: FREI HEITOR MARIA TURRINI DISCIPLINA: MATEMÁTICA PROFESSORA: ALLLAN KARDEC NOME DA(O) ALUNA(O): ___________________________________________________________ SÉRIE/TURMA: ____________ DATA: ___/___/2021 ATENÇÃO!!! Você deve fazer a LEITURA dos textos e RESOLVER AS ATIVIDADES de acordo com as orientações dadas pelo professor de cada disciplina. As atividades estão sendo avaliadas. Portanto, no retorno às aulas essas atividades deverão ser entregues aos professores para correção e atribuição de notas e/ou conceitos para os Bimestres. Olá querida(o) aluna(o)!!! Eu me chamo Allan Kardec Oliveira, tenho 40 anos e sou professor de Matemática na Escola Frei Heitor Maria Turrini. E neste Ano Letivo de 2021, é com muita ALEGRIA que serei seu professor de Matemática. Que todos vocês sejam bem-vindos. Sendo assim vamos trabalhar juntos para garantir o melhor ensino/aprendizagem de vocês. Desejo um excelente Ano Letivo!!! Responda abaixo algumas perguntas que me ajudará a conhecer você melhor. 1° - Qual o seu nome? ___________________________________ 2° - Qual a sua idade? _______ 3° - Me conta uma ou mais qualidades sua. _____________________________________________ ________________________________________________________________________________ 4° - Agora me fala algo que você considera um defeito. ________________________________________________________________________________ 5° - Me fala seu hobby preferido (uma atividade de lazer, um passatempo). ________________________________________________________________________________ 6° - Agora me conta um sonho seu. Algo que deseja realizar. ________________________________________________________________________________ 7º - O que você mais gosta e o que menos gosta de estudar na disciplina de matemática. ________________________________________________________________________________ ________________________________________________________________________________ ORIENTAÇÕES Leia atentamente toda a atividade; Nessa atividade, temos todo o conteúdo que você irá estudar no 1º bimestre do Ano Letivo de 2021. Estude os conteúdos e depois resolva a atividade no final desse material. Está atividade valerá como nota para o fechamento do bimestre. Por isso, se empenhe ao máximo. BONS ESTUDOS!!! ATIVIDADE LEIA, COM ATENÇÃO, OS CONTEÚDOS ABAIXO. CONTEÚDO 01: Operações com números naturais Você se lembra o que são os números naturais? Os números naturais são aqueles que utilizamos para indicar uma contagem, uma medida, uma ordem ou um código. POR EXEMPLO: Ana comprou 12 pães. (o número natural 12 foi utilizado para indicar uma contagem, isto é, a quantidade de pães que Ana comprou) OUTRO EXEMPLO: Marcos ficou em 3º lugar na Olimpíada de Matemática de sua escola. (foi utilizado o número natural 3 para indicar uma ordem) MAIS UM EXEMPLO: Dona Olinda subiu em uma balança e constatou que está pesando 59 kg. (o número 59 foi utilizado para indicar uma medida) Agora, vamos utilizar os números naturais para realizar operações. Como você já conhece as quatro operações básicas de Matemática (Adição, Subtração, Multiplicação e Divisão), vamos resolver alguns exemplos abaixo. Aproveite e copie esses exemplos em seu caderno. EXEMPLO 01: Lucas tinha R$ 385,00 depositado na conta bancária. Ele, então, retirou R$ 145,00 e, dessa quantia, separou R$ 87,00 para comprar um sapato em uma loja. a) Quanto restou na conta bancária de Lucas? RESPOSTA: Para verificar quanto restou na conta bancária de Lucas após ele retirar R$ 145,00, precisamos realizar uma operação de SUBTRAÇÃO. , logo ainda restou R$ 240,00 b) Quanto ainda ficou da parte que ele retirou da conta? RESPOSTA: Como Lucas retirou R$ 145,00 e comprou um sapato desse dinheiro no valor de R$ 87,00, vamos calcular a SUBTRAÇÃO , assim, ele ainda ficou com R$ 58,00. EXEMPLO 02: Ana Carolina tinha 160 peças de roupa no armário. Ela separou uma parte dessas roupas que não ia usar mais e deu 15 peças para a mãe, vendeu 27 para um brechó e reservou 11 para a campanha de doação de roupas de inverno. Quantas peças de roupa restaram no armário de Ana Carolina? RESPOSTA: Vamos calcular primeiro as peças de roupas que ela deu para a sua mãe, para o brechó e para doação: . Agora, vamos calcular quantas peças restaram. , Ana Caroline ainda ficou com 107 peças. EXEMPLO 03: Joana precisava comprar um carro e não tinha todo o dinheiro para o pagamento à vista. Assim, ela deu R$ 10.000,00 de entrada e dividiu o restante em 12 parcelas de R$ 1.570,00. Qual o valor total do carro? RESPOSTA: Temos: Vamos calcular quanto ela vai pagar na parte parcelada: Assim, Joana pagará pelo carro EXEMPLO 04: Francisco comprou uma impressora e um teclado, como os representados abaixo, e pagou a compra em 8 parcelas iguais e sem acréscimos. Qual o valor de cada parcela? RESPOSTA: Primeiro, temos que somar os preços dos produtos que Francisco comprou. Agora, vamos parcelar R$ 376,00 em 8 vezes. Para isso precisamos fazer uma divisão. Vamos lá!! CONTEÚDO 02: Os Números Racionais 1° MOMENTO – Representações dos Números Racionais Você lembra como são formados os números racionais? Os números racionais podem ser representado por um número em forma de FRAÇÃO ou por um número DECIMAL. A FRAÇÃO é um número que representa parte de um todo ou inteiro. Observe, no exemplo, que o quadrado foi dividido em 4 partes, dessas partes foram pintadas 3. Então, para montar a fração, o número colocado embaixo do traço é o denominador e indica a quantidade de partes que o todo ou inteiro foi dividido. Já o número em cima do traço é o numerador e indica a quantidade de partes do todo ou inteiro que estão sendo considerados. Os NÚMEROS DECIMAIS são aqueles expressos com vírgula. Nesses números, a virgula separa a parte inteira da parte decimal. 2° MOMENTO – Operações com Números Racionais na forma fracionária ADIÇÃO E SUBTRAÇÃO DE FRAÇÕES Com denominadores IGUAIS ADIÇÃO → Repete o denominador e soma os SUBTRAÇÃO → Repete o denominador e subtrai numeradores. (Ex.) os numeradores. (Ex.) Com denominadores DIFERENTES: Operações com frações que envolva somar ou subtrair frações com denominadores diferentes, devemos primeiro reduzi-las a um mesmo denominador. Para isso, calculamos o MMC dos denominadores. ADIÇÃO (Ex.) SUBTRAÇÃO (Ex.) Podemos verificar as frações equivalentes a Vamos achar as frações equivalentes a essas essas duas frações, encontrando as que têm duas frações, encontrando as que têm mesmo mesmo denominador. denominador. Agora, que encontramos duas frações Agora, vamos resolver a subtração: equivalentes as iniciais, mas com denominadores iguais, vamos resolver a adição: Também podemos reduzir as frações ao mesmo denominador utilizando o mínimo múltiplo comum (MMC) dos denominadores. Calculando o MMC (3, 9) = 9 Agora, adicionamos as frações com mesmo denominador. MÉTODO BORBOLETA Veja como calcula utilizando o método borboleta Também é conhecida como cruzadinha. A ideia é multiplicar os denominadores, achando o valor do denominador da resposta. Posteriormente, deve-se multiplicar o denominador da segunda fração pelo numerador da primeira fração, colocando a resposta no numerador; em seguida, manter o sinal da fração e multiplicar o denominador da primeira fração pelo numerador da segunda, fazendo uma multiplicação cruzada ou em formato de borboleta. Então, soma-se ou subtrai esses valores. MULTIPLICAÇÃO DE FRAÇÕES A multiplicação entre frações consiste em multiplicar numerador com numerador e, em seguida, denominador com denominador delas. De forma geral, a multiplicação fica assim: Ex.: DIVISÃO DE FRAÇÕES Na divisão de fração, devemos conservar (manter) a primeira fração e multiplicá-la pelo inverso da segunda. Sua forma geral fica da seguinte maneira: Ex.: CONTEÚDO 03: Cálculo de Porcentagem Utiliza-se o símbolo % (por cento) à direita de um número para indicar sua forma percentual. Por exemplo: 25% e 10% estão na forma percentual. A porcentagem é uma fração cujo denominador (a parte de baixo), é 100. Por isso falamos 'por cento'. Como calcular porcentagem??? Há diversos métodos para cálculos de porcentagem. Todos chegam ao mesmo resultado. O importante é encontrar a maneira que faça mais sentido para você e para a situação. Vamos ver essas formas e peço que copie esses exemplos em seu caderno. Calcular porcentagem como fração (divisão e multiplicação) Exemplo: Imagine que você tenha lido em um noticiário que a taxa de letalidade da covid-19 é de 3%. Isso significa que, a cada 100 pessoas diagnosticadas com a doença, espera-se que 3 delas venham a morrer. Vamos supor que 800 pessoas da certa cidade contraíram o vírus. Qual o número esperado de mortes? RESPOSTA: Vamos calcular quanto é 3% de 800 pessoas. Sabendo que a porcentagem 3% pode ser transformado em uma fração. Então, podemos multiplicar 800 × 3, e depois Logo, o número esperado de mortes é de 24 pessoas dividir o resultado por 100. Veja ao lado → Calcular porcentagem como decimal (fator multiplicativo) Exemplo: Imagine que um sapato que custava R$ 150 está em promoção com 30% de desconto. Qual será sua economia? RESPOSTA: Calculando Logo, a economia na compra do sapato é de Agora, vamos multiplicar 0,3 com o valor do R$ 45,00. sapato sem o desconto. Veja ao lado → Calcular a porcentagem na calculadora Exemplo: Vamos calcular quanto é 64% de 200 utilizando a calculadora. RESPOSTA: Para calcular porcentagem na calculadora, digite em sua calculadora logo terá o resultado e . CONTEÚDO 04: Múltiplos e divisores de um número natural MÚLTIPLOS DE UM NÚMERO: Os múltiplos de um número são obtidos multiplicando o número por um fator. Este fator, por sua vez, é também divisor do múltiplo encontrado. Exemplo: Veja os múltiplos do número 6, é o resultado da multiplicação do número 6 por qualquer outro número natural. Multiplicação 6 x 0 6 x 1 6 x 2 6 x 3 6 x 4 6 x 5 6 x 6 6 x 7 6 x 8 Múltiplos 0 6 12 18 24 30 36 42 48 6x9 54 ... ... Assim, os múltiplos de 6 são (0, 6, 12, 18, 24, 30, 36, 42, 48, 54, ...) Exemplo: Veja os múltiplos de outros números. a) b) c) DIVISORES DE UM NÚMERO: Um número é divisor do outro quando não há resto na divisão. Observe os exemplos. Divisão de 40 por 5. Veja que a divisão de 40 por 5 tem resto zero, então é uma divisão exata. Logo, 5 é divisor de 40. Divisão de 40 por 7. Já a divisão de 40 por 7 tem resto diferente de zero. Então a divisão não é exata. Logo, 7 não é divisor do 40. CONTEÚDO 05: Unidades de Medidas Vamos lembrar as unidades de medidas que utilizamos no nosso dia a dia. UNIDADES DE MEDIDAS GRANDEZAS SUBMÚLTIPLOS MÚLTIPLOS PADRÃO COMPRIMENTO: utilizada quilômetro (km), decímetro (dm), para medir algo. Suas metro hectômetro (hm), centímetro (cm), unidades são usadas de m decâmetro (dam) milímetro (mm) acordo com a necessidade. CAPACIDADE: é a medida de quilolitro (kl), decilitro (dl), líquidos, gás ou outra litro hectolitro (hl), centilitro (cl), substância que um recipiente l decalitro (dal) mililitro (ml) pode conter. MASSA: é a medida que indica a quantidade de matéria em um corpo. A unidade de medida padrão de massa é o quilograma (kg). Uma unidade bastante utilizada é o grama. quilograma (kg), hectograma (hg), decagrama (dag) grama g decigrama (dg), centigrama (cg), miligrama (mg) INSTRUMENTOS DE MEDIÇÃO Régua, fita métrica, trena, micrômetro, paquímetro Recipientes como xicaras, copos, colheres etc Balança digital, de pratos, de precisão e mecânica Outras unidades de massa: 1 Tonelada (t) = 1000 kg e 1 arroba (@) = 15 kg TEMPO Medir o tempo é de fundamental importância para a organização das atividades cotidiana. A unidade padrão de tempo é o segundo (s). Também temos outras unidades como: minutos (min) e horas (h). Dia, semana, mês, ano, década, século, milênio. Relógios analógicos (de ponteiros) e digital, calendários Vamos estudar agora alguns EXEMPLOS envolvendo unidades de medida. Aproveite e copie eles em seu caderno. EXEMPLO 01: Uma creche atende diariamente 15 crianças. Durante o tempo em que as crianças ficam na creche, cada uma delas toma 3 mamadeiras de leite. Se cada mamadeira tem 250 ml, quantos litros de leite as crianças tomam por dia? RESPOSTA: Observe que, se cada criança toma 3 mamadeiras de leite e cada mamadeira tem capacidade de 250 ml, então durante o dia cada criança toma 3 x 250 ml = 750 ml de leite. Como a creche atende 15 crianças, temos que 15 x 750 ml = 11.250 ml, que equivalem a 11 litros e 25 ml. EXEMPLO 02: Jair e seus amigos foram pescar no último final de semana prolongado. Para chegar ao pesqueiro, percorreram 8 km de carro, 700 m a pé e 2,5 km de barco. A distância total, em metros, que eles percorreram para ir e voltar da pescaria foi de RESPOSTA: Como a questão pede a distância percorrida em metros, vamos, primeiramente, converter cada distância percorrida para metro. 8 km de carro 700 m a pé 2,5 km de barco 8 km é igual a 8.000 m Já está OK 2,5 km é igual a 2.500 m Assim, a distância percorrida para ir a pescaria 8.000 + 700 + 2.500 = 11.200 m Considerando que para voltar é a mesma distância, então o total é 11.200 + 11.200 = 22.400 m. EXEMPLO 03: Uma peça de teatro teve início às 20h 30min. Sabendo que a mesma teve duração de 105 minutos, qual é esse tempo da peça em horas? RESPOSTA: Sabemos que 1 hora é igual a 60 minutos. Então o tempo de duração dessa peça é 60 min + 45 mim que equivale a 1 hora e 45 min. CONTEÚDO 06: Ângulos 1º MOMENTO: Ideia de ângulos Ângulo é a região de um plano limitada por duas semirretas de mesma origem. Os ângulos são importantes em muitas atividades humanas. Aparecem na construção civil, nos relógios de ponteiros, nas falas de comentaristas de futebol ao comentar a posição da bola em relação ao gol etc. Veja os exemplos abaixo. Aproveite e copie eles em seu caderno. EXEMPLO 01: O movimento completo do limpador do para-brisa de um carro corresponde a um ângulo raso (mede 180º). Na situação descrita pela figura, admita que o limpador está girando em sentido horário. Calcule a medida do ângulo que falta para que ele complete o movimento completo. RESPOSTA: O para-brisa, movendo-se em sentido horário, já se movimentou 40º, se o total é 180º, temos (A) 50º (B) 120º (C) 140º (D) 160º EXEMPLO 02: Para chegar à escola, Carlos realiza algumas mudanças de direção como mostra a figura a seguir: As mudanças de direção que formam ÂNGULOS RETOS (90º) estão representadas nos vértices: (A) B e G. (B) D e F. (C) B e E. (D) E e G. RESPOSTA: Duas mudanças de direção formam um ângulo de 90º graus: E e G. 2º MOMENTO: Classificação e medidas de ângulos Classificação de ângulos quanto à sua medida. CONTEÚDO 07: Polígonos 1º MOMENTO: Definição de Polígono A palavra polígono é utilizada para representar a região poligonal (superfície plana limitada pelos segmentos), como a imagem ao lado. Polígono é uma figura geométrica plana, fechada, formada por segmento de reta que não se cruzam e delimitam a região poligonal. Veja os elementos dos polígonos. Alguns polígonos recebem nomes especiais, de acordo com o número de ângulos (ou de lados) que apresentam. Veja: 2º MOMENTO: Triângulos Classificação dos triângulos com relação às medidas de seus lados e de seus ângulos Triângulo equilátero Quanto aos lados Triângulo isósceles 3 lados congruentes 2 lados congruentes Triângulo escaleno Triângulo acutângulo 3 lados com medidas diferentes 3 ângulos agudo Quanto aos ângulos Triângulo Triângulo retângulo obtusângulo 1 ângulo reto 1 ângulo obtuso CONTEÚDO 08: Prismas e Pirâmides Os prismas e as pirâmides são sólidos geométricos, vamos ver um pouco sobre as características desses sólidos. Note que os PRISMAS possuem duas bases enquanto a PIRÂMIDE só possui uma base. Essas bases podem ser qualquer figura geométrica plana. Os nomes dos prismas e das pirâmides são dados de acordo com a figura plana de sua BASE, que pode ser triangular, quadrangular, retangular, pentagonal e etc. Veja alguns prismas e pirâmides e suas características: SÓLIDO FACES N° DE N° DE N° DE NOME BASE GEOMÉTRICO LATERAIS FACES ARESTAS VÉTICES Pirâmide de base triangular Ou Tetraedro Triângulo Triângulos 4 6 4 Pirâmide de base quadrada Quadrado Triângulos 5 8 5 Pirâmide de base pentagonal Pentágono Triângulos 6 10 6 Pirâmide de base hexagonal Hexágono Triângulos 7 12 7 Prisma de base triangular Triângulos Retângulos 5 9 Prisma de base quadrangular Quadrados Retângulos 6 12 8 Prisma de base pentagonal Pentágonos Retângulos 7 15 10 Prisma de base hexagonal Hexágonos Retângulos 8 18 12 6 ATIVIDADE De acordo com o que estudamos acima, resolva as seguintes questões. QUESTÃO 01: Quantos anos você fará em 2030? ________________________________________ QUESTÃO 02: Uma caixa de média de lápis contém 6 dúzias de lápis. A caixa maior contém exatamente o triplo. A quantidade de lápis da caixa maior é: (A) 18 lápis. (B) 72 lápis. (C) 180 lápis. (D) 216 lápis. QUESTÃO 03: Para encher uma piscina, que estava totalmente vazia, foi utilizada uma torneira que despejava 300 L de água por minuto. a) Quantos litros de água foram despejados na piscina após 7 min? E após 1 h? ________________________________________________________________________________ ________________________________________________________________________________ b) Sabendo que a piscina foi completamente cheia após 1 h 35 min, qual a medida da capacidade, em litros, dessa piscina? ____________________________________________________________ ________________________________________________________________________________ QUESTÃO 04: Um atleta maratonista profissional percorre todos os dias em treinamento 20.000 metros. Por semana, esse atleta percorre quantos quilômetros? (A) 140.000 km (B) 100 km (C) 100.00 km (D) 140 km QUESTÃO 05: Qual o resultado de (A) (B) (C) ? (D) QUESTÃO 06: Os vértices do triângulo representado no plano cartesiano ao lado são: (A) (B) (C) (D) A(5, -2); A(2, -5); A (-2, 5); A(-3, 0); B(1, -3) e C(4, 3) B(-3, -1) e C( 3, -4) B(-3, 1) e C(3, 4) B(-2, 0) e C(3, 0) QUESTÃO 07: Considere os sólidos geométricos ao lado e responda: a) Observando a base do prisma e a base da pirâmide, o que existe de comum entre elas? ________________________________________________________________ b) Quais os nomes que esses sólidos geométricos recebem? _____________________________________________________________________ _____________________________________________________________________ c) Elabore, no espaço abaixo, uma tabela que contenha a quantidade de arestas, a quantidade de vértices e também o número de faces desses sólidos. QUESTÃO 08: Simone fez o desenho a seguir para representar o trajeto de sua casa ao parque indicando os ângulos que realiza no percurso. Nesse desenho, o ângulo reto é encontrado no vértice identificado pela letra (A) A. (B) B. (C) C. (D) D. QUESTÃO 09: Lucas tem uma dívida de R$ 5 000,00 com o banco. Este mês, ele conseguiu pagar 30% dessa dívida. Qual foi a quantia dessa dívida paga por Lucas ao banco neste mês? (A) R$ 30,00 (B) R$ 50,00 (C) R$ 1 500,00 (D) R$ 3 500,00 QUESTÃO 10: Observe no quadro abaixo a promoção de uma loja de calçados. Ao comprar esse tênis à vista, o valor do desconto oferecido por essa loja é de (A) R$ 250,00 (B) R$ 150,00 (C) R$ 50,00 (D) R$ 15,00 Pronto! Chegamos ao final da atividade. Agora, você poderá responder segundo as instruções que lhe foi dada e, depois de resolver, entrega-la lá na escola. BONS ESTUDOS!!! Sucesso é o acúmulo de pequenos esforços repetidos dia a dia. - Robert Collier O Senhor os abençoe e os guarde; - Nm 4: 24