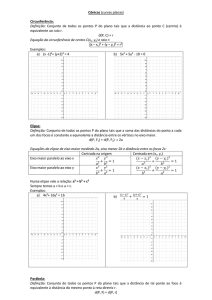
1) A equação de 2º grau com duas variáveis representa uma cônica: Ax² + Bxy + Cy² + Dx + Ey + F = 0 Se: B² - 4AC = 0 ⇒ PARÁBOLA B² - 4AC > 0 ⇒ HIPÉRBOLE B² - 4AC < 0 ⇒ ELIPSE B = 0 e A = C ⇒ CIRCUNFERÊNCIA (Infelizmente, no Brasil, é o nome dado ao CÍRCULO) 2) Para determinar que tipo de curva cada equação representa devemos observar algumas características das equações, observe: Reta: x e y possuem expoentes iguais a 1, sendo que nem x, nem y podem estar no denominador, nesse caso item (II) Circunferência: o número que multiplica x² e y² é sempre o mesmo e temos uma soma de x² e y² nesse caso o item (V) Elipse: os números que multiplicam x² e y² são diferentes e temos uma soma de x² e y², item (I) Hipérbole: temos uma subtração de x² e y², item (IV) Parábola: temos só x² ou só y², item (III) 3) x²/4 - y²/9 = 1 ---> x²/2² - y²/3² = 1 Temos a equação de uma hipérbole com eixo real a = 2 e eixo imaginário ou eixo conjugado b = 3 As duas retas que passam pela origem e são assintóticas à hipérbole são y = (3/2).x e y = (-3/2).x Logo, as retas que não interceptam a hipérbole são: y = m.x, |m| > 3/2 ou x = 0 (eixo y) 4) Pelos dados 2a-2b = b, logo a = 3b/2. Substituindo no V = 4(3b/2)b² = 6b³. 5) 9x²-4y²-18x-16y-43 =0 Complete quadrados: (9x² - 18x + 9) - (4y² -16y -16) = 43 + 9 -16 9(x² -2x + 1) - 4(y² +4y + 4) = 36 9(x - 1)² - 4(y + 2)² = 36 Divida tudo por 36 [9(x - 1)²]/36 - [4(y + 2)²]/36 = 36/36 (x - 1)²/4 - (y + 2)²/9 = 1 (equação reduzida da hipérbole) a² = 4 ⇔ a = 2 b² = 9 ⇔ b = 3 Centro da Hipérbole é C(1,-2) Eixo Real medindo 2a = 4 Eixo Imaginário medindo 2b = 6 Assíntotas y1 e y2: (passam pelo centro C) y - yC = m (x - xC) y - 1 = m (x + 2) m1 = b/a = 3/2 m2 = -b/a = -3/2 y1 - 1 = 3/2(x + 2) y1 = 3/2 x + 4 y2 - 1 = 3/2(x + 2) y2 = -3/2 (x + 2) + 1 y2 = -3/2 x -3 + 1 y2 = -3/2 x -2] 6) 1) V 2) V 3) V
