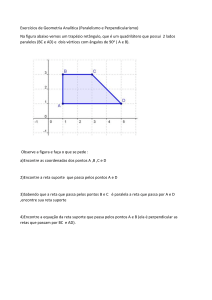
Enviado por
lalerick
Livro Matematica Geometria Euclidiana Espacial

Matemática Geometria Euclidiana Espacial Universidade Estadual do Ceará - Universidade Aberta do Brasil F iel a sua missão de interiorizar o ensino superior no estado Ceará, a UECE, como uma instituição que participa do Sistema Universidade Aberta do Brasil, vem ampliando a oferta de cursos de graduação e pós-graduação na modalidade de educação a distância, e gerando experiências e possibilidades inovadoras com uso das novas plataformas tecnológicas decorrentes da popularização da internet, funcionamento do cinturão digital e massificação dos computadores pessoais. Comprometida com a formação de professores em todos os níveis e a qualificação dos servidores públicos para bem servir ao Estado, os cursos da UAB/UECE atendem aos padrões de qualidade estabelecidos pelos normativos legais do Governo Federal e se articulam com as demandas de desenvolvimento das regiões do Ceará. Geometria Euclidiana Espacial Matemática Manoel Ferreira de Azevedo Filho Geografia 12 9 3 História Educação Física Química Ciências Biológicas Artes Plásticas Computação Física Matemática Pedagogia Matemática Geometria Euclidiana Espacial Manoel Ferreira de Azevedo Filho 3ª edição Fortaleza - Ceará Geografia 12 9 3 História 2015 Educação Física Química Ciências Biológicas Artes Plásticas Computação Física Matemática Pedagogia Copyright © 2015. Todos os direitos reservados desta edição à UAB/UECE. Nenhuma parte deste material poderá ser reproduzida, transmitida e gravada, por qualquer meio eletrônico, por fotocópia e outros, sem a prévia autorização, por escrito, dos autores. Editora Filiada à Presidenta da República Dilma Vana Rousseff Ministro da Educação Renato Janine Ribeiro Presidente da CAPES Carlos Afonso Nobre Diretor de Educação a Distância da CAPES Jean Marc Georges Mutzig Governador do Estado do Ceará Camilo Sobreira de Santana Reitor da Universidade Estadual do Ceará José Jackson Coelho Sampaio Vice-Reitor Hidelbrando dos Santos Soares Pró-Reitor de Pós-Graduação Jerffeson Teixeira de Souza Coordenador da SATE e UAB/UECE Francisco Fábio Castelo Branco Coordenadora Adjunta UAB/UECE Eloísa Maia Vidal Diretor do CCT/UECE Luciano Moura Cavalcante Coordenação da Licenciatura em Matemática Ana Carolina Costa Pereira Coordenação de Tutoria e Docência em Matemática Gerardo Oliveira Barbosa Editor da EdUECE Erasmo Miessa Ruiz Coordenadora Editorial Rocylânia Isidio de Oliveira Projeto Gráfico e Capa Roberto Santos Diagramador Francisco Oliveira Revisão Ortográfica Fernanda Ribeiro Conselho Editorial Antônio Luciano Pontes Eduardo Diatahy Bezerra de Menezes Emanuel Ângelo da Rocha Fragoso Francisco Horácio da Silva Frota Francisco Josênio Camelo Parente Gisafran Nazareno Mota Jucá José Ferreira Nunes Liduina Farias Almeida da Costa Lucili Grangeiro Cortez Luiz Cruz Lima Manfredo Ramos Marcelo Gurgel Carlos da Silva Marcony Silva Cunha Maria do Socorro Ferreira Osterne Maria Salete Bessa Jorge Silvia Maria Nóbrega-Therrien Conselho Consultivo Antônio Torres Montenegro (UFPE) Eliane P. Zamith Brito (FGV) Homero Santiago (USP) Ieda Maria Alves (USP) Manuel Domingos Neto (UFF) Maria do Socorro Silva Aragão (UFC) Maria Lírida Callou de Araújo e Mendonça (UNIFOR) Pierre Salama (Universidade de Paris VIII) Romeu Gomes (FIOCRUZ) Túlio Batista Franco (UFF) Dados Internacionais de Catalogação na Publicação Sistema de Bibliotecas Biblioteca Central Prof. Antônio Martins Filho Thelma Marylanda Silva de Melo Bibliotecária – CRB-3 / 623 A994g Azevedo Filho, Manoel Ferreira de Geometria euclidiana espacial / Manoel Ferreira de Azevedo Filho. 3. ed. – Fortaleza : EdUECE, 2015. 94 p. : il. ; 20,0cm x 25,5cm. (Matemática) ISBN: 978-85-7826-400-0 1. Geometria euclidiana espacial . I. Título. CDD: 512.5 Editora da Universidade Estadual do Ceará – EdUECE Av. Dr. Silas Munguba, 1700 – Campus do Itaperi – Reitoria – Fortaleza – Ceará CEP: 60714-903 – Fone: (85) 3101-9893 Internet: www.uece.br – E-mail: [email protected] Secretaria de Apoio às Tecnologias Educacionais Fone: (85) 3101-9962 Sumário Apresentação......................................................................................................5 Capítulo 1 – Paralelismo e Perpendicularismo.............................................7 Introdução...................................................................................................................9 1. Noções de Lógica................................................................................................10 1.1. Conjunção....................................................................................................10 1.2. Disjunção......................................................................................................10 1.3. Negação....................................................................................................... 11 1.4. Condicional................................................................................................... 11 1.5. Bicondicional................................................................................................ 11 2. Entes Primitivos e Axiomas da Geometria Euclidiana.......................................15 3. Paralelismo e Perpendicularismo........................................................................17 4. Ângulos.................................................................................................................24 Capítulo 2 – Cilindro, Cone e Esfera..............................................................33 1. Cilindro..................................................................................................................35 2. Cone......................................................................................................................39 3. Esfera....................................................................................................................44 Capítulo 3 – Volume e área de superfície.....................................................53 1. A Noção de Volume..............................................................................................56 2. Volume do Paralelepípedo Retangular...............................................................57 3. Volume do Cilindro, Cone e Esfera.....................................................................60 4. Área de Superfície................................................................................................64 Capítulo 4 – Poliedros......................................................................................73 1. Definições.............................................................................................................75 1.1 Representação Plana de um Poliedro Convexo........................................77 2. Relação de Euler..................................................................................................78 3. Poliedros Regulares.............................................................................................80 Sobre o autor.....................................................................................................94 Apresentação Este é um trabalho destinado a alunos que estão fazendo o curso de licenciatura ou bacharelado em Matemática, ou, àqueles que se interessam por geometria. O assunto aqui tratado, Geometria Euclidiana Espacial, é uma continuação natural da Geometria Eucilidiana Plana, a qual é, por conseguinte, pré-requisito para compreensão deste material. Procuramos um meio termo entre uma abordagem intuitiva e formal. Em alguns momentos somos formais, notadamente na Unidade 1, em outras, intuitivos. O trabalho está dividido em quatro unidades. Ao final de cada uma delas propomos exercícios que tentamos seqüenciá-los pela ordem crescente de dificuldade. Ao todo são 126. As respostas se encontram no final do trabalho. Outrossim, apresentamos ao longo do desenvolvimento do assunto, sempre que oportuno, algumas pequenas notas históricas relacionadas com o tema. O autor Capítulo Paralelismo e Perpendicularismo 1 Geometria Euclidiana Espacial 9 Objetivos • Conhecer os conceitos primitivos e definições básicas da Geometria Euclidiana Plana. • Vivenciar o contato com um tratamento axiomático de uma teoria matemática. • Conhecer e compreender os axiomas e os teoremas básicos sobre existência e unicidade acerca de paralelismo e perpendicularismo de retas e/ ou planos. • Saber definir ângulo entre planos e/ou retas no âmbito espacial. Introdução Diz a tradição que Tales de Mileto (624-548 a.C.) foi o precursor da geometria pela dedução. À ele atribui-se a autoria da demonstração, entre outros teoremas, de que "um ângulo inscrito num semi-círculo é um ângulo reto". Não existe documento que comprovem estas autorias. Outro matemático antigo, também precursor da geometria dedutiva, ao qual se lhe atribui a autoria da demonstração do famoso teorema – num triângulo retângulo o quadrado da hipotenusa é igual à soma dos quadrados dos catetos – é Pitágoras de Samos (580-500 a.C.). Devido à perda de documentos daquela época e pelo fato de que a escola fundada por ele era secreta, o teorema de Pitágoras assim como o da divisão áurea de um segmento, podem ter sido demonstrados por seus discípulos ou até mesmo pelos babilônios. Dois séculos depois, Euclides de Alexandria publicara o texto mais influente de todos os tempos: "Os Elementos" (300 a.C.). Os elementos de Euclides estão divididos em treze livros, dos quais somente os seis primeiros tratam de geometria plana elementar. Euclides organizou este assunto em 5 postulados, 5 “noções comuns” e mais de 150 proposições. As noções comuns são também princípios. A diferença destas para os postulados reside no fato de que as noções comuns são mais evidentes. Um tratamento moderno não faz esta distinção. Algumas críticas podem ser feitas à abordagem do assunto por Euclides. Por exemplo, os conceitos primitivos foram colocados como definições. Várias proposições foram demonstradas utilizando princípios não estabelecidos no texto tais como a unicidade da reta passando Depois da Bíblia, é o livro com mais edições publicadas (provavelmente mais de mil) 10 AZEVEDO FILHO, M. F. DE por dois pontos distintos dados. Contudo, por dois mil anos, Os Elementos constituiu o mais rigoroso tratado lógico dedutivo da matemática elementar. Neste trabalho, adotamos um tratamento intermediário entre intuitivo e formal. Não achamos adequado uma abordagem somente intuitiva. Por exemplo, o uso de figuras em geometria espacial, em certas situações, é impraticável para tirarmos conclusões. Em casos dessa natureza, nada melhor do que usar um raciocínio lógico-dedutivo. Utilizamos, nesta primeira unidade, uma abordagem axiomática (formal). O entendimento de um tratamento assim requer um mínimo de noções de lógica e o que significa esta abordagem. Por isso, iniciamo-lo com um parágrafo no qual damos estas noções. 1. Noções de Lógica Definição 1: Chama-se proposição toda oração afirmativa que pode ser classificada em um e somente um dos seguintes valores lógicos: verdadeira (V) ou falsa (F). Exemplo 2 Fortaleza é a capital do estado do Ceará. Exemplo 3 O Brasil possui, exatamente, 20 mil habitantes. Observemos que a conjunção de duas proposições só é verdadeira quando ambas são verdadeiras. Exemplo 4 3 + 2 = 5. Exemplo 5 Todo retângulo é um quadrado. As proposições são usualmente indicadas pelas letras p, q, r,... 1.1. Conjunção Definição 6: Dadas duas proposições p e q, definimos a conjunção de p e q e escrevemos p^q a proposição: p e q; ela é obtida intercalando-se o conectivo "e" entre as proposições p e q. Postulamos o valor lógico da conjunção p^q conforme a tabela de valores lógicos abaixo. p V V F F q V F V F p∧q V F F F 1.2. Disjunção Definição 7: A disjunção de duas proposições p e q denotada por p v q é definida intercalando-se o disjuntivo "ou" entre p e q; ei-la: p ou q. Geometria Euclidiana Espacial 11 Postulamos seu valor lógico de acordo com a tabela abaixo. p V V F F q V F V F p∨q V V V F 1.3. Negação Definição 8: Definimos a negação de uma proposição p e a indicamos por ~p como se segue: "É falso que p" ou, quando possível, colocando-se a palavra "não" antes do verbo da proposição p. Assim sendo, ~p diz precisamente o contrário de p. Postulamos seu valor lógico como sendo o oposto ao valor lógico de p. Confiramos a tabela abaixo. p V F ∼p F V 1.4. Condicional Definição 9: Outra proposição que se define a partir de duas proposições p e q dadas é a seguinte: (~p) v q. Indicamo-la por p q. Ela também pode ser lida de outros modos: se p então q; p é condição suficiente para q; q é condição necessária para p. Não postulamos e sim calculamos sua tabela de valores lógicos. Vejamos a seguir: p V V F F p q V F V F ∼p F F V V p →q V F V V Vale notarmos que p q só é falsa quando p é verdadeira e q é falsa. Se q é verdadeira, dizemos então que p implica q e podemos indicá-la por p q. Definição 10: Dada a proposição p a recíproca de p q. q, a proposição q p é chamada 1.5. Bicondicional Definitição 11: Podemos ainda, a partir de duas proposições p e q, definir a proposição p se e somente se q, denotada por p q, como sendo (p q)^(q p). Ela pode ser dita também da seguinte maneira: p é condição necessária e suficiente para q. Notemos que a disjunção de duas proposições só é falsa quando ambas são falsas. 12 AZEVEDO FILHO, M. F. DE Veja a seguir sua tabela de valores lógicos. p V V F F p →q V F V V q V F V F q →p V V F V p ↔q V F F V Observemos que p q é verdadeira quando as proposições p e q são ambas verdadeiras ou ambas falsas. Neste caso, dizemos que p é equivalente a q e podemos denotá-la por p q. Por conseguinte, duas proposições são equivalentes quando e apenas quando elas possuem o mesmo valor lógico. Abaixo mostramos exemplos de proposições equivalentes. Exemplo 12 ~(p v q) p V V F F q V F V F Exemplo 13 ~(p ^ q) p V V F F Exemplo 14 ~(p Podemos formar mais proposições a partir de outras conbinações das conjunções, disjuntivos, negações, condicionais, etc. (~p)^(~q) ∼p F F V V ∼q F V F V p ∨q V V V F ∼(p ∨q) F F F V (∼p) ∧(∼q) F F F V p∧q V F F F ∼(p ∧ q) F V V V (∼p) ∨(∼q) F V V V (~p) v (~q) q V F V F ∼p F F V V q) p^(~q) p V V F F q V F V F ∼q F V F V ∼q F V F V p→q V F V V ∼(p →q) p ∧(∼q) F F V V F F F F Os exemplos 5, 6 e 7 nos fornecem substitutos para a negação, respectivamente, da disjunção, conjunção e do condicional de duas proposições. Notemos, por exemplo, que para ~(p q) ser verdadeira, é necessário e suficiente que p e ~q, simultaneamente, sejam verdadeiras; assim como para que ~(p^q) seja verdadeira, basta que pelo menos uma das proposições ~p ou ~q seja verdadeira, isto é, p ou q seja falsa. Vejamos mais exemplos. Geometria Euclidiana Espacial 13 Exemplo 15 (p q) ( (~q) p V V F F q V F V F (~p) ) ∼q F V F V ∼p F F V V p →q V F V V Exemplo 16 Sendo f falsa, temos: (p p V V F F q V F V F Exemplo 17 ~(~p) ( ( (~q)^p) (∼q) ∧p F V F F p→q V F V V f) ((∼q) ∧p) → f V F V V p Exemplo 18 (p v q) (q v p) Exemplo 19 (p q) ( (p Exemplo 20 (p v q) ( (~p) Exemplo 21 ( (p ∼q F V F V f F F F F q) (∼q) →(∼p) V F V V q)^(q q)^( (~p) r) ) (~q) ) ) q) (p r) Na organização de um tratamento formal de uma teoria matemática, como é o caso desta unidade, existem os chamados conceitos primitivos. Eles não são definíveis e apenas são perceptíveis. A partir deles é que definimos os demais conceitos. Eles são os pontos de partida da teoria. A razão de suas existências reside no seguinte argumento: para se definir um certo conceito, utilizamos outros já estabelecidos. Para definir estes, precisamos de outros e assim por diante. Sendo finita a quantidade de conceitos, decorre que esbarraremos naqueles não expressos a partir de outros. São esses os conceitos primitivos. Por exemplo, na geometria, para se definir triângulo, utiliza-se entre outros o conceito de segmento de reta. Para definir este, necessita-se do conceito de reta que é primitivo. Além dos conceitos primitivos, há os chamados princípios, também denominados de postulados ou axiomas. Os princípios são propriedades envolvendo os conceitos primitivos ou outros já estabelecidos, ou, simplesmente, propriedades, não carentes de demonstração. Eles geralmente são bem aceitáveis, embora isto não seja uma condição necessária. Exemplo de um axioma: por dois pontos distintos passa uma única reta. Esse postulado fornece uma propriedade relacionando dois entes primitivos da geometria: ponto e reta. A verificação destas últimas afirmações deixadas a seu cargo. 14 AZEVEDO FILHO, M. F. DE Os resultados aos quais chega uma teoria depende dos princípios que são estabelecidos. Por exemplo, na geometria euclidiana plana chega-se à conclusão de que a soma dos ângulos internos de um triângulo é igual a 180o. Já na geometria de Lobatchewski - Bolyai conclui-se que esta soma é menor do que 180o. A razão dessa divergência de resultados reside na diferença dos axiomas em que se basearam as teorias. Também fazem parte do desenvolvimento formal de uma teoria matemática as proposições (no sentido que definimos no início deste parágrafo), as quais são carentes de uma prova (demonstração) que se baseia nos princípios ou em outras proposições já provadas. Em geral, elas são do tipo p q. A proposição p é chamada de hipótese e a q de tese. Como provar uma proposição do tipo p q? Vejamos. Se p é falsa, então p q é sempre verdadeira indepentemente de q ser verdadeira ou falsa de acordo com a tabela de valores lógicos. Se p é verdadeira, para que p q seja verdadeira é necessário e suficiente que q seja verdadeira. Por conseguinte, demonstrar uma proposição do tipo p q , consiste em admitir p verdadeira e a partir daí concluir que q é verdadeira. Às vezes, é mais conveniente, para provar a proposição p q, usar o seguinte argumento, baseado na equivalência do exemplo 16: negando a tese e admitindo a hipótese, a proposição fica demonstrada se isto acarretar em uma proposição falsa (contradição). A idéia é que se chegamos a uma contradição, então a negação da tese não pode ser verdadeira e portanto a tese é verdadeira. Este argumento chama-se demonstração indireta ou demonstração por absurdo. Podemos também utilizar a equivalência do exemplo 16 para demonstrar uma proposição do tipo p q. Chamamos ainda a atenção para o exemplo 20 que nos fornece um argumento para demonstrar proposições do tipo p v q. Vejamos que para esta ser verdadeira basta a negação de p implicar em q. Apresentaremos agora terminologias para certas proposições. Chama-se teorema toda proposição de grande relevância; lema é uma proposição que será utilizada na demonstração de outra ou de um teorema; corolário é a denominação de toda proposição que é consequência imediata de outra ou de um teorema; escólio é qualquer proposição extraída da demonstração de outra. Um dos entes primitivos da matemática é o conceito de conjunto ou coleção. Entendemos por conjunto toda coleção de objetos bem definidos. Exemplos: o conjunto dos seres humanos que moram no Brasil; o conjunto formado pelos alunos de uma dada universidade; o conjunto dos grãos de areia existentes no nosso planeta; conjunto constituído de conjuntos; etc. Cada objeto da coleção, que também é um conceito primitivo, é chamado de Geometria Euclidiana Espacial 15 elemento do conjunto. Se o elemento é membro do conjunto A, dizemos que pertence a A e escrevemos para indicar esse fato. Chama-se sentença aberta toda proposição p(x) aplicável aos elementos x de um conjunto A dado explícito ou implicitamente. Exemplo: x é um homem alto. Nesse exemplo, o conjunto que contém o elemento x está implícito. Vale ressaltar que a relação de pertinência é também um conceito primitivo. Podemos inserir às sentenças abertas os chamados quantificadores: universal indicado por ou existencial denotado por . O símbolo significa ``para todo’’ ou ``para qualquer que seja’’ ou ainda ``para cada’’ enquanto que indica ``existe um’’ ou ``existe pelo menos um’’ ou ainda ``para algum’’. x tal que p(x)’’ são Se p(x) é uma sentença aberta, então " x, p(x)" ou proposições quantificadas. Vale salientarmos que a negação de " x, p(x)" é " x tal que ~ p(x)’’ enquanto que a negação de " x tal que p(x)’’ é " x, ~p(x)" Por exemplo, a negação de ``todo homem é alto’’ é ``existe um homem que não é alto’’. 2. Entes Primitivos e Axiomas da Geometria Euclidiana Axioma 1. Existem um conjunto, denominado espaço, e duas coleções de subconjuntos do espaço satisfazendo às propriedades enunciadas nos axiomas subseqüentes. Os elementos do espaço são chamados de pontos, os de uma das coleções referidas no axioma 1 são denominados retas e os da outra, planos. Ponto, reta e plano são os conceitos primitivos da geometria euclidiana plana. Os pontos são denotados usualmente por letras maiúsculas A, B, C,...; as Intuiretas por letras minúsculas r, s, t,...; e os planos por letras gregas tivamente, podemos imaginar que uma ``porção’’ de um plano é a superfície de uma mesa ou uma folha de papel estirada; uma ``porção’’ de uma reta é um risco feito nesta folha com o auxílio de uma régua, ou, um cordão esticado; e um ponto é um furinho feito com a ponta de um alfinete numa folha ou um pingo feito com uma caneta, etc. O espaço pode ser pensado como sendo nosso ambiente. Diremos que dois ou mais pontos são coplanares ou colineares, respectivamente, se pertencem a um mesmo plano ou a uma mesma reta; diremos ainda que dois ou mais conjuntos não vazios de pontos são coplanares ou colineares se todos os seus pontos são, respectivamente, coplanares ou colineares. Se um ponto A pertence a uma reta r ou a um plano é usual dizer que r ou passa por A. Estabelecida essa linguagem inicial, fixaremos a seguir alguns princípios. Axioma 2. Por dois pontos distintos passa uma única reta. Se A e B são pontos distintos pertencentes à reta r, denotamos ou Vale observar que os elementos das retas e dos planos são pontos. 16 AZEVEDO FILHO, M. F. DE Estabeleceremos a seguir resultados decorrentes destes axionas. Axioma 3. Por três pontos não colineares passa um único plano. Axioma 4. Se o plano passa por dois pontos distintos A e B, então Axioma 5. Se a interseção de dois planos é não vazia, então esta contém pelo menos dois pontos distintos. Axioma 6. Cada reta contém pelo menos dois pontos distintos; todo plano contém no mínimo três pontos não colineares; o espaço contém pelo menos quatro pontos distintos entre si não coplanares e não colineares. Como conseqüência do axioma 2, podemos concluir que a interseção de duas retas distintas é um conjunto unitário ou o conjunto vazio. No primeiro caso, dizemos que elas são concorrentes e no segundo dizemos que são reversas se não são coplanares, e, paralelas (e distintas) se são. Usaremos a notação r//s para indicar que uma reta r é paralela a uma reta s. Passemos agora a analisar as possibilidades acerca da interseção de . Ela poder ser ou não vazia. No caso de ser vazia, dois planos distintos . Se dizemos que os planos são paralelos (e distintos) e escrevemos não, o axioma 5 garante que esta interseção contém pelo menos dois pontos e distintos A e B. Pelo axioma 4, podemos concluir que Na realidade, De fato, de acordo com o axiodonde, (isto é, nenhum ponto não pertencente a ma 3, nenhum ponto fora da reta ) pode pertencer a uma vez que Em resumo, a interseção de dois planos distintos é vazia ou é uma reta. No caso de ser uma reta, diremos que os planos são concorrentes. O que pode ser a interseção de uma reta com um plano? Respondamos. Se ela contém dois pontos, então, pelo axioma 4, a reta está contida no plano, donde, a interseção é a própria reta. Restam as seguintes possibilidades: vazia ou conjunto unitário. Na primeira dizemos que a reta e o plano são paralelos e na segunda dizemos que a reta fura o plano ou ela para indicar que uma reta r é é secante à ele. Adotaremos a notação paralela a um plano . Existe um único plano contendo uma reta e um ponto fora desta, dados, assim como há um único plano contendo duas retas concorrentes dadas. Justifiquemos a primeira afirmação. Pelo axioma 6, existem dois pontos distintos A e B pertencentes à reta dada. Seja C o ponto fora desta. Assim sendo, A, B e C não são colineares. Pelo axioma 3, existe um único plano que contém A, B e C. Este também contém a reta, graças ao axioma 4. A unicidade seguee C contém A, B e C. Provemos agora -se porque todo plano que contém Sejam a segunda assertiva. Sejam r e s as retas concorrentes e usando o axioma 6. Temos aí três pontos não colineares: A, B e C. O plano determinado por A, B e C contém r e s. Qualquer que seja o plano contendo r e s, contém A, B e C e, por conseguinte, é igual a . Geometria Euclidiana Espacial 17 Também, dadas duas retas paralelas existe um único plano que as contém. Axioma 7. (Postulado de Euclides) Por um ponto fora de uma reta passa uma única reta paralela à reta dada. Levou-se a crer que o postulado de Euclides, o quinto de seu trabalho, pudesse ser demonstrado a partir dos quatro outros. De modo que matemáticos famosos, que passaram-se em quase dois mil anos, o tentaram. Somente no século XIX é que dois matemáticos, trabalhando independentemente, provaram a independência do quinto postulado. Foram eles, Nicolai Lobachevsky (1793 - 1856), russo, e o húngaro Johan Bolyai (1802 - 1860). Foi com o artigo “On the Principles of Geometry “ em 1829 publicado por Lobachevsky, que ficou provado definitivamente que o quinto postulado não podia ser obtido a partir dos demais. A prova consistiu em substituí-lo por outro que lhe é contraditório e a partir disto demonstrou-se que a soma dos ângulos internos de um triângulo é menor do que 180o, resultado este que entra em choque com o teorema da geometria euclidiana plana que afirma ser igual a 180o esta soma. 3. Paralelismo e Perpendicularismo Doravante, admitiremos todos os resultados concernentes à geometria euclidiana plana. Passemos aos teoremas básicos acerca de paralelismo e perpendicularismo de retas ou planos que são assuntos sob os cuidados da geometria euclidiana espacial. Teorema 22 Sejam r uma reta paralela a um plano a reta paralela a r passando por P está contida em Prova. Seja correntes. Seja o plano determinado por P e r. Temos que A chamada geometrica não-euclidiana nascia oficialmente com aquele artigo. . Então, são con- Pelo fato de e r ser paralela a , segue-se que e pelo fato de s e r serem coplanares (estão contidas em ), vem que s e r são para, decorre que . Assim sendo, a reta lelas. Desde que P é comum a paralela a r passando por P está contida em . Teorema 23 Se uma reta r é paralela a um plano , então existe uma reta contida em paralela a r (e distinta). Prova. Seja P um ponto qualquer de . Pelo Teorema 22, a reta paralela a r passando por P está contida em . Logo, segue-se o resultado. Deixamos a prova deste fato como exercício. 18 AZEVEDO FILHO, M. F. DE Teorema 24 Se uma reta r é paralela a uma reta r' contida num plano e não está contida nesse plano, então r é paralela a Prova. Por absurdo, suponhamos que r fura . Seja Seja o plano determinado por r e r'. Temos: . Sendo e . Como , segue-se que . Isto é uma convem que e r ser paralela (e distinta) a r'. tradição ao fato de Teorema 25 Sejam r e s, e, u e v pares de retas concorrentes. Se r//u e s//v, então os planos determinados por r e s, e, u e v são paralelos ou coincidentes. Esse teorema corresponde ao quinto postulado de Euclides na versão de plano. Prova. Sejam o plano determinado por r e s e o plano determina. Devemos mostrar que . Antes, do por u e v. Suponhamos que . mostraremos que r não está contida em . Por absurdo, suponha que , pois do contrário, como s é Assim sendo, teremos necessariamente ,o paralela a uma reta contida em , pelo Teorema 24, decorreria que . que seria uma contradição ao fato de um ponto de s pertencer a r e e , então . Contradição! Portanto, Posto que , já que r é paralela Isto implica, de acordo com o Teorema 24, que . Dado que s tem um ponto em comum com r e a uma reta contida em , segue-se que e daí, pelo Teorema 24, , uma vez que s é paralela a uma reta contida em Enfim, r e s são retas paralelas a Para encerrar a demonstração, suponhamos, por absurdo, que e . Então, t, r e s são conão são paralelos. Como são distintos, seja planares. Como r e s são concorrentes, t não é simultaneamentre paralela a r e s. Assim, t é concorrente a uma delas, já que t é distinta de ambas. Digamos, . Isto é uma contradição ao fato de . r. Seja Teorema 26 Por um ponto não pertencente a um plano, passa um único plano paralelo ao plano dado. Prova. (Existência)Sejam P um ponto e um plano tais que . Sejam u e v retas concorrentes contidas em e r e s as retas passando por P, respectivamente, paralelas a u e v. É óbvio que r e s não estão contidas no plano . Pelo teorema anterior, o plano determinado por r e s é paralelo a . (Unicidade) Seja um plano paralelo a passando por P. Mostraremos . É claro que as retas concorrentes u e v contidas em são paralelas que Geometria Euclidiana Espacial 19 ao plano Pelo Teorema 22, as respectivas paralelas a u e v passando por P . Essas paralelas são r e s. Posto que estão contidas em , uma vez que . duas retas concorrentes determinam um único plano, segue-se que Teorema 27 Se uma reta fura um plano, fura também qualquer plano paralelo a esse plano. planos paralelos e r uma reta que fura o plano Prova. Sejam e num ponto P. Por absurdo, suponhamos que r não fura o plano . Como , então , logo, . Seja tal que . Desse modo, tee , e r a paralela a s passando por P. Pelo mos: . Contradição! Teorema 22, segue-se que Teorema 28 Se então . . Do contrário, teríProva. Inicialmente, vamos mostrar que amos duas retas distintas, s e t, paralelas a r passando por um mesmo ponto fora de r. Isto iria contradizer o axioma das paralelas (axioma 7). Logo, . Resta provarmos que s e t são coplanares. Sejam e . e o plano determinado por u e s. Distinguiremos dois casos: Sejam Caso 1. . O plano contendo t e r tem um ponto em comum com , o . Desde que uma reta e um ponto fora desta deponto B, e a reta r, em que terminam um único plano, segue-se que = e, portanto, s e t são coplanares. Caso 2. Sendo , pelo Teorema 24, decorre que . Assim sendo, pelo está contida em Essa Teorema 22, a reta paralela a r passando por reta é t. Por conseguinte, t e s estão contidas em . Teorema 29 Sejam r e s, e, u e v pares de retas concorrentes. Se r//u e s//v, então Prova. Sejam . Se os planos que contêm r e s, e, u e v são iguais, o resultado é fácil de demonstrar. Deixamos a prova detalhada do teorema para este caso como exercício. Suponhamos que os planos são distintos. Seja o plano que contém r e u, e, o que contém s e v. Se considerássemos a coincidência de retas como sendo paralelismo, este seria o teorema que garantiria a transitividade da relação de paralelismo entre retas 20 AZEVEDO FILHO, M. F. DE Temos .Sejam mesmo semi-plano determinado por e em pontos pertencentes a um tais que . Desse modo, ABQP é um paralelogramo, donde, . Sejam C s e D v ponem tais que tos pertencentes a um mesmo semi-plano determinado por . Assim sendo, CDQP é um paralelogramo, donde, . Dessa . maneira, temos, pela transitividade do paralelismo entre retas, que Dado que r//u e s//v, vem, conforme o Teorema 25, que os planos determinados . Posto que por r e s, e, u e v são paralelos, logo, . Assim sendo, ABDC é um paralelosão coplanares, segue-se que . Logo, (L.L.L.) e, por conseguinte, gramo, donde, . Portanto, . Definição 30 Diremos que uma reta r que fura um plano num ponto O é perpendicular a em O ou, simplesmente, perpendicular a se toda reta contida em passando por O é perpendicular a r. Nesse caso, diremos ainda que O é o pé da perpendicular r em Teorema 31 Seja o plano determinado por duas retas concorrentes r e s no ponto O. Se uma reta t é perpendicular a r e a s em O, então t é perpendicular a em O. Prova. Seja u uma reta qualquer contida em passando por O. Mos. Podemos supor, sem perda de generalidade, que u ≠r traremos que e u ≠s. Tomemos em r e s, respectivamente, pontos A e B tais que A e B se encontram em semi-planos abertos opostos em relação a u. Geometria Euclidiana Espacial 21 O segmento intercepta u num ponto C entre A e B. Sejam D e D' . Sendo t perpendicular pontos distintos em t tais que O é ponto médio de a r, segue-se, pelo caso L.A.L. de congruência de triângulos, que AOD AOD' BOD'. Desse e sendo t perpendicular a s, decorre, por L.A.L., que BOD ABD' e, portanto, BÂD modo, AD = AD' e BD = BD', donde, por L.L.L., ABD BÂD'. Isto acarreta, por L.A.L., que CAD CAD', por conseguinte, CD = COD'. Este fato implicará que CÔD é CD'. Assim sendo, por L.L.L., COD . reto e, portanto, Teorema 32 Seja P um ponto pertencente a um plano . Então, existe uma única reta r passando por P perpendicular a , em que A ≠ P, , e o plano Prova. (Existência) Sejam e B. Sejam a reta perpendicular a passando determinado por a reta perpendicular a passando por P. por P e Temos que u e v são retas concorrentes em P. Seja o plano detera reta perpendicular a v passando por P. Nessa minado por u e v e , logo, é perpendicular a construção, observemos que Agora, qualquer reta contida em passando por P. Em particular, notemos que r é perpendicular a duas retas concorrentes contidas em , a 22 AZEVEDO FILHO, M. F. DE saber: e v. Por conseguinte, r é perpendicular a e passa por P. (Unicidade) Seja s uma reta perpendicular a passando por P. Mostraremos que r = s. Por absurdo, suponhamos que r ≠ s. Assim, r e s concorrem é conao ponto P em . Seja o plano determinado por r e s. Temos que . Desse modo, r, s e t são coplanares (estão em corrente a . Seja ), em que r e s são perpendiculares a t no ponto P. Contradição! Teorema 33 Sejam r e s retas distintas, em que r é perpendicular a . Então, Prova. ( ) Seja o plano determinado por r e s. Como r fura , então é concorrente a . Seja . Assim, r, s e t são coplanares (estão . contidas em ), sendo que . Sejam . Sejam u e v em , Como r//s, então respectivamente, perpendiculares a t em A e B. Desse modo, u//v e como r//s, segue-se que , de acor, então . Enfim, s do com o Teorema 29. Desde que, por hipótese, é perpendicular a duas retas concorrentes contidas em , a saber: t e v. Por . conseguinte, ( ) Sejam A e B, respectivamente, os pés das perpendiculares r e s em . Seja s' a reta paralela a r passando por B. Pela implicação ( ) deste teorema, segue-se que s' é perpendicular a . Sendo s e s' pependiculares a decorre, pela unicidade do Teorema 32, que s = s'. Logo, passando por s é paralela a r. Teorema 34 Por um ponto fora de um plano, passa uma única reta perpendicular a esse plano. um ponto. Seja o plano Prova. (Existência) Sejam um plano e paralelo a passando por P. Seja r a reta perpendicular a passando por P. Geometria Euclidiana Espacial 23 Como , então r fura também , digamos, num ponto Q. Seja uma reta qualquer passando por Q. Vamos mostrar que . Seja , vem, pelo Teorema 22, v a reta paralela a u passando por P. Sendo . Desde que , segue-se que . Posto que r é transverque . Conclusão: r é perpendicular a sal às paralelas u e v, decorre que e passa por P. (Unicidade) Seja r' uma reta perpendicular a passando por P. De. Seja Q' vemos mostrar que r' = r. Para isso, basta mostrarmos que o pé da perpendicular r' em Mostraremos que Q' = Q. Por absurdo, suponhamos que Q' ≠ Q. Assim, a soma dos ângulos internos do triângulo PQQ' e, portanto, é maior do que 180o. Contradição! Logo, Q' = Q, donde, r' = r. ESCÓLIO. Se uma reta é perpendicular a um plano , então é perpendicular a qualquer plano paralelo a Definição 35 Sejam um plano e um ponto. Definimos a distância de P a , denotada por d(P, ), como sendo a distância de P ao pé da a distância de P a é definida perpendicular a passando por P. Se como sendo zero. Definição 36 Sejam e dois planos paralelos. Definimos a distância entre e , denotada por d( , ), como sendo a distância de um ponto qualquer de um dos dois planos ao outro plano. Teorema 37 Sejam r e s retas reversas. Então, existem dois únicos planos paralelos (e distintos) e tais que Prova. (Existência) Seja um ponto qualquer e s'//s passando por um ponto qualquer e r'//r passando por B. A. Seja Observe que a distancia de P a nos dois casos, é a menor das distâncias de P aos pontos de . A título de exercício, demostre que essa definição, de fato, não depende do ponto e nem do plano escolhidos. 24 AZEVEDO FILHO, M. F. DE Como r e s são reversas, então r e s' e r' e s são pares de retas concorrentes. Sejam o plano determinado por r e s' e o determinado por r' e s. A reta r não está contida em , pois r e s são reversas, conseqüentemente, ≠ . Pelo Teorema 25, segue-se que e são paralelos. (Unicidade) Sejam ' e planos paralelos tais que Devemos mostrar que ' = e ' = . Temos: r é paralela a ', pois ' e '// '. Pelo Teorema 22, segue-se que a reta paralela a r passando está contida em '. Esta reta é r'. Assim, ' é o plano determinado por B pelas retas concorrentes r' e s. Portanto, ' = . Posto que e ' são planos paralelos a e passam pelo ponto A (pois contêm a reta r), decorre que ' = , de acordo com o Teorema 26. Definição 38 Definimos a distância entre duas retas reversas como sendo a distância entre os planos paralelos referidos no teorema anterior. 4. Ângulos Vejamos como se define o ângulo entre elas. Sejam r e s retas. Já é conhecida a definição do ângulo entre r e s caso elas sejam coplanares. Vamos rever. Se elas são coincidentes ou paralelas dizemos que o ângulo entre elas é zero. Se são concorrentes, elas formam dois pares de ângulos opostos pelo vértice (que têm mesma medida) sendo que dois desses ângulos não opostos pelo vértice são suplementares. Neste caso, o ângulo entre elas é, por definição, o menor dos quatro ângulos. A novidade ocorre quando as retas r e s são reversas. pontos quaisquer, r' a reta paralela Definição 39 Sejam a r passando por B e s' a reta paralela a s passando por A. Pelo Teorema 29, . Este será, por definição, o ângulo entre as retas r e s (o qual independe da escolha dos pontos A e B). Definição 40 Diremos que duas retas são ortogonais se o ângulo entre elas é de 90o. Vamos agora definir ângulo entre dois planos. Definição 41 Se dois planos são coincidentes ou paralelos dizemos que o ângulo entre eles é zero. Suponhamos que dois planos e são con. Sejam A, B t, distintos, r e r' as perpendiculares a correntes. Seja t em passando, respectivamente, por A e B, e, s e s' as perpendiculares a t em passando, respectivamente, por A e B. Geometria Euclidiana Espacial 25 Assim, temos r e s, e, r' e s' pares de retas concorrentes tais que r//r' e . Este será, por definição, o ângulo s//s'. Pelo Teorema 29, entre os planos e (o qual independe da escolha dos pontos A e B). Definição 42 Diremos que dois planos são perpendiculares se o ângulo entre eles mede 90o. Definição 43 Chama-se diedro ou ângulo diedral a reunião de dois semi-planos com mesma origem. Os semi-planos são chamados de faces do diedro e a origem comum chama-se aresta. Definição 44 Se as faces de um ângulo diedral são semi-planos coincidentes ou opostos a medida do ângulo diedral é, por definição, respectivamente, zero ou 180o. Suponhamos que os planos que contêm as faces são concorrentes. Sejam A e B dois pontos distintos pertencentes à aresta. A partir de A traperpendiculares à aresta, uma em cada face cemos as semi-retas também perpendiculares à e a partir de B tracemos as semi-retas contida na mesma face em que se encontra aresta, sendo tais que BC = AD e BF = AE. contida na mesma face em que se encontra Iremos agora definir a medida de um ângulo diedral. 26 AZEVEDO FILHO, M. F. DE Desse modo, ABCD e ABFE são paralelogramos, o que implica que CDEF (L.L.L.). Assim sendo, é também um paralelogramo, donde, . Definiremos a medida do ângulo diedral, nesse caso, como sendo a medida de DÂE que independe do ponto escolhido sobre a aresta. Definição 45 Todo plano reparte o espaço em três subconjuntos: o próprio plano, o subconjunto dos pontos que ficam a um mesmo lado do plano e o subconjunto dos pontos que ficam no outro lado. Cada um desses dois ea últimos subconjuntos chama-se semi-espaço aberto determinado por união do plano com um semi-espaço aberto chama-se semi-espaço fechado determinado por ou, simplesmente, semi-espaço. Assim, um plano determina dois semi-espaços que chamaremos de semi-espaços opostos em relação a . Dados dois pontos A e B distintos e não pertencentes a , então A e B se situam num mesmo semi-espaço determinado por Interseção de conjuntos convexos é um conjunto convexo. Definição 46 Um conjunto S, subconjunto do espaço, chama-se conveS. xo se goza da seguinte propriedade: dados A, B S, distintos, então Todo semi-espaço é um conjunto convexo. Considere um ângulo diedral de aresta r e cujas faces e não são coplanares. Sejam E e F, respectivamente, o semi-espaço determicontendo e o semi-espaço determinado por contendo . nado por E F é um conjunto convexo por ser interseção de dois conjuntos convexos, o qual será chamado de região convexa determinada pelo diedro. Geometria Euclidiana Espacial 27 Definição 47 (Bissetor de um diedro) Chama-se bissetor de um ângulo diedral de aresta r e cujas faces e não são coplanares o semi-plano de origem r, contido na região convexa determinada pelo diedro, que o divide em dois ângulos diedrais com mesma medida. Precisamos mostrar que todo diedro, cujas faces não são coplanares, tem um único bissetor. É o que faremos agora. Sejam r a aresta e e as e faces de um tal ângulo diedral. Seja A r um ponto qualquer, , perpendiculares a r. Seja a bissetriz do ângulo BÂC. Desde que , então r é perpendicular ao plano determinado por A, B . Seja o plano determinado por r e . Assim, o semie C, logo, é bissetor do diedro. -plano contido em determinado por r contendo A unicidade segue-se da unicidade da bissetriz de um ângulo BÂC. Definição 48 Chama-se triedro a reunião de três ângulos não rasos, com mesmo vértice, contidos em planos distintos, tais que a interseção de dois quaisquer é um lado comum. O vértice comum aos três ângulos chama-se vértice do triedro; cada lado comum denomina-se aresta e cada ângulo chama-se face. Um triedro é denominado tri-retângulo se os planos que contêm as faces são mutuamente perpendiculares. Teorema 49 Sejam r uma reta que fura um plano num ponto P, A r - {P} e A' o pé da perpendicular a passando em A. Então, r é perpendicular A' = P. a Prova. ( ) Temos: r e são perpendiculares a e passam no ponto Os detalhes da demonstração deixamos a seu cargo. 28 AZEVEDO FILHO, M. F. DE . Pela unicidade do Teorema 34, segue-se que e r fura , decorre que A' = P. ( ) Temos: . Sendo . Desde que , segue-se que . Definição 50 Dados um ponto A e um plano , o pé da perpendicular a passando por A chama-se projeção ortogonal de A em ou, simplesmente, projeção de A em . Teorema 51 Seja r uma reta não perpendicular a um plano . Sejam A, B, C r, distintos, e A', B' e C' as projeções, respectivamente, de A, B e C em . Então, A', B' e C' são distintos e colineares. Prova. Podemos supor que . Assim, dois dentre os pontos A, B e C não pertencem a . Digamos, A e B. Se A' = B', pela unicidade do Teo. Assim sendo, rema 32, decorre que e, portanto, r é perpendicular a , o que é uma contradição. Logo, A'≠B'. Note e, por conseguinte, pelo Teorema 33, . Seja o que . Temos que e são concorrentes, pois plano determinado por e . Mais precisamente, . Quanto a C, ou C . Se C , então C = C' e, pelo há duas possibilidades: C Teorema 49, C' ≠ A' e C' ≠ B', já que r não é perpendicular a . Desde que (pois ), segue-se que C', A' e B' são colineares. Se C , temos, em particular, que A e C não pertencem a . Usando o mesmo raciocínio empregado no início dessa demonstração, chegaremos que e a interseção do plano determinado por . Entretanto, os planos e têm em comum a reta r e o com o plano é , logo, são iguais, donde, e, por ponto conseguinte, A', B' e C' são colineares. Para encerrar, temos também que C' ≠ B' pois do contrário r seria perpendicular a . Observe que a Projeção de A em só é igual a A se A . Seja r uma reta não perpendicular a um plano . Sejam A, B r, distintos, . e A' e B' as projeções de A e B em . Pelo Teorema 51, A' ≠ B'. Seja Seja C r um ponto qualquer. Pelo Teorema 51, podemos concluir que a projeção de C em , C', pertence a r'. Em outras palavras, as projeções dos pontos de r em são colineares. A reta r' chama-se a projeção ortogonal de r em ou, simplesmente, a projeção de r em Se r é perpendicular a , então todos os pontos de r, conforme o Teorema 49, se projetam no pé da perpendicular de r em . Neste caso, diremos que o pé da perpendicular de r em é a projeção de r em . Geometria Euclidiana Espacial 29 Definição 52 Definimos o ângulo entre uma reta r e um plano como sendo 90o se r é perpendicular a e se r não é perpendicular a como sendo o ângulo que r faz com sua projeção sobre . Síntese do Capítulo No início, estabelecemos noções rudimentares de Lógica Matemática. Em seguida, apresentamos os primeiros axiomas da Geometria Euclidiana Espacial e suas conseqüências básicas. Vimos vários teoremas que envolvem propriedades do paralelismo e perpendicularismo relativos a planos e/ou retas no espaço. Demos definições e resultados concernentes a ângulos de um modo geral tais como ângulo diedral. Ao final, estudamos projeção ortogonal de retas em planos. Atividades de avaliação 1. Prove as afirmações abaixo: a) O espaço contém, pelo menos, seis retas e quatro planos. b) Por um ponto passam, no mínimo, três retas. c) Três pontos não colineares são distintos entre si. d) Dada uma reta, há, pelo menos, dois planos que a contêm. e) Um plano contém pelo menos três retas. f) Dados um plano e um ponto pertencente a , existem, no mínimo, duas retas contidas em passando por esse ponto. 2. Seja F uma figura tal que quatro quaisquer de seus pontos sejam coplanares. Mostre que F é plana, isto é, está contida num plano. 3. Explique por que uma mesa com três pernas sempre fica firme sobre um piso plano e uma de quatro pernas pode ficar em falso. 4. Uma figura é formada por quatro pontos A, B, C e D e pelos segmentos . Ela é uma figura plana? 5. Três planos distintos têm em comum dois pontos. Mostre que existe uma reta comum aos três planos. 6. Seja t uma reta contida em dois planos distintos. Mostre que t é a interseção desses dois planos. 7. Dois triângulos ABC e DEF, situados em dois planos distintos, são tais que 30 AZEVEDO FILHO, M. F. DE as retas encontram as retas e nos pontos M, N e P, respectivamente. Mostre que M, N e P são colineares. 8. Sejam s uma reta e um plano tais que s|| . Demonstre que existe um único plano paralelo a (e distinto) contendo s. 9. Mostre que se uma reta é paralela a dois planos concorrentes, então ela é paralela à reta de interseção dos dois planos. 10. Suponha que três planos têm exatamente um ponto em comum. Mostre que não existe nenhuma reta simultaneamente paralela a . 11. Seja r uma reta secante a um plano e P um ponto exterior a . Mostre que existe uma única reta que passa por P, encontra r e é paralela a 12. Mostre que se um plano é concorrente a um plano , é também concorrente a qualquer plano paralelo a . 13. Use o exercício anterior para concluir que se dois planos paralelos são cortados por dois planos paralelos, concorrentes aos anteriores, então as interseções serão quatro retas paralelas. 14. Considere duas retas paralelas secantes a dois planos paralelos. Mostre que os segmentos destas retas determinados pelos dois planos são congruentes. 15. Pode existir uma reta paralela a duas retas reversas? 16. Mostre que se duas retas são reversas, então todo plano determinado por uma e um ponto da outra é secante a esta. 17. Mostre que se uma reta fura um plano num ponto não pertencente a uma reta contida nesse plano, então estas retas são reversas. 18. Sejam r e s duas retas reversas. Sejam A e B pontos distintos de r e C e D são reversas. pontos distintos de s. Mostre que as retas 19. Sejam r e s duas retas reversas, A um ponto em r e B um ponto em s. Qual é a interseção do plano definido por r e B com o plano definido por s e A? 20. Mostre que por um ponto dado se pode traçar uma única reta ortogonal a duas retas não paralelas dadas. 21. Sejam A, B e C pontos não colineares. Mostre que se as retas também é ortogonal a r. são ortogonais à reta r, então e 22. Considere um conjunto com pelo menos três retas distintas. Mostre que se duas quaisquer dessas retas são concorrentes, então elas estão todas num mesmo plano ou passam todas num mesmo ponto. 23. Mostre que dois ângulos diedrais opostos pela aresta têm a mesma medida. 24. Mostre que o ângulo formado entre um plano e um plano ângulo formado por e qualquer plano paralelo a . é igual ao Geometria Euclidiana Espacial 31 25. Uma reta r faz um ângulo de 30o com um plano . Mostre que o ângulo que r faz com qualquer plano paralelo a mede 30o. 26. Seja r uma reta secante a um plano num ponto P, não perpendicular a . Mostre que o ângulo que r faz com é o menor ângulo dentre todos os ângulos que as retas contidas em passando por P fazem com r. 27. Mostre que dois planos são perpendiculares se, e somente se, duas retas respectivamente perpendiculares a cada um deles são ortogonais. 28. Mostre que se um plano contém uma reta perpendicular a um plano , então o plano contém uma reta perpendicular ao plano . 29. Seja O a projeção ortogonal de um ponto P sobre um plano . Considere uma circunferência de centro O contida em . Mostre que todas as retas tangentes a esta circunferência estão a uma mesma distância de P. 30. Dadas duas retas reversas, mostre que existe uma única reta perpendicular a ambas. 31. Sejam r e s retas reversas. Mostre que existem PQ ≤ XY, para quaisquer que sejam tais que 32. Seja r uma reta perpendicular a um plano . Mostre que todo plano que contém r é perpendicular a . 33. Seja r uma reta perpendicular a um plano num ponto O. Mostre que se s . é uma reta perpendicular a r passando em O, então Definição 53 (Mediador de um segmento de reta) Chama-se mediador de um segmento de reta o plano passando em seu ponto médio e perpendicular à reta que o contém. 34. Mostre que o mediador de um segmento é o conjunto dos pontos do espaço equidistantes de seus extremos. 35. Mostre que os mediadores dos lados de um triângulo inteceptam-se segundo uma reta. 36. Seja r uma reta perpendicular a um plano . Demonstre que se um plano é paralelo a , então r é também perpendicular a . 37. Se uma reta é perpendicular a dois planos em pontos distintos, mostre que esses planos são paralelos. 38. Se uma reta é perpendicular a dois planos num mesmo ponto, mostre que esses planos são coincidentes. 39. Seja P um ponto pertencente a uma reta r. Mostre que existe um único plano perpendicular a r passando por P. 40. Seja P um ponto não pertencente a uma reta r. Mostre que existe um único plano perpendicular a r passando por P. 41. Mostre que um plano é perpendicular a dois planos concorrentes se, e 32 AZEVEDO FILHO, M. F. DE somente se, ele é perpendicular à reta de interseção dos dois planos. 42. Dados um plano e uma reta r contida em , mostre que existe um único plano perpendicular a contendo r. 43. Dados um plano e uma reta r paralela a , mostre que existe um único plano perpendicular a contendo r. 44. Sejam A, B, C e D pontos distintos entre si pertencentes a um plano , . Mostre que se OA = OB = OC = OD, então A, B, C e D pertene, cem a uma mesma circunferência contida em cujo centro é a projeção ortogonal de O em 45. Mostre que o ângulo entre dois planos é igual ao ângulo que duas retas, respectivamente, perpendiculares a eles, fazem. 46. Mostre que o bissetor de um ângulo diedral cujas faces não são coplanares é o conjunto dos pontos equidistantes dos planos que contêm as respectivas faces do ângulo diedral pertencentes à região convexa determinada por ele. 47. Considere os ângulos que formam um triedro. Mostre que: a) a medida de cada um é menor do que a soma das medidas dos outros dois; b) a soma das medidas deles é menor do que 360o. 48. Uma figura é formada por quatro pontos A, B, C e D e pelos segmentos . Se os ângulos são retos, ela é uma figura plana? 49. Sejam três planos distintos. Mostre que as posições relativas possíveis dos planos são: a) Os três planos são paralelos. b) Dois deles são paralelos e o terceiro é concorrente a ambos, cortando-os segundo retas paralelas. c) Os três planos se cortam segundo uma reta. d) Os três planos se cortam dois a dois segundo três retas paralelas. e) Os três planos se cortam dois a dois segundo três retas concorrentes; o ponto comum às três retas é o único ponto comum aos três planos. Capítulo Cilindro, Cone e Esfera 2 Geometria Euclidiana Espacial 35 Objetivos • Saber definir cilindro, prisma, cone, tronco de cone, pirâmide e esfera. • Conhecer as propriedades básicas que envolvem cilindro, cone e esfera. • Saber reconhecer as posições relativas entre um plano e uma esfera, como também as posições relativas entre duas esferas. 1. Cilindro Entenderemos por figura plana qualquer um dos seguintes subconjuntos de um plano: polígono (convexo ou côncavo) mais a região delimitada por ele, disco fechado, elipse mais seu interior, etc., enfim, qualquer curva fechada, simples (isto é, sem auto-interseção), mais a região delimitada por ela. Vale ressaltarmos que a idéia de figura plana que acabamos de dar e um conceito primitivo, ou seja, sem definição, uma vez que não demos a definição de curva fechada simples e nem tampouco a definição da região delimitada por ela. Enfim, temos somente uma idéia. Definição 54 (Cilindro) Sejam: F uma figura contida num plano ; um plano paralelo a ; uma reta r que fura (conseqüentemente, fura também ) e h a distância entre e . O subconjunto do espaço que é a união de todos os segmentos de reta com uma das extremidades em F e a outra em , paralelos a r, chama-se cilindro de base F, com reta de inclinação r, entre e . Definimos a altura do cilindro como sendo h. Caso a reta r seja perpendicular a (e a ), o cilindro chama-se cilindro reto de base F, entre e . 36 AZEVEDO FILHO, M. F. DE Conforme demonstraremos adiante, a interseção do cilindro com o plano é uma figura congruente à base (veja a definição de figuras congruentes logo após o Teorema 59), a qual será também chamada de base. Definição 55 Chama-se prisma todo cilindro cuja base é um polígono. Num prisma, cada segmento paralelo à reta de inclinação partindo de um vértice da base com a outra extremidade no plano , e, os lados da base são chamados de aresta. As extremidades das arestas são denominadas de vértices do prisma e todo segmento de reta, que une dois vértices do prisma não pertencentes a uma mesma aresta, de diagonal do prisma. A reunião dos segmentos paralelos à reta de inclinação com uma das extremidades num lado da base e a outra em chama-se face lateral do prisma. Definição 56 Um cilindro chama-se circular se sua base é um disco. Geometria Euclidiana Espacial 37 Definição 57 Chama-se paralelepípedo todo prisma cuja base é um paralelogramo. Todo paralelepípedo reto cuja base é um retângulo é chamado de paralelepípedo retangular ou paralelepípedo retângulo. Definição 58 Chama-se cubo todo paralelepípedo retangular cuja base é um quadrado e cuja altura é igual ao lado da base. LEMA. Seja r uma reta que fura um plano . Então, toda reta paralela a r fura qualquer plano paralelo a . Prova. Seja s uma reta qualquer paralela a r. Seja o plano determinado por r e s. Como r fura , então e são concorrentes. Seja Temos: r, s e t são coplanares (estão contidas em ), r//s e t e r são concorrentes. Logo, t e s são concorrentes. O ponto de concorrência de t e s , segue-se que s fura . Pelo é comum a s e . Desde que Teorema 27, s fura qualquer plano paralelo a . Teorema 59 Seja um prisma entre os planos e . Se é um plano é uma figura congruente à base de . paralelo a e , entre e , então Prova. Seja a base de . Pelo lema, as retas que contêm os segmentos paralelos à reta de inclinação do prisma com uma das extremi- 38 AZEVEDO FILHO, M. F. DE Note que, pelo caso L.L.L. de congruentes de triânguos, figuras congruentes têm ângulos correspondentes congruentes. dades em F furam . E mais, o fazem em pontos pertencentes aos próprios segmentos. Sejam A, B e C vértices consecutivos quaisquer de F e A', B' e C' as respectivas interseções dos segmentos paralelos à reta de inclinação de partindo de A, B e C com . Basta mostrarmos que ABC A'B'C'. Temos: e como estão contidos em planos paralelos (respectivamente, em e ) e são e . Logo, ABB'A' é um paralelogramo. coplanares, então Pela mesma razão, BCC'B' e ACC'A' são paralelogramos. Logo, e daí, pelo caso L.L.L. de congruência de triângulos, segue-se que ABC A'B'C'. O teorema acima continua válido se trocarmos a palavra prisma por cilindro. Porém, precisamos de uma definição de figuras congruentes. Dois polígonos são congruentes quando é possível estabelecer uma correspondência biunívoca entre os vértices de um e os vértices do outro de tal maneira que os lados de um são todos congruentes aos lados correspondentes do outro e o mesmo acontecendo com os ângulos. Definição 60 (Congruência de figuras) Diremos que uma figura F é congruente a uma figura G e escrevemos F G se existe uma função bijetiva G tal que para quaiquer que sejam os pontos disf:F tintos A, B F. Antes, vamos recordar a definição de polígonos congruentes. Em outras palavras, uma figura é congruente à outra se é possível estabelecer uma correspondência biunívoca entre elas de tal maneira que segmentos correspondentes são congruentes. É possível demonstrar que a definição que acabamos de dar, no caso de F ser um polígono, é equivalente à definição de congruência de polígonos que recordamos há pouco. Não daremos a prova. Teorema 61 Seja um cilindro entre os planos e . Se é um é uma figura congruente plano paralelo a e , entre e , então à base de . Geometria Euclidiana Espacial 39 Prova. Seja a base de . Pelo lema do Teorema 59, as retas que contêm os segmentos paralelos à reta de inclinação do cilindro com uma das extremidades em F furam . E mais, o fazem em pontos pertencentes aos pró. Para mostrar que F F', basta estabelecerprios segmentos. Seja mos uma correspondência biunívoca entre F e F' de tal modo que segmentos correspondentes sejam congruentes. A correspondência é a seguinte: a cada associamos , em que A' é o ponto de interseção do seguinte segmento com : aquele paralelo à reta de inclinação do cilindro com uma das extremidades em A e a outra em . Sejam A, B F, distintos. Mostraremos que . Com efeito, temos: e como estão contidos em planos paralelos (respectivamente, em e ) e são coplanares, então . Logo, ABB'A' é um paralelogramo e, portanto, . 2. Cone Definição 62 (Cone) Sejam: F uma figura plana e V um ponto não pertencente ao plano que contém F. O subconjunto do espaço que é a união de todos os segmentos de reta com uma das extremidades em F e a outra em V chama-se cone de base F e vértice V. Definimos a altura do cone como sendo a distância do vértice ao plano que contém a base. Definição 63 Chama-se pirâmide todo cone cuja base é um polígono. Numa pirâmide, cada segmento que une um vértice da base e o vértice da pirâmide, e, os lados da base são chamados de aresta. Os triângulos cujos vértices são o vértice da pirâmide e dois vértices consecutivos da base são chamados de faces laterais da pirâmide. 40 AZEVEDO FILHO, M. F. DE Definição 64 Uma pirâmide chama-se regular se sua base é um n-ágono regular, n ≥ 4, e a projeção de seu vértice sobre o plano da base coincide com o centro desta. Definição 65 Chama-se tetraedro toda pirâmide cuja base é um triângulo. Um tetraedro é dito regular se todas as suas faces são triângulos equiláteros. Note que quatro pontos não coplanares são sempre vértices de um tetraedro e que qualquer face lateral de um tetraedro pode ser tomada como base. Note que as geratrizes de um cone circular reto têm a mesma medida. Definição 66 Um cone chama-se circular se sua base é um disco. Um cone circular é dito reto se a projeção ortogonal de seu vértice sobre o plano da base coincide com o centro dela. Todo segmento de reta que une o vértice de um cone circular reto a um ponto da fronteira da base chama-se geratriz do cone. LEMA. Sejam: V um ponto não pertencente a um plano ; A, B , um plano paralelo a entre V e ; e distintos; . Então, V A'B' ~ V AB com razão de semelhança igual a Geometria Euclidiana Espacial 41 Prova. Temos: , pois estão contidas em planos paralelos e desde que são coplanares segue-se que são paralelas. Logo, V A'B' ~ V AB. Sendo A e B quaisquer pontos distintos em , fixemos A e façamos B igual à projeção de V em . Desse modo, B' é a projeção de V em . Então, a razão de semelhança é igual a Teorema 67 Seja uma pirâmide de vértice V e base F contida num é uma figura plano . Se é um plano paralelo a , entre V e , então semelhante a F cuja razão de semelhança é Prova. As retas que contêm os segmentos com uma das extremidades em F e o outra em V furam . E mais, o fazem em pontos pertencentes aos próprios segmentos. Sejam A, B e C vértices consecutivos quaisquer de F e A', B' e C' as respectivas interseções dos segmentos que unem V a A, B e C com . 42 AZEVEDO FILHO, M. F. DE Antes, vamos recordar a definição de polígonos semelhantes. Basta mostrarmos que ABC ~ A'B'C' com razão de semelhança igual a Pelo lema, temos: V A'B' ~ V AB, V C'B' ~ V CB e V A'C' ~ V AC com razão de semelhança igual a Desse modo, segue-se que Pelo caso L.L.L. de semelhança de triângulos, decorre o resultado. O teorema acima continua válido se trocarmos a palavra pirâmide por cone. Porém, precisamos de uma definição de figuras semelhantes. Dois polígonos são semelhantes quando é possível estabelecer uma correspondência biunívoca entre os vértices de um e os vértices do outro de tal maneira que os lados de um são proporcionais aos lados correspondentes do outro e ângulos correspondentes são congruentes. A razão de semelhança é a razão de proporcionalidade entre os lados do primeiro e os lados do segundo. Definição 68 (Semelhança de figuras) Sejam F e G figuras e k um número real positivo. Diremos que F é semelhante a G com razão de semelhanou, simplesmente, se existe uma função ça k e escrevemos tal que bijetiva para quaisquer que sejam os pontos distintos A, B F. Geometria Euclidiana Espacial 43 Em outras palavras, uma figura é semelhante à outra se é possível estabelecer uma correspondência biunívoca entre elas de tal maneira que segmentos correspondentes são proporcionais. É possível demonstrar que a definição que acabamos de dar, no caso de F ser um polígono, é equivalente à definição de semelhança de polígonos que recordamos há pouco. Não daremos a prova. Outro fato que não iremos demonstrar e que utilizaremos na unidade subseqüente acerca de figuras semelhantes é o seguinte: a razão entre as áreas de duas figuras semelhantes é igual ao quadrado da razão de semelhança. Teorema 69 Seja . Se um cone de vértice V e base F contida num plano é um plano paralelo a , entre V e , então é uma figura seme- lhante a F cuja razão de semelhança é Prova. As retas que contêm os segmentos com uma das extremidades em F e o outra em V furam . E mais, o fazem em pontos pertencentes Para mostrar que F ~ F', basta aos próprios segmentos. Seja estabelecermos uma correspondência biunívoca entre F e F' de tal modo que segmentos correspondentes sejam proporcionais com razão de proporcionalidade Acorrespondência é a seguinte: a cada associamos , em que A' é o ponto de interseção do seguinte segmento com : aquele com uma das extremidades em A e a outra em V. Sejam A, B F, disDe fato, isto é decorrente do tintos. Mostraremos que lema do Teorema 67. Definição 70 Sejam: um cone de vértice V e base F contida num plano e um plano paralelo a , entre V e . O subconjunto de dos pontos que se situam entre e chama-se tronco do cone determinado por . A distância de bases. dos planos e chamaremos de altura do tronco, e, Note que, pelo caso L.L.L. de semelhança de triãngulos, figuras semelhantes têm ângulos correspondentes congruentes. 44 AZEVEDO FILHO, M. F. DE 3. Esfera Definição 71 (Esfera) Sejam O um ponto e r um número real positivo. O conjunto dos pontos do espaço cuja distância a O é menor do que ou igual a r chama-se esfera de centro O e raio e será denotada por (O; r). Duas esferas são ditas concêntricas se possuem o mesmo centro. Definição 72 Dados uma esfera e um ponto P, dizemos que P é um ponto interior ou exterior de se, respectivamente, d(P,O) < r ou d(P,O) > r. O conjunto de todos os pontos interiores de é chamado de interior de e é denotado por int e o dos pontos exteriores é chamado de exterior de e é denotado por ext . Definição 73 O subconjunto de uma esfera formado pelos pontos cuja distância ao centro é igual ao raio chamaremos de superfície da esfera. Teorema 74 Se um plano tem, pelo menos, dois pontos em comum com uma esfera, então a interseção dos dois é um disco cujo centro é a projeção ortogonal do centro da esfera no plano e cuja circunferência é a interseção deste com a superfície da esfera. Prova. Sejam: (O; r) a esfera; o plano, e, A e B pontos distintos pertencentes a e . Seja O' a projeção ortogonal de O em . Como A e B são tal que distintos, então O' ≠ A ou O' ≠ B. Digamos que O' ≠ A. Seja C . O'C está bem definido e é positivo, pois d(O,O') < d(O,A) ≤ r. E mais, d(O,C) = r, pois caso O ≠O' o triângulo OO'C é retângulo em O'. Mostraremos que o disco contido em de centro O' e raio r' = O'C é . De fato, seja . Geometria Euclidiana Espacial 45 Temos: , por conseguinte, . Tomemos agora . , donde, Temos: , portanto, . Isso mostra que . Seja a circunferência de . é a interseção de com a superfície de . Para provar isso é só seguir os mesmos passos que foram utilitrocando-se ≤ por =. zados na demonstração de que Definição 75 Diremos que uma esfera e um plano são secantes se eles têm em comum, pelo menos, dois pontos; se eles têm em comum apenas um ponto diremos que são tangentes naquele ponto e se não tiverem ponto em comum diremos que são exteriores. Teorema 76 Sejam (O; r) uma esfera, um plano e é tangente a em P P pertence à superfície de e . Então, . Prova. ( ) Seja O' a projeção de O em . Afirmamos que O' = P. Por absurdo, suponhamos que O' ≠ P. Então, O = O' ou o triângulo OO'P é re, tângulo em O'. Em ambos os casos, temos: OO' < OP ≤ r, donde, . Portanto, O' = P e, por o que é uma contradição ao fato de . Não podemos ter P = O, pois se assim o conseguinte, P = O ou fosse, tomando-se em um ponto Q tal que 0 < d(O,Q) ≤ r, teríamos outro . Vamos agora mostrar que ponto comum a e . Logo, P ≠ O e PO = r. Por absurdo, suponhamos que PO < r. Seja A tal que gulo OPA é retângulo em P, teremos: seria outro ponto comum a e . Desde que o triân, donde, A ( )Seja Q um ponto qualquer de distinto de P. Dado que , segue-se que OP < OQ e, como P pertence à superfície de , então r < OQ. Conclusão: os pontos de , exceto P, não pertencem a . Portanto, . 46 AZEVEDO FILHO, M. F. DE Definição 77 Consideremos agora as superfícies de duas esferas distintas. Se a interseção delas possuir exatamente um ponto diremos que elas são tangentes e se possuir pelo menos dois pontos diremos que são secantes. Teorema 78 Sejam 1(O1; r1) e 2(O2; r2) esferas não concêntricas e P O1, um ponto comum às superfícies de 1 e 2. Então, elas são tangentes O2 e P são colineares. Prova. ( ) Por absurdo, suponhamos que O1, O2 e P não são colineares. Consideremos o plano determinado por O1, O2 e P. Podemos tomar no semi-plano , um ponto Q tal que QO1 = r1 e oposto ao que contém P, em relação a . QO2 = r2, já que Assim sendo, as superfícies de hipótese. 1 e 2 são secantes, o que contraria a ( )Por absurdo, seja Q um ponto comum às superfícies de 1 e 2 tal está que Q ≠ P. Desde que O1 e O2 são equidistantes de P e Q, vem que . Logo, contrariando a hipótese. contida no plano mediador de Teorema 79 Dadas duas esferas cêntricas, temos: i) as superfícies de ii) as superfícies de 1 1 iii) as superfícies de ou e e 2 2 1 são tangentes não conou são secantes e 2 têm interseção vazia Prova. i) ( ) Seja P o ponto comum às superfícies de 1 e 2. Pelo teoreou ma anterior, P, O1 e O2 são colineares. Por conseguinte, . É imediato que, no primeiro caso, tem-se d(O1,O2 ) = r1 + r2 e, no segundo, d(O1,O2 ) = |r1 + r2|. ( ) Se d(O1,O2 ) = r1 + r2, tomemos tal que O1P = r1. Desse modo, vem que O2P = r2. Portanto, P é um ponto comum às superfícies de 1 Geometria Euclidiana Espacial 47 e 2. Como P, O1 e O2 são colineares, o teorema anterior garante o resultado. Suponhamos agora que d(O1,O2 ) = |r1 – r2|. Assim, d(O1,O2 ) = r1 – r2 ou d(O1,O2 ) = |r2 – r1|. No primeiro caso, tomemos tal que O2 se situa entre O1 e P e O2P = r2 e, no segundo, tomemos P tal que O1 se situa entre O2 e P e O1P = r1. No primeiro caso, vem que O1P = r1 e, no segundo, O2P = r2.Logo, em ambos os casos, temos que P é um ponto comum às superfícies de 1 e 2. Como P, O1 e O2 são colineares, segue-se que {P} é a interseção das superfícies de 1 e 2. ii) ( ) Seja P um ponto comum às superfícies de 1 e 2. Pelo teorema anterior, P, O1, e O2 não são colineares e, portanto, o resultado segue-se pela desigualdade triangular. ( ) Consideremos um plano qualquer que contenha O1 e O2. Podemos , respectivamente, um ponto tomar em cada semi-plano, em relação a P e um ponto Q tais que PO1 = r1, PO2 = r2, QO1 = r1 e QO2 = r2, já que |r1 – r2| < O1O2 < r1 + r2. Logo, as superfícies de 1 e 2 são secantes. iii) É óbvio. Sejam 1 e 2 as respectivas superfícies de 1 e . 2 Observação 80 No caso em que d(O1,O2 ) = r1 + r2, temos que os pontos de uma, exceto o de tangência, P, são exteriores à outra. Com efeito, seja Q ≠ P tal que Q 1, isto é, d(Q,O1) = r1. Como , vem que d(O1,O2 ) < d(O1,Q) + d(Q,O2), donde r1 + r2 < . Nesse caso, dizer1 + d(Q,O2) e, portanto, r2 < d(Q,O2), ou seja, mos que 1 e 2 são tangentes externas. Observação 81 No caso em que d(O1,O2 ) = |r1 – r2|, então os pontos, exceto o de tangência, P, daquela que tiver o menor raio, são interiores à outra enquanto que os pontos, exceto o de tangência, daquela que tiver o maior raio, são exteriores à outra. 48 AZEVEDO FILHO, M. F. DE De fato, digamos que r1 < r2. Seja Q ≠ P tal que . Desde (verifique isto), segue-se que d(Q,O2 ) < d(O1,Q) + d(O1,O2 ). que , então d(Q,O2 ) < r2, e, se , então r2 < d(Q,O1), É imediato que se como queríamos provar. Nesse caso, dizemos que aquela de menor raio é tangente interna à outra e que esta é tangente externa à primeira. Observação 82 Se d(O1,O2 ) > r1 + r2, então os pontos de uma são exteriores . Temos que r1 + r2 < d(O1,O2 ) ≤ d(O1,Q) à outra. De fato, seja ,então d(Q,O2 ) > r2, e, se , + d(Q,O2 ), donde, decorre que se então d(O1 ,Q) > r1. Dizemos, nesse caso, que elas são externas. Observação 83 Se d(O1,O2 ) < |r1 – r2|então os pontos daquela de menor raio são interiores à outra enquanto que os pontos desta são exteriores à primeira. Com efeito, para fixarmos as idéias, digamos que r1 < r2. Seja . Posto que d(Q,O2 ) ≤ d(O1,Q ) + d(O1,O2 ) < d(O1,Q) + , então d(Q,O2 ) < r2 , e, se , então d(O1 |r1 – r2|, decorre que se ,Q) > r1. Nesse caso, dizemos que a de menor raio é interna à outra e que esta é externa à primeira. Se duas esferas coplanares e distintas são concêntricas, é imediato que os pontos daquela de menor raio são interiores à outra ao passo que os Geometria Euclidiana Espacial 49 pontos da superfície desta são exteriores à primeira. Neste caso, diremos que a superfície da primeira é interna à da segunda e que a superfície desta é externa à da primeira. Teorema 84 Sejam 1(O1;r1) e 2 (O2;r2) duas esferas não concêntricas e cujas superfícies são secantes. Então, estas se interceptam segundo uma circunferência cujo centro é a projeção ortogonal de O1 e de O2 no plano que a contém. Prova. Seja P um ponto comum às superfícies de 1 e 2. Como elas . Sejam o plano passando são secantes, temos que P não pertence a e O o pé da perpendicular em . Temos: por P e perpendicular a O ≠ O1 ou O ≠ O2. Digamos que O ≠ O1. Seja a circunferência contida em de centro O e raio r = OP. Afirmamos que a interseção das superfícies é . Seja Q um ponto qualquer, distinto de P, na interseção. Q não pertence a . Mostraremos que . Com efeito, desde que O1O2P O1O2Q, segue-se que donde, e, portanto, PO1O QO1O. Posto que é reto, decorre que também o é e, portanto, . Uma vez . Tomemos agora . Devemos mosque r = PO = QO, vem que trar que Q pertence à interseção. De fato, como QO = r = PO, então PO1O , logo, , QO1O, donde, QO1 = PO1= r1 e O1O2Q e assim QO2 = PO2= r2. Assim sendo, Q por conseguinte, O1O2P pertence à interseção das superfícies de 1 e 2. Por conseguinte, a interseção das superfícies das esferas é uma circunferência cujo centro é a projeção ortogonal de O1 e de O2 no plano que a contém. 50 AZEVEDO FILHO, M. F. DE Síntese do Capítulo Estabelecemos as definições de cilindro, prisma, cone, tronco de cone, pirâmide e esfera. Demos os teoremas respeitantes às propriedades básicas que envolvem cilindro, cone e esfera. Demonstramos teoremas que caracterizam as posições relativas entre um plano e uma esfera, como também as posições relativas entre duas esferas. Atividades de avaliação 1. Qual o comprimento da maior diagonal de uma caixa na forma de um paralelepípedo retangular cujas dimensões são 3cm, 4cm e 6cm. um segmento, também de me2. Seja ABCD um quadrado de lado a e dida a, perpendicular ao plano do quadrado. Calcule a medida do diedro determinado pelos triângulos PCB e PCD. 3. Em um prisma, a soma dos ângulos internos de todas as faces é igual a 2880o. Quantas faces laterais possui o prisma? 4. Determine o número de arestas, de vértices, de faces e a soma dos ângulos de todas as faces de um prisma cuja base é um polígono regular em que a soma de seus ângulos internos é igual a 3600o. 5. Determine a área da figura que é a interseção de um plano com um cubo de aresta a, sabendo que o plano contém apenas três vértices do cubo. 6. Sejam ABC e A'B'C' as bases de um prisma reto cuja altura é h, em que são perpendiculares aos planos das bases. Sabendo que ABC é equilátero de lado a, determine a área do triângulo ABC'. 7. A base de um prisma reto é um hexágono regular de lado a. Suas faces laterais são quadrados. Calcule o comprimento da maior diagonal desse prisma. 8. Mostre que as faces laterais de uma pirâmide regular são triângulos isósceles congruentes entre si. 9. Considere uma pirâmide regular cuja base é quadrada. Suponha que a razão entre o perímetro da base e a altura seja igual a , que é a mesma relação guardada entre o perímetro de um círculo e seu raio. (Essas são as proporções da grande pirâmide do Egito. Algumas pessoas acreditam que as pirâmides com essa forma têm o poder de concentrar energia cósmica e, portanto, acelerar os processos biológicos de cura de doenças.). Expresse: Geometria Euclidiana Espacial 51 a) a tangente do ângulo que as faces laterais fazem com a base; b) a aresta lateral em função da aresta da base; c) o cosseno dos ângulos internos das faces laterais dessa pirâmide; d) o cosseno do ângulo formado por duas faces laterais contíguas. 10. Um tronco de pirâmide regular tem como bases triângulos equiláteros cujos lados medem, respectivamente, 2cm e 4cm. Se a aresta lateral do tronco mede 3cm, qual o valor de sua altura? 11. Considere um cubo de bases ABCD e EFGH e arestas laterias , Suponha que as arestas medem 3m e sejam M, N e , , , AM = AN = 2m e BP = P pontos tais que 0,5m. Calcule o perímetro da seção que o plano passando por M, N e P determina no cubo. 12. Mostre que não existe uma pirâmide regular cujas faces laterais são triângulos equiláteros e cuja base tem mais de cinco lados. 13. Seja A o vértice de uma pirâmide cuja base é um polígono regular P. Se A é equidistante dos vértices de P, demonstre que a projeção ortogonal de A, no plano que contém P, coincide com seu centro. 14. Quatro superfícies de esfera, com mesmo raio, são tangentes entre si. Mostre que seus centros são vértices de um tetraedro regular. 15. Sejam A e B pontos distintos. Qual é o subconjunto do espaço formado é reto? pelos pontos X tais que 16. Demonstre que por quatro pontos não coplanares passa uma única superfície de esfera. 17. Mostre que existe um único ponto equidistante dos vértices de um tetraedro qualquer, chamado de circuncentro do tetraedro, o qual é o centro de uma esfera cuja superfície contém seus vértices, chamada de esfera circunscrita a ele. 18. Mostre que existe um único ponto equidistante das faces de um tetraedro qualquer, chamado de incentro do tetraedro, o qual é o centro de uma esfera que tangencia sua faces, chamada de esfera inscrita nele. 19. Os itens a seguir, deste exercício, têm como objetivo garantir a existência dos tetraedros regulares e também estabelecer algumas de suas propriedades. a) Mostre que existe um tetraedro regular. Determine sua altura h em função de sua aresta a. b) Mostre que são ortogonais duas arestas opostas do tetraedro regular. c) Mostre que a reta que passa nos pontos médios de duas arestas opostas do tetraedro regular é a perpendicular comum a ambas. 52 AZEVEDO FILHO, M. F. DE d) Mostre que existe um único ponto equidistante dos vértices e das faces do tetraedro regular, chamado de centro do tetraedro, o qual é o centro comum das esferas inscrita e circunscrita a ele. Calcule, em função de a, os raios R e r, respectivamente, das esferas circunscrita e inscrita nele, bem como seus ângulos diedrais. e) Mostre que os centros das faces do tetraedro regular são vértices de outro tetraedro regular. 20. Demonstre que existem paralelepípedos retangulares e cubos. 21. Mostre que existe um único ponto equidistante dos vértices e das faces de um cubo, chamado de centro do mesmo, o qual é o centro comum das esferas inscrita e circunscrita a ele. Calcule, em função da aresta a do cubo, os raios R e r, respectivamente, das esferas circunscrita e inscrita nele. 22. Uma pirâmide de base triangular tem faces laterais isósceles. Sabe-se que a área da base é igual ao quadrado da altura h da pirâmide. Se r é o raio da esfera inscrita nessa pirâmide, determine a razão h/r. 23. Um cone circular reto tem altura 12cm e raio da base 5cm. Quanto mede o raio da esfera inscrita nele? 24. Um cone circular reto tem altura h e raio da base r. Quanto mede o raio da esfera inscrita nele? 25. Sejam A, B, C e D os vértices da base de um cubo e A', B', C' e D' os vértices correspondentes da outra base. a) Mostre que os pontos médios das seguintes arestas são coplanares: b) Mostre que os pontos médios referidos no item anterior são vértices de um hexágono regular. Capítulo Volume e área de superfície 3 Geometria Euclidiana Espacial 55 Objetivos • Conhecer as fórmulas básicas envolvendo volume e área de superfície do cilindro, prisma, cone, tronco de cone, pirâmide e esfera. • Saber demonstrar as fórmulas básicas envolvendo volume e área de superfície do cilindro, prisma, cone, tronco de cone, pirâmide e esfera. • Saber aplicar as fórmulas que envolvem volume e área de superfície na resolução de problemas. Arquimedes, matemático grego, nasceu em 287 a.C. na cidade de Siracusa, na ilha de Sicília. Estudou em Alexandria e voltou à cidade natal onde permaneceu até a morte que ocorreu em 212 pela espada de um soldado romano. Ficou famoso pelas suas invenções bélicas. É o autor do princípio da alavanca, sobre o qual ficou conhecida a seguinte frase de Arquimedes: "Dêem-me um ponto de apoio e moverei o mundo". É também autor do princípio segundo o qual um corpo imerso num líquido sofre a ação de uma força, de baixo para cima, igual ao peso da quantidade de líquido que desloca. Este ficou conhecido como o princípio de Arquimedes que utilizou para descobrir se a coroa do rei Híeron II fora confeccionada de ouro puro ou não. Arquimedes deu uma grande contribuição à geometria espacial. Ele é responsável pela descoberta das fórmulas do volume e área da superfície dos principais sólidos geométricos tais como a esfera, cilindro, cone, etc. É este assunto que iremos abordar nesta unidade. Figura 1 – Arquimedes com o compasso 56 AZEVEDO FILHO, M. F. DE 1. A Noção de Volume Entenderemos por sólido qualquer um dos seguintes subconjuntos do espaço: cilindro, cone, esfera, poliedro (que iremos definir na próxima unidade) ou qualquer superfície fechada, simples (isto é, sem auto-interseção), mais a região delimitada por ela. Note que, pelo caso de L.L.L. de congruência de triângulos, sólidos congruentes têm ângulos correspondentes congruentes. Note que qualquer face de um paralelepípedo retangular pode ser tomado como base. Vale salientarmos que a idéia de sólido que acabamos de dar é um conceito primitivo, ou seja, sem definição, uma vez que não demos a definição de superfície fechada simples e nem tampouco a definição da região delimitada por ela. Enfim, temos somente uma idéia. Outro conceito primitivo que iremos considerar é o de volume de um sólido. O volume de um sólido é a quantidade de vezes que o cubo de aresta unitária "cabe" nele. O cubo de aresta unitária será chamado de unidade de medida de volume. Se a unidade de medida de comprimento utilizada é o metro, chamaremos a unidade de medida de volume (que é o cubo de aresta unitária) de metro cúbico e o denotaremos por 1m3. Assim, medir o volume de um sólido, com essa unidade de medida de volume, consiste em saber quantos metros cúbicos há nele. A idéia é de comparação dos sólidos com o cubo de aresta unitária no que tange ao lugar que eles ocupam no espaço. Adotaremos a notação (S)para denotar o volume de um sólido S. Definição 85 (Congruência de sólidos) Diremos que um sólido S é conS' se existe uma função bijetiva gruente a um sólido S' e escrevemos S tal que para quaiquer que sejam os pontos distintos A, B S. Em outras palavras, um sólido é congruente à outro se é possível estabelecer uma correspondência biunívoca entre eles de tal maneira que segmentos correspondentes são congruentes. Diremos que um sólido S está decomposto como soma de dois sólidos S1 e S2 se S é a união de S1 e S2 e S1 S2 é subconjunto da superfície de ambos. Admitiremos que sólidos congruentes têm mesmo volume e que se um . sólido S está decomposto como soma de S1 e S2, então Também iremos admitir que paralelepípedos retangulares com bases congruentes e mesma altura são congruentes e, conseqüentemente, têm mesmo volume. Geometria Euclidiana Espacial 57 2. Volume do Paralelepípedo Retangular Considere um paralelepípedo retangular cujas arestas adjacentes da base medem, respectivamente, 5 e 4 unidades de medida de comprimento e cuja altura mede 3. Quantos cubos de aresta unitária "cabem’’ nele? Ou seja, qual seu volume? Vejamos. É uma questão de contagem. Vamos decompor o paralelepípedo em quatro subparalelepípedos. Cada um desses subparalelepípedos contém 5 x 3 cubos de aresta unitária. Portanto, no total, o paralelepípedo original contém 5 x 3 x 4 unidades de medida de volume, isto é, seu volume é 60. Enfim, um paralelepípedo retangular cujas arestas adjacentes da base medem, respectivamente, m e n unidades de medida de comprimento e cuja altura mede h, em que m, n e h são números inteiros, tem volume igual ao produto mnh. Esse resultado continua válido para m, n e h números reais positivos quaisquer. LEMA. Seja (an) uma seqüência de números reais e a, b R tais que para todo n. Então, a = b. Prova. Mostraremos que não temos a < b e nem b < a. Se a < b, es. Assim, . Sendo an ≤ a, vem colhamos um inteiro positivo , donde, , o que é uma contradição! Se que b < a, de modo análogo, também chegaremos a uma contradição. Logo, a = b. É o que pretendemos mostrar em seguida. 58 AZEVEDO FILHO, M. F. DE Teorema 86 Sejam P e P' paralelepípedos retangulares de bases congruentes e alturas a e a', respectivamente. Então, Prova. Sejam XYZW e X'Y'Z'W' as bases de P, em que XX' = YY' = ZZ' = WW' = a, E, ABCD e A'B'C'D' as bases de P', em que AA' = BB' = CC' = DD' = a'. Escolhamos a altura que for menor do que ou igual à outra. Digamos em n partes congruenque a' ≤ a. Para cada inteiro positivo n, dividamos com entre para cada tes, isto é, sejam (tomamos e ) tais que para . todo Seja . Por cada ponto de divisão consideremos o plano pa- ralelo à base. Estes interceptam P' segundo retângulos congruentes à base. Assim sendo, o paralelepípedo P' fica decomposto em n paralelepípedos congruentes entre si. Desse modo, o volume de cada um deles é igual a Consideremos agora a semi-reta existem mos A0 = X) tais que com . e o número real positivo xn. Então, entre e para todo (toma- Geometria Euclidiana Espacial 59 Além disso, posto que , vem que existe um in- teiro positivo mn tal que X' = Amn ou X' está situado entre Amn e Amn +1. Tem-se ainda que , donde, . Fazendo . Por cada , vem que , consideremos o plano paralelo à base. Es- tes determinam paralelepípedos todos congruentes aos paralelepípedos da decomposição de P' (por terem bases congruentes e mesma altura todos com mesmo volume ), portanto, . Desse modo, o volume de P é maior do que ou igual à soma de mn desses volumes e é menor do que a soma de mn + 1 dos mesmos. Em símbolos, temos: donde, , . Posto que e para cada inteiro positivo n, segue-se, pelo lema, que Corolário 1 Sejam P um paralelepípedo retangular cujas arestas adjacentes da base medem, respectivamente, a e b e cuja altura mede c, e, P' um paralelepípedo retangular cujas arestas adjacentes da base medem, respectivamente, a' e b' e cuja altura mede c'. Então, Prova. Sejam P" um paralelepípedo retangular cujas arestas adjacentes da base medem, respectivamente, b e c e cuja altura mede a', e, P" um paralelepípedo retangular cujas arestas adjacentes da base medem, respectivamente, a' e c e cuja altura mede b'. Comparando P com P", P"com P"' e P"' com P' teremos: Multiplicando-se estas igualdades membro a membro chega-se ao resultado. Corolário 2. Seja P um paralelepípedo retangular cujas arestas adjacentes da base medem, respectivamente, a e b e cuja altura mede c. Então, Prova. Basta fazer no corolário anterior P' igual a um cubo de aresta unitária. Utilizando o Corolário 2, podemos concluir que o volume de um paralelepípedo retangular é igual ao produto da área da base pela altura. 60 AZEVEDO FILHO, M. F. DE 3. Volume do Cilindro, Cone e Esfera Chamaremos de plano horizontal todo aquele paralelo ou coincidente com um certo plano que fixamos (implicitamente ou explicitamente) como referencial numa discussão. A seguir, enunciaremos um axioma conhecido por "Princípio de Cavalieri", com o qual iremos deduzir as fórmulas que darão os volumes do cilindro, do cone e da esfera. Princípio de Cavalieri. “Sejam S e S' sólidos. Se todo plano horizontal intercepta S e S' segundo figuras com mesma área, então S e S' têm mesmo volume.” Teorema 87 O volume de um cilindro é igual ao produto da área da base pela altura. Prova. Seja um cilindro entre os planos e de base F e altura h, . Considere um paralelepípedo , retangular, cuja base R está em que contida em e tem a mesma área de F, cuja altura seja h e esteja no mesmo semi-espaço (determinado por ) em que se encontra . Consideraremos o conjunto vazio ou um conjunto unitário como uma figura de área nula para efeito do enunciado do princípio de Cavalieri. Considere um plano paralelo a e , entre e . Pelo Teorema Geometria Euclidiana Espacial 61 61, . Como F e R têm mesma área, segue-se têm mesma área. Pelo princípio de Cavalieri, o as secções cilindro e o paralelepípedo têm mesmo volume. Desde que o volume de , de acordo com o Corolário 2 do Teorema 86, é o produto da área de R por h, decorre que o volume de é o produto da área de R por h e, posto que R e F têm mesma área, segue-se que o volume de é o produto da área de F por h. Teorema 88 Dois cones têm mesmo volume se têm mesma altura e suas bases têm mesma área. Prova. Coloquemos as bases dos dois cones num mesmo plano, digamos, , e seus vértices num mesmo semi-espaço determinado por . Sejam: e ' os cones, F e F' as respectivas bases, V e V' os respectivos vértices e h a altura comum. Para demonstrar que e ' têm o mesmo volume utilizaremos o princípio de Cavalieri. Seja um plano paralelo a , entre V (ou V') e e têm mesma área. e h' = d(V, ). Basta mostrarmos que a Pelo Teorema 69, vem que com razão de semelhança igual e com razão de semelhança também igual a . Desde que a razão entre as áreas de duas figuras semelhantes é igual ao quadrado da razão de semelhança, segue-se que Posto que área(F) = área(F'), decorre que área = área . Teorema 89 O volume de um cone é igual a um terço da área da base pela altura. Prova Inicialmente, demonstraremos o teorema para o caso do cone ser um tetraedro. Consideremos então um tetraedro de base um triângulo ABC, de vértice D e altura h. 62 AZEVEDO FILHO, M. F. DE Sejam o plano que contém ABC, o plano paralelo a passando por D e B' e C' os respectivos pontos de interseção das retas paralelas a passando por B e C com . Considere o prisma entre e cuja reta de e cuja base em é ABC. A base de em é DB'C'. Obinclinação é serve que está decomposto como soma dos seguintes três tetraedros: , o tetraedro ' de vértices em B, C, D e B' e o tetraedro '' de vértices em B', C', D e C. Vamos mostrar que esses três tetraedros têm mesmo volume. Com efeito, tomando ABD como base de , B'DB como base de ' e C como vértice comum a e ', então e ' têm bases congruentes e mesma altura, logo, pelo teorema anterior, têm mesmo volume. Pela mesma razão, ' e '' têm mesmo volume se considerarmos BB'C como base de ', C'CB' como base de '' e D como vértice comum a ' e ''. Posto que , ' e '' têm mesmo volume e está decomposto como soma destes tetraedros, seguePor conseguinte, o teorema -se que vale para tetraedros. Para demonstrarmos que o resultado é válido para um cone qualquer é só considerarmos um tetraedro com mesma altura de e cuja base tenha a mesma área da base de . O resultado decorre do teorema anterior. Corolário 1 O volume de um cone circular é igual a o raio da base e h é a altura do cone. , em que r é Corolário 2 O volume de uma pirâmide, cuja base é um polígono regu, em que p e a são, respectivamente, o semi-perímetro e o lar, é igual a apótema da base e h é a altura da pirâmide. Prova. O resultado segue-se pelo fato da área de um polígono regular ser igual ao produto de seu semi-perímetro pelo seu apótema. Corolário 3 O volume de um tronco de pirâmide, cujas bases são polígonos regulares, cuja altura é h, cujos semi-perímetros das bases maior e menor, respectivamente, são P e p, e, cujos apótemas das bases maior e menor, respectivamente, são A e a é igual a Geometria Euclidiana Espacial 63 Prova. Seja h' a altura da pirâmide. Então, a razão de semelhança entre a base menor e a maior é , portanto, donde, seguem-se que A pirâmide original está decomposta como soma do tronco mais uma pirâmide cuja base é a base menor do tronco e cuja altura é h' – h. Por conseguinte, o volume do tronco é igual a Corolário 4 O volume de um tronco de cone circular cuja altura é h e cujos raios das bases são R e r é igual a Prova. Seja n > 2 um inteiro. Consideremos um polígono regular de n lados inscrito na base maior, digamos, de raio R, e sejam Pn e An, respectivamente, seu semi-perímetro e seu apótema. Considere também o polígono regular de n lados inscrito na base de raio r correspondente ao anterior e sejam pn e an, respectivamente, seu semi-perímetro e seu apótema. Então, o volume do tronco da pirâmide cujas bases são esses polígoO volume do tronco do cone circular nos vale Desde que é o limite desse valor quando quando , decorre que o volume do tronco do cone circular é igual a Teorema 90 O volume de uma esfera de raio r é igual a Prova. Sejam O o centro da esfera, t uma reta passando em O, e, P e Q e OP = r = OQ. Sejam pontos distintos em t tais que O é ponto médio de 64 AZEVEDO FILHO, M. F. DE e os planos perpendiculares a t passando, respectivamente, por P e Q. Assim, e são paralelos e são tangentes à esfera, respectivamente, em P e Q. Seja um cilindro circular entre e tendo como reta de inclinação t (portanto, reto) cujos raios das bases são iguais a r. Seja V o ponto médio do segmento de reta que une os centros das bases de . Considere os cones com o vértice comum V e cujas respectivas bases são as bases de . Utilizaremos o princípio de Cavalieri para mostrar que o volume da esfera é igual ao volume do sólido S formado pelos pontos de não interiores à reunião dos dois cones. Seja um plano qualquer paralelo a e , entre e . Mostraremos que o disco de interseção de com a esfera tem a mesma área (que é uma coroa circular). Seja h a distância entre e . de Faremos a demonstração supondo h < r. O raciocínio que iremos empregar também se aplica ao caso de r ≤ h, o qual omitiremos. Seja y o raio do disco de interseção de com a esfera. Usando o Teorema de Pitágoras, podemos concluir que y2 = 2rh – h2, por conseguinte, a área do disco é igual . Seja x o raio do círa (2rh – h2). Vamos agora calcular a área de , culo menor da coroa. Usando semelhança, chegaremos à relação donde, x = r – h. Sendo r o raio do círculo maior da coroa, então sua área é . Logo, o disco de interseção de igual a com a esfera tem a mesma área de . Assim, o volume da esfera é igual menos o volume dos dois ao volume de S que, por sua vez, é igual a cones, ou seja, 4. Área de Superfície Neste parágrafo, iremos deduzir fórmulas que fornecerão a área da superfície de certos sólidos. Comecemos pela soma das áreas das faces laterais de um prisma reto. Geometria Euclidiana Espacial 65 Teorema 91 A soma das áreas das faces laterais de um prisma reto é igual ao produto do perímetro da base pela altura. Prova. Cada face lateral é um retângulo cuja altura h é a altura do prissão os lados ma e cuja base é um lado da base do prisma. Se da base do prisma, então soma das áreas das faces laterais dele é igual a isto é, o produto do perímetro da base pela altura. Teorema 92 A área da superfície lateral de um cilindro reto é igual ao produto do perímetro da base pela altura. Prova. A idéia é aproximarmos o contorno da base, que é uma curva fechada simples, por linhas poligonais fechadas cujos vértices pertençam a ele. Assim, as áreas das superfícies laterais dos prismas retos determinados por essas linhas poligonais fechadas com mesma altura do cilindro dado se aproximam da área da superfície lateral dele. Quanto mais aumentarmos o número n de lados da linha poligonal melhor será a aproximação. Fazendo , o perímetro da linha poligonal tenderá ao perímetro da base do cilindro e a área da superfície lateral do prisma determinado pela linha tenderá à área da superfície lateral do cilindro. Em símbolos, se 2pn e 2p são, respectivamente, os perímetros da linha e da base do cilindro, e, An e A são, respectivamente, as áreas das superfícies laterias do prisma e do cilin2p e An A quando . Temos que An = 2pnh, em dro, então 2pn , que h é a altura do cilindro e do prisma. Fazendo, nesta relação, obtemos A = 2ph. Corolário. A área da superfície lateral de um cilindro circular reto cuja altura é h e cujo raio da base é r é igual a 2 rh. Teorema 93 A soma das áreas das faces laterais de uma pirâmide regular é igual a em que p e a são, respectivamente, o semi-perímetro e o apótema da base e h é a altura da pirâmide. 66 AZEVEDO FILHO, M. F. DE Prova. Sejam: V o vértice da pirâmide, e, O e l, respectivamente, o centro e o lado da base. Note que os triângulos formados por V, O e os vértices da base são congruentes entre si pelo caso L.A.L. de congruência de triângulos. Isso traz como conseqüência que as arestas laterais da pirâmide são congruentes entre si, logo, as faces laterais são triângulos isósceles congruentes entre si, todos com base medindo l. Assim, a área da superfície lateral da pirâmide é igual a n vezes a área de cada um desses triângulos, em que n é o número de lados da base. Já sabemos quanto mede a base de cada um deles: l. Resta calcularmos a altura. Esta é a hipotenusa de um triângulo retângulo cujos catetos são a al. tura h da pirâmide e o apótema da base da pirâmide, ou seja, Portanto, a soma das áreas das faces laterais da pirâmide regular é igual a , isto é, . Corolário 1 A área da superfície lateral de um cone circular reto é igual , em que r é o raio da base e h é a altura do cone, ou seja, rg a sendo g a medida de uma geratriz qualquer do cone. Prova. Seja n > 2 um inteiro. Consideremos um polígono regular de n lados inscrito na base e sejam pn e an, respectivamente, seu semi-perímetro e seu apótema. Então, a soma das áreas das faces laterais da pirâmide regular, cuja base é o polígono e cujo vértice é o vértice do cone dado, é igual a . A área da superfície lateral do cone circular reto é o limite desse . Desde que e quando , valor quando . decorre que a área da superfície lateral do cone é igual a Corolário 2 A área da superfície lateral de um tronco de pirâmide regular cuja altura é h, cujos semi-perímetros das bases são P e p, e, cujos apótemas das bases são A e a é igual a Prova. Digamos que P e A são, respectivamente, o semi-perímetro e o apótema da base maior. Seja h' a altura da pirâmide. Então, a razão de se, portanto, , melhança entre a base menor e a maior é , , e donde, Geometria Euclidiana Espacial 67 A pirâmide original está decomposta como soma do tronco mais uma pirâmide cuja base é a base menor do tronco e cuja altura é h' − h. Por conseguinte, a área da superfície lateral do tronco é igual a Corolário 3 A área da superfície lateral de um tronco de cone circular reto cuja altura é h e cujos raios das bases são R e r é igual a , isto é, (R + r)g em que g é a medida de uma geratriz qualquer do tronco. Prova. Seja n > 2 um inteiro. Consideremos um polígono regular de n lados inscrito na base maior, digamos, de raio R, e sejam Pn e An, respectivamente, seu semi-perímetro e seu apótema. Considere também o polígono regular de n lados inscrito na base de raio r correspondente ao anterior e sejam pn e an, respectivamente, seu semi-perímetro e seu apótema. Então, a área da superfície lateral do tronco da pirâmide cujas bases são esses polígonos vale . A área da superfície lateral do tronco do cone circular é o limite desse valor quando . quando , Desde que decorre que a área da superfície lateral do tronco do cone circular é igual a . 68 AZEVEDO FILHO, M. F. DE Teorema 94 A área da superfície de uma esfera de raio r é igual a 4 r2. Prova. Seja h > 0. Consideremos a esfera com o mesmo centro O da esfera dada e cujo raio é r + h, e, o sólido S que é o conjunto dos pontos da esfera de raio r + h não interiores à esfera de raio r, isto é, o conjunto dos pontos X tais que Iremos admitir que, para valores de h próximos de zero, é apro- ximado pelo volume do cilindro cuja área da base é a área da superfície da esfera de raio , que denotaremos por símbolos, isto quer dizer: donde, , e cuja altura é h. Em para pequenos valores de h, para valores de h próximos de zero. Assim sendo, temos: quando Desde que raio r, decorre o resultado. quando . é a área da superfície da esfera de Síntese do Capítulo Estudamos, inicialmente, congruência e semelhança de sólidos com abordagem de função. Demonstramos o importante teorema segundo o qual o volume de um paralelepípedo retangular é o produto de suas dimensões: largura, altura e comprimento. Este teorema, juntamente com o Princípio de Cavalieri, é a base das fórmulas do volume de outros sólidos. Em seguida, demonstramos as fórmulas dos volumes do cilindro, prisma, cone, tronco de cone, pirâmide e esfera, bem como a área da superfície de alguns desses sólidos. Geometria Euclidiana Espacial 69 Atividades de avaliação 1. Um metro cúbico contém quantos centímetros cúbicos? 2. Qual o número máximo de caixas cujas dimensões (exteriores) são 30cm, 20cm e 50cm que podem ser acomodadas em uma caixa cujas dimensões (interiores) são 2m, 3m e 5m. 3. Determine o volume e a área da superfície de uma esfera de raio igual a 2. 4. Em quantos por cento devemos aumentar a aresta de um cubo para que tenhamos um novo cubo com o dobro do volume do outro? 5. Em quantos por cento devemos aumentar a aresta de um cubo para que tenhamos um novo cubo com o dobro da área total do outro? 6. Determine o volume e a área total da superfície de um tronco de cone circular reto cujos raios das bases medem, respectivamente, 5cm e 1cm, e, cuja altura é de 3cm. 7. Calcule o volume do tronco de uma pirâmide regular e a área total da superfície desse tronco, cuja altura é 3, cujos semi-perímetros das bases maior e menor, respectivamente, são 45 e 9, e, cujos apótemas das bases maior e menor, respectivamente, são 5 e 1. 8. Demonstre que dentre os paralelepípedos retangulares de base quadrada com área total constante o de maior volume é o cubo. 9. Um prisma reto tem por base um triângulo retângulo cujos catetos medem 5cm e 12cm. A diagonal de sua maior face lateral forma um ângulo de 60o com o plano da base. Calcule sua área lateral. 10. Determine o volume e a área total de uma pirâmide regular de base quadrada sabendo que sua aresta lateral mede 5cm e suas faces laterais fazem um ângulo de 30o com a base. 11. Calcule, em função da aresta, o volume e a área da superfície de um tetraedro regular. 12.Demonstre que dentre os paralelepípedos retangulares com área total constante o de maior volume é o cubo. 13. Uma caixa fechada, em forma de um paralelepípedo retangular, tem as seguintes dimensões externas: x, y e z. Sabendo que sua espessura mede a, determine seu volume interno. 14. Uma lata fechada, em forma de cilindro circular reto, tem as seguintes dimensões externas: altura h e raio r. Sabendo que sua espessura mede a, determine seu volume interno. 70 AZEVEDO FILHO, M. F. DE 15. A geratriz de um cone circular reto forma com seu eixo um ângulo de 45o. Sabendo-se que o perímetro de sua seção meridiana mede 2cm, quanto vale a área total da superfície do cone? (Nota: o eixo de um cone circular reto é a reta que contém o vértice do cone e o centro de sua base, e, sua seção meridiana é a interseção de qualquer plano, que contém o eixo, com o cone.) 16. Um triedro tri-retângulo é cortado por um plano que intercepta as três arestas, formando um triângulo com lados medindo 8m, 10m e 12m. Determine o volume do sólido formado. 17. Um prisma reto de base hexagonal regular tem como altura o dobro da aresta da base. Qual a razão entre o volume deste prisma e o volume do cone circular reto nele inscrito? cm e cujo diâme18. Considere um cone circular reto cuja geratriz mede tro da base mede 2cm. Traçam-se n planos paralelos à base do cone que o seccionam determinando n + 1 cones, incluindo o original, de modo que a razão entre o volume do cone maior e do cone menor é 2. Os volumes desses cones formam uma progressão aritmética crescente cuja soma é igual a 2 . Determine o volume do tronco de cone determinado por dois planos consecutivos. Definição 95 Chama-se calota esférica as partes da superfície de uma esfera determinadas por um plano secante a ela. Definição 96 A região de uma esfera situada entre dois planos paralelos e secantes à ela é chamada de setor esférico e a superfície do setor esférico é denominada de zona esférica. Definição 97 A interseção de uma esfera com a região convexa determinada por um diedro cuja aresta contém o centro da esfera chama-se cunha esférica e a superfície da cunha denomina-se fuso esférico. 19. Expresse o volume de uma cunha esférica em função do raio r da esfera e da medida do ângulo diedral (em graus) que a determina, bem como a área do fuso esférico correspondente. 20. Um plano secante a uma esfera de raio r dista r – a de seu centro. Expresse a área da superfície da calota menor determinada pelo plano, em função de a e r, bem como o volume do sólido delimitado por essa calota e o plano. 21. Suponha que o centro de uma esfera de raio r pertence a um setor esférico determinado por dois planos que distam, respectivamente, a e b do centro. Expresse o volume do setor e área da zona esférica correspondente a esse setor em função de a, b e r. 22. Dois prismas têm mesma altura e bases regulares inscritas em círculos de Geometria Euclidiana Espacial 71 raios unitários com, respectivamente, 4 e 5 arestas. Demonstre que o que tem maior volume é aquele cuja base tem 5 arestas. 23. Dois prismas têm mesma altura e bases regulares inscritas em círculos de raios unitários com, respectivamente, n e n + 1 arestas. Demonstre que o que tem maior volume é aquele cuja base tem n + 1 arestas. 24. Um cone e um cilindro, ambos circulares retos, possuem o mesmo volume e bases com mesmo raio. Supondo que ambos são inscritíveis em uma esfera de raio r, determine a razão entre a altura do cone e r. 25. Considere uma esfera inscrita e tangente à base de um cone circular reto. Um cilindro está circunscrito à esfera de tal forma que uma de suas bases o volume do cone e o volume está apoiada na base do cone. Seja . do cilindro. Encontre o menor valor da constante k para o qual (Sugestão: considere o ângulo formado pelo diâmetro da base e a geratriz do cone em uma das extremidades deste diâmetro.) 26. Calcule o volume do tronco de uma pirâmide regular cuja altura é 3 e cujas respectivas áreas das bases são 3 e 12. e as respectivas áreas das bases de um tronco de cone 27. Sejam: e h sua altura. Mostre que seu volume obedece à seguinte fórmula: Capítulo Poliedros 4 Geometria Euclidiana Espacial 75 Objetivos: • Saber definir e classificar poliedro. • Conhecer os poliedros de Platão e os poliedros regulares. • Conhecer a Relação de Euler para poliedros convexos e saber como demonstrá-la. • Saber aplicar a Relação de Euler na resolução de problemas. • Conhecer a planificação dos principais poliedros. Os sólidos que estudamos até agora foram o cilindro, o cone e a esfera. Falta estudarmos mais um tipo importante de sólido: poliedro. Conforme veremos, são poliedros os prismas e as pirâmides. Assim, o estudo dos poliedros é uma extensão do estudo dos prismas e das pirâmides. 1. Definições O conceito de poliedro está para o espaço assim como o conceito de polígono está para o plano. Primeiramente, vamos recordar o conceito de polígono. Definição 98 Chama-se polígono a região de um plano delimitada por um número finito de segmentos de reta, contidos nesse plano, que satisfazem às seguintes condições: i) cada extremidade de qualquer segmento é extremidade de exatamente dois segmentos; ii) dois segmentos consecutivos quaisquer nunca são colineares; iii) dois segmentos não consecutivos quaisquer jamais se interceptam. Os segmentos são chamados de lados e suas extremidades de vértices do polígono. A reunião dos lados chama-se linha poligonal fechada, bordo ou para denotar o bordo de um fronteira do polígono. Adotaremos a notação polígono P. É o que veremos a seguir. 76 AZEVEDO FILHO, M. F. DE Nas figuras ao lado, o polígono da esquerda é convexo ao passo que o da direita é côncavo. Um polígono é convexo se satisfaz à seguinte condição: iv) fixado cada lado, os demais se encontram num mesmo semi-plano (em relação ao fixado). Definição 99 Dois polígonos P e Q serão chamados de consecutivos se . Definição 100 (Poliedro) Chama-se poliedro a região do espaço delimitada por um número finito de polígonos que satisfazem às seguintes condições: i) cada lado de qualquer polígono é lado de exatamente dois polígonos; ii) dois polígonos consecutivos quaisquer nunca são coplanares; iii) dois polígonos não consecutivos quaisquer jamais se interceptam. Os polígonos são chamados de faces, os lados das faces são chamados de arestas e os vértices das faces de vértices do poliedro. Chama-se diagonal do poliedro todo segmento de reta que une dois vértices não pertencentes a uma mesma aresta. A reunião das faces chama-se superfície, bordo ou fronteira do poliedro. Um poliedro é convexo se satisfaz à seguinte condição: iv) fixada cada face, as demais se encontram num mesmo semi-espaço (em relação à fixada). Nas figuras ao lado, o poliedro da esqueda é convexo ao passo que o da direita é côncavo. Seja P um poliedro com F faces que satisfaz à condição iv). Fixada a i-ésima face, as demais estão contidas num mesmo semi-espaço deteresse semi-espaço. Então, minado por esta face fixada. Denotemos por Chamaremos de poliedro convexo todo aquele que satisfaz à condição iv). Geometria Euclidiana Espacial 77 1.1 Representação Plana de um Poliedro Convexo Podemos representar um poliedro convexo num plano. Vejamos de que maneira. Consideremos o poliedro particular a seguir. O modo como procederemos nesse poliedro pode ser realizado num poliedro convexo qualquer. A idéia é a seguinte: consideremos apenos o ``esqueleto’’ do poliedro, isto é, somente as arestas e os vértices e imaginemos que as arestas podem tomar qualquer direção, ser esticadas ou encolhidas, como um elástico. Admitamos ainda que elas conservam suas formas de segmento de reta e que os vértices são ``nós’’ que não se desatam das arestas das quais são extremidades. Escolhamos qualquer uma das faces do poliedro, digamos, a face ABCD. Estiquemos suas arestas e, movimentando-as livremente, coloquemo-las num plano de tal modo que as demais arestas e vértices do poliedro fiquem em seu interior, decompondo esta face como soma das demais faces transformadas, conforme mostra a seguinte figura: Essa decomposição é possível dado que o poliedro é convexo. Enfim, temos aí uma representação plana do poliedro cujos vértices A, B, C, D, E, F e G correspondem, respectivamente, a A', B', C', D', E', F' e G'. Note que, nela, estão preservados o número de vértices, de arestas, de faces do poliedro, de arestas que partem de um mesmo vértice assim como a quantidade de arestas de uma mesma face. 78 AZEVEDO FILHO, M. F. DE Descubra segundo qual face. Chamaremos essa representação do poliedro de representação plana segundo a face ABCD. Veja, a seguir, exemplos de poliedros e à sua direita uma representação plana: 2. Relação de Euler Leonhard Euler, suíço, nasceu na cidade de Basiléia em 15 de abril de 1707 e morreu em 18 de setembro de 1783, em São Petersburgo. Muito precoce, aos vinte anos de idade, tornou-se membro associado da Academia de Ciências de São Petersburgo. Sua contribuição para a geometria analítica e para a trigonometria pode ser comparada à de Euclides para a geometria plana. É responsável por notações da Matemática utilizadas nos dias atuais tais como para ângulos de um e para constante neperiana, ∑ para somatório, para função, etc. triângulo, Figura 2 – Euler (1707-1783) Geometria Euclidiana Espacial 79 Um dos teoremas mais importantes da geometria euclidiana espacial é o que estabelece uma relação existente entre o número de vértices, arestas e faces de um poliedro convexo, conhecida por Relação de Euler. Ei-lo: Teorema 101 Se V, A e F são, respectivamente, o número de vértices, arestas e faces de um poliedro convexo, então Prova. Sejam P1, P2, ..., PF as faces do poliedro e n1, n2, ...,nF, respectivamente, o número de arestas de P1, P2, ..., PF . Consideremos a representação plana do poliedro segundo a face P1. Sejam A1, A2, ..., An1 os vértices correspondentes aos vértices de P1 nessa representação plana. Temos: n1 + n2 ... + nF = 2A, pois, de acordo com a definição de poliedro, cada aresta é aresta de exatamente duas faces e, portanto, na contagem n1 + n2 ... + nF computamos duas vezes o número de arestas. Agora vamos calcular o somatório de todos os ângulos internos de todos os polígonos da decomposição da face transformada A1 A2...An1. Faremos isso de dois modos e depois igualaremos os resultados. A primeiro modo será calculando-se a soma dos ângulos internos de cada polígono da decomposição e, em seguida, somar tudo. A face transformada está decomposta em F – 1 polígonos. Os números de lados desses polígonos são n2, n3, ...,nF. Por conseguinte, as respectivas somas de seus ângulos internos são 180o (n2 - 2) , 180o (n3 - 2) , ...,180o (nF - 2) . Logo, a soma de tudo é 180o [n2 + n3 + ... + nF - 2 (F - 1)] (I). A outra maneira de se calcular o somatório será feita calculando-se a soma dos ângulos internos de A1 A2 ...An1 e a este resultado somar os ângulos que ficam em torno dos vértices internos da decomposição de A1 A2 ...An1 . Note que a soma dos ângulos que ficam em torno de cada um desses vértices é igual a 360o . A quantidade desses vértices é V - n1, portanto, o somatório é igual a 180o (n1 - 2) + 360o (V -n1) (II). Igualando-se (I) a (II) e substituindo-se 80 AZEVEDO FILHO, M. F. DE n2 + n3 + ... + nF por 2A - n1 chega-se a 180o [2A - n1 - 2 (F - 1)] = 180o (n1 - 2) + 360o (V - n1), donde, segue-se que V - A + F = 2. Há uma importante classe de poliedros que recebe uma denominação em sua homenagem. Mosaico representando a Academia de Platão (Museu Arqueológico, Nápoles) Nesse teorema, a hipótese do poliedro ser convexo é essencial, ou seja, o teorema não é válido para um poliedro qualquer. Vamos dar exemplo de um poliedro (certamente côncavo) cujos números de vértices, arestas e faces não satisfazem à relação de Euler. Ei-lo: 3. Poliedros Regulares Platão, grego, foi um dos pensadores mais influentes de todos os tempos. Nasceu em Atenas por volta do ano 428 a.C. e lá morreu em 348. Foi o fundador de uma escola de filosofia chamada Academia situada em Atenas. Conheceu Euclides em Mégara com quem compartilhava das mesmas idéias. Veja a seguir dois exemplos. Figura 3 – Academia de Platão Nesse poliedro, temos: V = 12, A = 24 e F = 12, donde, V - A + F = 0. Um poliedro convexo chama-se poliedro de Platão se suas faces têm o mesmo número n de arestas e se de cada vértice partem o mesmo número m de arestas. Geometria Euclidiana Espacial 81 Sejam V, A e F, respectivamente, os números de vértices, arestas e faces de um poliedro de Platão. Pelo fato de suas faces terem o mesmo número n de arestas e cada aresta é aresta de exatamente duas faces, segue-se que nF = 2A; posto que de cada vértice partem o mesmo número m de arestas, decorre que mV = 2A e desde que o poliedro é convexo, então V - A + F = 2. Em suma, as seguintes relações são válidas para um poliedro de Platão: Expressando F e V em função de A, m e n e substituindo essas expres. Não podesões na relação de Euler, chegaremos à relação mos ter, simultaneamente, m ≥ 4 e n ≥ 4, pois se assim o fosse teríamos e , donde, e, por conseguinte, , o que é uma contradição. Portanto, m = 3 ou n = 3. , donde, Se m = 3, então seguinte, n < 6. Assim sendo, se m = 3, então n = 3, 4, ou 5. e, por con- Se n = 3, pelo mesmo argumento anterior, segue-se que m = 3, 4 ou 5. Em resumo, as possibilidades para m e n, respectivamente, são: 3 e 3, 3 e 4, 3 e 5, 4 e 3, e, 5 e 3. Para cada uma dessas possibilidades, podemos determi, nar os respectivos valores de A, V e F utilizando as relações mV = 2A e nF = 2A. m 3 3 3 4 5 n 3 4 5 3 3 A 6 12 30 12 30 V 4 8 20 6 12 F 4 6 12 8 20 Denominação tetraedro hexaedro dodecaedro octaedro icosaedro Note que essas denominaões são quanto ao número de faces. Observe ainda que as faces são triângulos, quadriláteros ou pentágonos. A análise que acabamos de fazer nos permite enunciar o A tabela a seguir reúne esses resultados. 82 AZEVEDO FILHO, M. F. DE As linhas cheias indicam recortes, as pontilhadas dobraduras e as partes sombreadas colagem. Teorema 102 Quanto ao número de faces, há, no máximo, cinco poliedros de Platão. Definição 103 Um poliedro de Platão chama-se regular se todas suas faces são polígonos regulares. Veja a seguir os cinco poliedros regulares existentes, quanto ao número de faces. Informações mais detalhadas sobre os poliedros de Platão se encontram na tabela anterior. Em seguida, apresentamos planificações dos poliedros regulares a fim de se construí-los com folha de cartolina ou outro material similar. Geometria Euclidiana Espacial 83 84 AZEVEDO FILHO, M. F. DE Geometria Euclidiana Espacial 85 Síntese do Capítulo No início, fizemos uma revisão da definição de polígono para logo em seguida darmos a definição de poliedro. Tratamos da planificação de um poliedro convexo, segundo uma de suas faces. Apresentamos e demonstramos o teorema que estabelece a chamada Relação de Euler para poliedros convexos. Como aplicação desta relação, demonstramos que só existem cinco poliedros de Platão, quanto ao número de faces. Por fim, apresentamos as planificações dos poliedros regulares com a finalidade de confeccioná-los utilizando cartolina. Atividades de avaliação 1. Expresse o número de arestas A de uma pirâmide, em função do número n de lados de sua base. 2. Expresse o número de arestas A de um prisma, em função do número n de lados de sua base. 3. Mostre que dado um inteiro n ≥ 4, existe um poliedro convexo cujo número de faces é n. 4. Calcule o número de arestas e de vértices de um poliedro convexo com oito faces, das quais cinco são triangulares e três são pentagonais. 5. Calcule o número de arestas e de vértices de um poliedro convexo com onze faces, das quais sete são triangulares, três são pentagonais e uma é hexagonal. 6. Calcule o número de arestas e de vértices de um poliedro convexo com doze faces, todas pentagonais. 7. Calcule o número de arestas e de vértices de um poliedro convexo com onze faces, das quais nove são quadrangulares e duas são pentagonais. 8. Desenhe, para cada poliedro regular, uma planificação segundo uma de suas faces. 9. Determine os números de vértices, arestas e faces de um poliedro convexo sabendo-se que cada vértice é vértice de exatamente dois hexágonos regulares e um quadrado. Tente desenhar uma planificação para se construir, em cartolina, este poliedro. (Algumas abelhas guardam o mel em reservatórios com esse formato. Assim como cubos de mesma aresta têm a propriedade de serem empilhados sem deixar espaços vazios, esses poliedros têm esta 86 AZEVEDO FILHO, M. F. DE propriedade com uma vantagem a mais: dentre os poliedros convexos empilháveis com uma mesma área de superfície ele é o de volume máximo.) 10. Determine os números de vértices, arestas e faces de um poliedro convexo sabendo-se que cada vértice é vértice de exatamente dois hexágonos e um pentágono, regulares. Você seria capaz de desenhar uma planificação para se construir, em cartolina, um tal poliedro? (A bola de futebol usada na Copa de 1970 tinha esse formato. Esse poliedro foi descoberto por Arquimedes.) 11. Determine os números de vértices, arestas e faces de um poliedro convexo sabendo-se que cada vértice é vértice de exatamente dois pentágonos e um hexágono. 12. Um poliedro convexo de 16 arestas é formado por faces triangulares e quadrangulares. Seccionado-o por um plano convenientemente escolhido, dele se destaca um novo poliedro convexo, que possui apenas faces quadrangulares. Este novo poliedro possui um vértice a menos que o original e uma face a mais que o número de faces quadrangulares do original. Determine o número de faces e o número de vértices do poliedro original. 13. Mostre que a soma dos ângulos de todas as faces de um poliedro convexo é igual a 360o (V - 2), em que V é o número de vértices do poliedro. 14. Mostre que se um poliedro convexo tem 10 arestas, então seu número de faces e seu número de vértices são iguais a 6. 15. Determine os poliedros convexos com 10 arestas quanto ao número de arestas partindo de seus vértices. Desenhe-os. 16. Os itens a seguir, deste exercício, têm como objetivo garantir a existência dos octaedros regulares e também estabelecer algumas de suas propriedades. a) Mostre que existe uma pirâmide regular cujas faces laterais são triângulos equiláteros e cuja base é um quadrado. Determine sua altura h em função de sua aresta a. b) Mostre que existe um octaedro regular. c) Há um ponto no octaedro regular que é equidistante de seus vértices e de suas faces, chamado de centro do mesmo, que é centro comum das esferas inscrita e circunscrita a ele. Calcule, em função de sua aresta a, os raios R e r, respectivamente, das esferas circunscrita e inscrita nele, bem como seus ângulos diedrais. d) Calcule a área ção de a. da superfície e o volume do octaedro regular em fun- e) Mostre que os centros das faces do octaedro regular são vértices de um cubo. Geometria Euclidiana Espacial 87 17. Mostre que os centros das faces de um cubo são vértices de um octaedro regular. 18. Um cubo tem aresta a. Determine, em função de a, a razão entre o volume e a área total da superfície do poliedro cujos vértices são os centros das faces do cubo. 19. Um octaedro regular é inscrito num cubo, que está inscrito numa esfera, a qual está inscrita num tetraedro regular de aresta a. Em função de a, determine a aresta do octaedro. 20. Mostre que o poliedro referido no exercício 8 pode ser construído a partir de um octaedro regular seccionando-se as faces em torno de cada um de seus vértices com um plano que determina em cada uma delas um triângulo semelhante cuja razão de semelhança é igual a um terço. Este poliedro tem a denominação de octaedro regular truncado. 21. Há um ponto no octaedro regular truncado que é equidistante de seus vértices, chamado de circuncentro do mesmo, que é o centro da esfera circunscrita a ele. Calcule, em função de sua aresta a, o raio R da esfera circunscrita bem como seus ângulos diedrais. Calcule também a área de sua superfície e seu volume em função de a. 22. Os itens a seguir, deste exercício, têm como objetivo garantir a existência dos icosaedros e dodecaedros regulares, e, também estabelecer algumas de suas propriedades. a) Mostre que existe uma pirâmide regular cujas faces laterais são triângulos equiláteros e cuja base é um pentágono. Determine sua altura h em função de sua aresta a. b) Mostre que existe um icosaedro regular. c) Mostre que há um ponto no icosaedro regular que é equidistante de seus vértices e de suas faces, chamado de centro do mesmo, que é centro comum das esferas inscrita e circunscrita a ele. Calcule, em função de sua aresta a, os raios R e r, respectivamente, das esferas circunscrita e inscrita nele, bem como seus ângulos diedrais. d) Calcule a área função de a. da superfície e o volume do icosaedro regular em e) Mostre que os centros das faces do icosaedro regular são vértices de um dodecaedro regular (conseqüentemente, existe um dodecaedro regular). f) Mostre que existe um ponto no dodecaedro regular que é equidistante de seus vértices e de suas faces, chamado de centro do mesmo, que é centro comum das esferas inscrita e circunscrita a ele. Calcule, em função de sua aresta, os raios, respectivamente, das esferas circunscrita e inscrita nele, bem como seus ângulos diedrais. 88 AZEVEDO FILHO, M. F. DE g) Calcule a área da superfície e o volume do dodecaedro regular em função de sua aresta. h) Calcule a área da superfície e o volume do icosaedro e do dodecaedro, regulares, inscritos na esfera de raio unitário, e, compare os resultados. 23. Mostre que os centros das faces de um dodecaedro regular são vértices de um icosaedro regular. 24. Mostre que o poliedro referido no exercício 9 pode ser construído a partir de um icosaedro regular seccionando-se as faces em torno de cada um de seus vértices com um plano que determina em cada uma delas um triângulo semelhante cuja razão de semelhança é igual a um terço. Este poliedro tem a denominação de icosaedro regular truncado. 25. Há um ponto no icosaedro regular truncado que é equidistante de seus vértices, chamado de circuncentro do mesmo, que é o centro da esfera circunscrita a ele. Calcule, em função de sua aresta a, o raio R da esfera circunscrita bem como seus ângulos diedrais. Calcule também a área de sua superfície e seu volume em função de a. Respostas Capítulo 1 3) As extremidades de rês pernas determinam o plano do piso. Quanto à extremidade a quarta perna, esta pode ou não pertencer a esse plano. 4) Nem sempre. 5) Não. 19) Capítulo 2 1) 2) 120o. 3) 5. 4) e a soma dos ângulos de todas as faces é 15120 . o 5) 6) . Geometria Euclidiana Espacial 89 7) 9) a) ; b) a, em que a é a aresta da base; c) o cosseno dos ângulos da base é , logo, esses ; o cosseno do ângulo ângulos medem, aproximadamente, , logo, esse ângulo mede, aproximaoposto à base é o damente, 63 24'16"; d) , portanto, o ângulo mede, aproximadamente, 112 25' 39" . o 10) . 11) . 15) Esfera tendo como diâmetro, menos A e B. 19) a) d) ângulo diedral: arccos 21) 22) 23) 10/3. 24) Capítulo 3 1) 106cm3 = milhão de cm3. 2) 1000. 3) e 4) 5) 6) 7) 9) 10) e . 90 AZEVEDO FILHO, M. F. DE 11) 13) 14) 15) 16) 17) 18) 19) 20) 21) 24) 6/5. 25) 4/3. 26) 21. Capítulo 4 1) A= 2n. 2) A = 3n. 4) V = 9 e A = 15. 5) V = 12 e A = 21 . 6) V = 20 e A = 30 . 7) V = 14e A = 23 . 8) Geometria Euclidiana Espacial 91 9) V = 24, A = 36 e F = 14. 10) V = 60, A = 90 e F = 32. 11) V = 30, A = 45 e F = 17. 92 AZEVEDO FILHO, M. F. DE 12) O número de faces e o número de vértices do poliedro original são iguais a 9. 15) São dois. Primeiro: de 5 vértices partem 3 arestas e de um vértice partem 5. Segundo: de 4 vértices partem 3 arestas e de 2 vértices partem 4 arestas. 16) a) c) e os ângulos diedrais são iguais ao arccos d) 18) 19) a/6. 21) faces hexagonais é igual ao arccos o ângulo entre duas 109 28' 16" e o ângulo entre o uma face quadrada e uma hexagonal é o arccos 22) c) 0,9511a, 0,7558a e os ân- gulos diedrais medem arccos d) f) 138o 11' 23" ; 8,6603a2 e 2,1817a3 ; 1,4013ad, 1,1135ad e os 116o 33' 54"; ângulos diedrais medem arccos g) h) 125o 15' 52". e Geometria Euclidiana Espacial 93 25) , o ângulo entre duas faces hexagonais mede, aproximadamente, e o ângulo entre uma face pentagonal e uma hexagonal mede, aproximadamente, Referências BARBOSA, João Lucas Marques. Geometria Euclidiana Plana. Sociedade Brasileira de Matemática, Rio de Janeiro, 1985. BARSA, Nova Enciclopédia. Enciclopædia Britannica do Brasil. Publicações LTDA., Rio de Janeiro, 1998. BLUMENTHAL, Leonard M. Geometria Axiomatica. Aguilar, Madrid, 1965. BOYER, Carl B. História da Matemática. Editora Edgard Blücher. LTDA., São Paulo, 1974. CARVALHO, Paulo César Pinto. Introdução à Geometria Espacial. SBM, Rio de Janeiro, 1993. COXETER, H. S. M. Introduction to Geometry. John Wiley & Sons, Inc., New York, 1965. COXETER, H. S. M. e GREITZER, S. L. Geometry Revisited. Random House, New York, 1967. IEZZI, Gelson - DOLCE, Osvaldo e outros. Matemática vol. 2. Atual Editora LTDA., São Paulo, 1976. LIMA, Elon Lages. Áreas e Volumes. SBM, Rio de Janeiro, 1979. Sobre o autor Manoel Ferreira de Azevedo Filho: possui mestrado em Matemática pela Universidade Federal do Ceará (1981). Atualmente é professor aposentado da Universidade Federal do Ceará, professor de ensino superior da Faculdade Farias Brito e professor adjunto da Universidade Estadual do Ceará. A não ser que indicado ao contrário a obra Geometria Euclidiana Espacial, disponível em: http://educapes.capes. gov.br, está licenciada com uma licença Creative Commons Atribuição-Compartilha Igual 4.0 Internacional (CC BY-SA 4.0). Mais informações em: <http://creativecommons.org/licenses/by-sa/4.0/deed.pt_BR. Qualquer parte ou a totalidade do conteúdo desta publicação pode ser reproduzida ou compartilhada. Obra sem fins lucrativos e com distribuição gratuita. O conteúdo do livro publicado é de inteira responsabilidade de seus autores, não representando a posição oficial da EdUECE. Matemática Geometria Euclidiana Espacial Universidade Estadual do Ceará - Universidade Aberta do Brasil F iel a sua missão de interiorizar o ensino superior no estado Ceará, a UECE, como uma instituição que participa do Sistema Universidade Aberta do Brasil, vem ampliando a oferta de cursos de graduação e pós-graduação na modalidade de educação a distância, e gerando experiências e possibilidades inovadoras com uso das novas plataformas tecnológicas decorrentes da popularização da internet, funcionamento do cinturão digital e massificação dos computadores pessoais. Comprometida com a formação de professores em todos os níveis e a qualificação dos servidores públicos para bem servir ao Estado, os cursos da UAB/UECE atendem aos padrões de qualidade estabelecidos pelos normativos legais do Governo Federal e se articulam com as demandas de desenvolvimento das regiões do Ceará. Geometria Euclidiana Espacial Matemática Manoel Ferreira de Azevedo Filho Geografia 12 9 3 História Educação Física Química Ciências Biológicas Artes Plásticas Computação Física Matemática Pedagogia