Enviado por
common.user5445
EXPERIMENTO DE MILLIKAN-PARCIAL

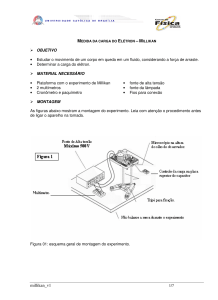
UNIVERSIDADE ESTADUAL DE SANTA CRUZ DEPARTAMENDO DE CIÊNCIA EXATAS E TECNOLÓGICAS FÍSICA LICENCIATURA O EXPERIMENTO DE MILLIKAN: A queda da gota de óleo. RONILDO LOPES D’ AJUDA (201610656), ILHÉUS – BAHIA 2019 RONILDO LOPES D’ AJUDA (201610656), O EXPERIMENTO DE MILLIKAN: A queda da gota de óleo. Relatório apresentado como parte dos critérios de avaliação da disciplina CET 187 – Laboratório de Física Moderna. Turma T01 / P01. Professor: Dr. Fernando Remigio Tamariz Luna ILHÉUS – BAHIA 2019 SUMÁRIO 1 INTRODUÇÃO 4 2 REFERENCIAL TEÓRICO 5 3 O EXPERIMENTO 10 4 RESULTADOS E DISCUSSÃO 12 REFERÊNCIAS 13 4 1 INTRODUÇÃO Há uns100 anos, vários cientistas brilhantes dedicaram suas vidas ao minucioso empe- nho de medir constantes relacionadas a fenômenos físicos, como, por exemplo: a carga do elétron, velocidade da luz, constantes energéticas (Planck), entre outras, como forma de permitir que esses dados propiciassem uma forte base de apoio para as novas descobertas nas áreas da física e da química, entre elas o efeito fotoelétrico, explicado por Albert Einstein em 1905, e a Mecânica Quântica. Foi neste cenário científico que surgiu um brilhante físico norteamericano, chamado Robert Millikan (1868-1953), empenhado em encontrar o valor da “carga elementar” do elétron. Nesta época, a física vivia um momento único, com a descoberta dos raios X, da radiatividade, do elétron e do quantum de radiação, que descortinava perspectivas de cuja existência nem se podia suspeitar, antes. Isso fazia a mente de Millikan borbulhar e o impulsionava contra toda e qualquer dificuldade [1]. Millikan iniciou pesquisas para determinar a quantidade de carga elétrica num elétron a partir de 1906. Para tanto, analisou o comportamento que gotículas de água eletricamente carregadas manifestavam quando submetidas a influências de forças no interior de uma câmara fechada: a da viscosidade, gravidade e a elétrica. Deparou-se, então, com um problema: a água se evapora [1]! Sendo assim, em 1909, R. Millikan relatou um método confiável para medir cargas iônicas. Consiste em observar o movimento de pequenas gotículas de óleo sob a influência de um campo elétrico [2]. A experiência de Millikan está enquadrada entre as dez mais famosas na área de Ciências Físicas, pelo menos é o que indica o resultado de uma enquete realizada entre seus leitores da revista Physics World sobre o mais belo experimento da física, na edição de setembro de 2002. O primeiro grande artigo de Millikan, sobre a gota de óleo eletrizada foi submetido à Philosophical Magazine em outubro de 1909, enquanto que o segundo foi publicado na Science, em 1910, portanto há cem anos [1]. O experimento é bastante simples e consiste em medir o tempo de deslocamento de gotículas de óleo, previamente eletrizadas, em três situações distintas: sujeitas apenas à influência da força da gravidade, e sob a ação de um campo elétrico externo a favor e contra a força da gravidade. Nesse experimento Millikan focou nos seguintes objetivos: Determinar experimentalmente o valor da carga elementar do elétron e; verificar o caráter discreto da magnitude da carga elétrica. 5 2 REFERENCIAL TEÓRICO O atrito experimentado pelas gotículas de óleo, ao longo do trajeto reservatório-borrifador-capilar-capacitor, faz com que estas fiquem naturalmente eletrizadas com cargas de elétrons 𝑒, assim, os campos convencionais lhes conferem velocidades que imitam o isolamento de uma gota e a observação contínua por um período de tempo considerável; mais distante. a massa da gota de óleo permanece quase constante (ocorre uma leve evaporação), atrevendo esses longos tempos de observação. Em princípio, se medirmos a força devida ao campo elétrico 𝐸⃗ , 𝑉 𝐹𝑒 = 𝑞𝐸⃗ = 𝑛𝑒𝐸⃗ = 𝑞 ( ) 𝑠̂ 𝑠 (1) em que 𝑞 é a carga da gota de óleo, 𝑉 é a diferença de potencial entre as placa e S é a distância entre as mesmas. Nós podemos obter 𝑛𝑒; repetindo essa medição para várias quedas (ou as mesmas), mas com valores diferentes do número inteiro 𝑛, podemos extrair a carga do elétron 𝑒. A força elétrica pode ser medida por um método nulo, ou seja, equilibrando a queda da força gravitacional ou, como será descrito aqui, observando o movimento da queda sob a influência de ambas as forças. Gotas de óleo no ar, atuadas por uma força constante 𝐹, logo atingem uma velocidade terminal dada pela lei de Stokes, 𝐹𝑎𝑡 = −6𝜋𝑎𝜂𝑣 (2) onde 𝑎 é o raio da gotícula (presumida esférica), 𝜂 a viscosidade do ar e, 𝑣 a velocidade terminal. Para obter o raio da gota (necessário na Eq. 2), observamos a queda livre da gota; a força gravitacional é 4 𝐹𝑔 = 𝜋𝑎3 𝜌𝑔 3 (3) onde ρ é diferença entre a densidade do ar ρar e a densidade do óleo ρóleo e "𝑔", a aceleração da gravidade. Esquematicamente, como mostrado na Fig.1, o aparelho consiste em duas placas paralelas que podem ser carregadas alternativamente a um potencial constante + V, - V ou 0. A queda é observada (com um telescópio) e o tempo que o óleo leva para viajar através de uma distância 𝑑 é medido. Chamaremos de 𝐹𝑑 a força resultante de descida em uma queda cujo campo elétrico 𝐸⃗ ativado atua na mesma direção e sentido de 𝑔 (o tempo de descida é 𝑡𝑑 , e a força elétrica 𝐹𝑒𝑑 auxilia a gravidade), 𝐹𝑠 força resultante de subida cujo campo elétrico 𝐸⃗ ativado atua na mesma direção e sentido contrário de 𝑔 (o tempo é 𝑡𝑠 , e a força elétrica 6 𝐹𝑒𝑠 age contra a gravidade) e 𝐹0 a força resultante de queda com campo elétrico desativado (o tempo é 𝑡0 , e a força elétrica é nula). Então Na situação em que a gota de óleo atinge a velocidade terminal temos: |𝐹0 | = |𝐹𝑔 | − |⃗⃗𝐹𝑎𝑡 | = 0 |𝐹𝑑 | = |𝐹𝑔 | + | 𝐹𝑒𝑑 | − |⃗⃗𝐹𝑎𝑡 | = 0 |𝐹𝑠 | = |𝐹𝑒𝑑 | − (| 𝐹𝑔 | + |⃗⃗𝐹𝑎𝑡 |) = 0. . Substituindo as força pela expressão correspondente a cada uma delas, segue que: 𝐹0 = 4 3 𝜋𝑎 𝜌𝑔 = 6𝜋𝑎𝜂𝑑(1⁄𝑡0 ) 3 (4𝑎) 4 (𝑛) 𝐹𝑑 = 𝑞(𝑉 ⁄𝑠) + 𝜋𝑎3 𝜌𝑔 = 6𝜋𝑎𝜂𝑑(1⁄𝑡𝑑 ) 3 (4𝑏) 4 (𝑛) 𝐹𝑠 = 𝑞(𝑉 ⁄𝑠) − 𝜋𝑎3 𝜌𝑔 = 6𝜋𝑎𝜂𝑑(1⁄𝑡𝑠 ). 3 (4𝑐) Como a distancia 𝑑 e o tempo 𝑡 são medidos, podemos obter a velocidades seguintes: 𝑣0 = 𝑑 𝑑 𝑑 ; 𝑣𝑑 = (𝑛) ; 𝑣𝑑 = (𝑛) 𝑡0 𝑡𝑑 𝑡𝑠 𝑉=0 𝑝𝑙𝑎𝑐𝑎 𝑚𝑒𝑡á𝑙𝑖𝑐𝑎 𝑠𝑢𝑝𝑒𝑟𝑖𝑜𝑟 (𝑛𝑒𝑢𝑡𝑟𝑎) 𝐹𝑎𝑡 𝐸⃗ = 0 𝑒− 𝑣𝑜 𝐹𝑔 𝑝𝑙𝑎𝑐𝑎 𝑚𝑒𝑡á𝑙𝑖𝑐𝑎 𝑖𝑛𝑓𝑒𝑟𝑖𝑜𝑟 (𝑛𝑒𝑢𝑡𝑟𝑎) FIGURA 1a – Força em uma gota de óleo sem a presença do campo elétrico. 𝑆 7 𝑉 = −𝑉 𝑝𝑙𝑎𝑐𝑎 𝑚𝑒𝑡á𝑙𝑖𝑐𝑎 𝑠𝑢𝑝𝑒𝑟𝑖𝑜𝑟 (𝑛𝑒𝑔𝑎𝑡𝑖𝑣𝑎) 𝐹𝑎𝑡 𝑒− 𝐸⃗ 𝐹𝑔 𝑆 𝑣𝑑 𝐹𝑒𝑑 𝑝𝑙𝑎𝑐𝑎 𝑚𝑒𝑡á𝑙𝑖𝑐𝑎 𝑖𝑛𝑓𝑒𝑟𝑖𝑜𝑟 (𝑝𝑜𝑠𝑖𝑡𝑖𝑣𝑎) FIGURA 1b – Força em uma gota de óleo carregada entre as placas com o campo elétrico na mesma direção e sentido contrário ao campo gravitacional. 𝑉 = +𝑉 𝑝𝑙𝑎𝑐𝑎 𝑚𝑒𝑡á𝑙𝑖𝑐𝑎 𝑠𝑢𝑝𝑒𝑟𝑖𝑜𝑟 (𝑝𝑜𝑠𝑖𝑡𝑖𝑣𝑎) 𝐹𝑒𝑠 𝑒− 𝐸⃗ 𝐹𝑔 𝑣𝑠 𝑆 𝐹𝑎𝑡 𝑝𝑙𝑎𝑐𝑎 𝑚𝑒𝑡á𝑙𝑖𝑐𝑎 𝑖𝑛𝑓𝑒𝑟𝑖𝑜𝑟 (𝑛𝑒𝑔𝑎𝑡𝑖𝑣𝑎) FIGURA 1c – Força em uma gota de óleo carregada entre as placas com o campo elétrico na mesma direção e sentido do campo gravitacional. Podemos obter uma expressão para carga 𝑞 somando as equações (4b) e 4(c), 𝑉 2𝑞 ( ) = 6𝜋𝑎𝜂(𝑣𝑑 + 𝑣𝑠 ) 𝑠 𝑞= 3𝜋𝑎𝜂𝑠 (𝑣𝑑 + 𝑣𝑠 ) 𝑉 (5) Note que a carga da partícula depende de seu raio 𝑎, logo para determinar a carga de uma gotícula utilizamos a equação (4a) e obtemos uma expressão para o raio a da gotícula. 8 Isolando e 𝑎 e fazendo utilizando a velocidade de queda 𝑣0 com o campo desativado. Temos, 𝑎2 = 9 𝜂𝑣0 . 2 𝜌𝑔 (6) quando o diâmetro da gota é comparável ao caminho livre médio no ar, a viscosidade 𝜂 deve ser corrigida tanto pela temperatura quanto pela pressão local, 𝑏 −1 𝜂(𝑇, 𝑃) = 𝜂0 (𝑇) [1 + ] , 𝑎𝑃 (7) onde P e T é a pressão e a temperatura local, respectivamente, 𝜂0 (𝑇) é a viscosidade do ar em função de 𝑇 (Fig. 2), 𝑏 = 6,17𝑥10−6 𝑃𝑎. 𝑚, 𝑃 é a pressão do ar em centímetros de mercúrio e 𝑎 é o raio de queda em metros (da ordem de 10−6 𝑚) FIGURA 2 – Viscosidade do ar seco como uma função da temperatura. Os pontos de dados são retirados de D. Pnueli e C. Gutfinger. Mecânica dos Fluidos, Cambridge Univ. Pressione. Cambridge UK. 1992. Tabela B-1. Esses pontos são ajustados a um polinômio de segunda ordem para interpolar à temperatura no laboratório. 9 sendo assim, podemos reescrever a expressão para 𝑎, substituindo o valor de 𝜂 da equação (7) na equação (6). A equação resultante fica assim 𝑏 𝑏 2 9 𝜂0 𝑣0 𝑎=− + √( ) + . 2𝑃 2𝑃 2 𝜌𝑔 (8) Substituindo valor de 𝑎 dado pela equação (8) na equação (5), temos 𝑞= 3𝜋𝜂𝑠 𝑏 𝑏 2 9 𝜂0 𝑣0 [− + √( ) + ] (𝑣𝑑 + 𝑣𝑠 ) . 𝑉 2𝑃 2𝑃 2 𝜌𝑔 (9) Um método conveniente de análise é escrever a Eq. (4b) e (4c) como 1 (𝑛) 𝑡𝑑𝑠 𝐴= = 𝐴𝑛𝑑𝑠 − 𝐵 (10𝑎) 𝑉𝑒 6𝑠𝜋𝑎𝜂𝑑 (10𝑏) 1 = −𝐵 𝑡0 𝐵= 2 𝑎2 (𝜌 − 𝜎)𝑔 9 𝜂𝑑 (10𝑐) (10𝑑) para que A e B possam ser facilmente determinados. (𝑛) De fato, um gráfico de 1⁄𝑡𝑑𝑠 contra 𝑛 revela a relação linear e o fato de que apenas valores inteiros de 𝑛 aparecem, provando que a queda adquiriu uma, duas, três ou mais cargas elétricas de valor 𝑒 e nunca uma fração desse valor. Assim, temos evidências claras de que a carga iônica captada pelas gotas de óleo é quantizada. Além disso, o valor absoluto dessa carga elétrica mínima está de acordo com a medição inferida da carga transportada pelos elétrons atômicos e, portanto, é aceito como o valor mais preciso da carga do elétron. 10 3 O EXPERIMENTO O aparelho usado neste laboratório (Fig. 3) consiste em duas placas de latão paralelas com 1 cm de espessura e aproximadamente 2 cm de diâmetro, colocadas em um cilindro de lucita separado por três espaçadores de cerâmica com 4,7 mm de comprimento. Este conjunto é, por sua vez, encerrado em um compartimento cilíndrico de latão com provisões para conexões elétricas e contendo duas janelas, uma para iluminação das gotas e outra para observação. A placa superior possui um pequeno orifício no centro para a admissão de gotas de óleo, que são produzidas pulverizando óleo com um atomizador comum. Para carregar as placas, uma fonte de alimentação de 500 𝑉 𝐷𝐶 e um interruptor de inversão usado, as placas são derivadas por um resistor de 50 𝑀Ω para impedir que permaneçam carregadas quando a chave está aberta. Para observações, é utilizado um microscópio de 10 cm de distância focal (Cenco 72925), enquanto a iluminação é fornecida por uma lâmpada Mazda 1017-W e lente de condensação. Para evitar correntes de convecção no interior do aparelho, um filtro de absorção de calor (absorção de infravermelho da Corning) é colocado no feixe de iluminação. As placas devem ser perpendiculares ao campo gravitacional por meio dos três parafusos de nivelamento na base do aparelho e um nível colocado na placa superior. Sendo um erro cosseno, o desvio introduzido por um deslocamento angular do componente gravitacional da perpendicular em 8º é de 1%. Um valor para o espaçamento "s" entre as placas pode ser obtido usando o micrômetro de estágio. O micrômetro deve ser focado em um fio inserido no orifício de óleo no centro da placa superior, e a mira do micrômetro deve ser movida ao longo do comprimento do fio. Várias medidas devem ser tomadas e seus resultados, em média. FIGURA 3 - Esquema do aparelho de Millikan utilizado no experimento de gota de óleo. 11 As velocidades são determinadas medindo com um cronômetro o tempo necessário para que a gota cubra um número especificado de divisões da escala do microscópio. Deve-se tomar cuidado para evitar correntes de ar e vibrações nas proximidades do aparelho; por esse motivo e por causa do movimento browniano, a gota pode vagar ou ser deslocada para fora do campo do microscópio. Pode ser necessário reposicionar o microscópio entre as medições em uma única gota. Além disso, a queda deve ser mantida em foco para evitar erros de paralaxe. Tanto o microscópio quanto a fonte de luz podem ser ajustados visualizando um pequeno fio inserido no orifício de óleo. A luz deve ser ajustada para que o ponto focal fique um pouco parado ou atrás do fio e o fio fique mais ou menos uniformemente iluminado. Para iluminar a balança, uma pequena luz é colocada ao lado da fenda na extremidade da ocular do microscópio. A distância real à qual uma divisão de escala corresponde pode ser encontrada usando uma lâmina de microscópio na qual uma escala milimétrica subdividida foi arranhada. [3] O foco da ocular do microscópio não deve ser alterado durante uma corrida, pois o movimento da ocular altera a distância efetiva da balança. (Para trazer a gota de volta ao foco, todo o microscópio deve ser movido.) É importante poupar a quantidade de óleo pulverizado na câmara. Além de absorver o interior mais rapidamente, grandes quantidades criam tantas partículas no campo do microscópio que, sem fadiga ocular excessiva, é praticamente impossível destacar e seguir uma única gota. Sob a influência da gravidade, as gotas caem em várias velocidades limitantes. Se as placas estiverem carregadas, algumas gotas cairão mais rapidamente, enquanto outras reverterão sua direção de movimento, pois no processo de pulverização algumas gotas ficam carregadas positivamente e outras carregadas negativamente. Concentrando-se em uma gota, a qual pode ser controlada pelo campo e manipulando o sinal do campo elétrico para que essa gota em particular seja retida, é possível remover todas as outras gotas do campo. A velocidade limite é alcançada muito rapidamente e a medição deve ser iniciada perto da parte superior ou inferior da placa. A medição deve ser concluída antes que a gota atinja um ponto no seu percurso em que a aplicação do potencial reverso seja insuficiente para evitar que a gota seja "consumida". A densidade no ar do óleo utilizado foi de 0,883 ± 0,003 𝑔/𝑐𝑚3. É desejável realizar medições no menor tempo possível, pois, como mencionado anteriormente, a massa da gota muda por evaporação. Também é importante fazer medições com o maior número de cargas diferentes na mesma ou em diferentes gotas possíveis. Assim, após quatro ou cinco medições de 𝑡𝑑 , 𝑡𝑠 e 𝑡0 , terem sido tomadas, a carga na gota deve ser alterada, isso é conseguido trazendo para perto de uma das janelas uma fonte radioativa (10 a 100 µCi de Co60 farão). A gota deve ser trazida para perto da placa superior e deixada cair com o campo; no seu caminho, varrerá alguns íons criados pela fonte. Isso pode ser verificado ativando o campo ocasionalmente para ver se o valor foi alterado; raramente uma gota adquire qualquer 12 valor quando o campo está ativado. A tensão da fonte de alimentação deve ser verificada com um multímetro digital a 1% (DMM); a calibração do microscópio deve ser verificada antes e depois das medições. 4 RESULTADOS E DISCUSSÃO O valor da carga do elétron só foi possível através da análise estatística de um número suficientemente grande de dados experimentais. Millikan mediu a carga de 10.000 gotas de óleo e verificou que todos esses valores eram múltiplos inteiros de certo número, encontrando assim a “carga elementar (e)”, ou menor carga possível (carga do elétron). O grande número de medidas foi escolhido com base no cálculo do desvio padrão. Como o erro em uma medida, estatisticamente, é um número proporcional à raiz quadrada do número de medições (Erro ∝ n), 10.000 medidas implicam em um erro da ordem de 1%. Foi um trabalho extremamente meticuloso. A partir do conhecimento dos tempos de subida e de queda da tensão aplicada entre as placas foi possível estimar o número de cargas elementares contidas na gota. Os valores de 𝑎 e 𝑞 foram calculados, utilizando todos os parâmetros, cuidadosamente determinados e com os respectivos erros avaliados. As condições da pressão e temperatura foram medidas no início e no final da experiência. Com algumas medidas e o tratamento matemático utilizado por Millikan o valor para a carga do elétron encontrada foi de 1,59 x 10-19 C. A descoberta feita pelo americano Robert Andrews Millikan do valor da carga do elétron, carga elementar, como é referida, revolucionou o conhecimento da natureza atômica da matéria e impulsionou o avanço dos fenômenos eletroeletrônicos. 13 REFERÊNCIAS [1] MACETI, H; LEVADA, C L; LAUTENSCHLEGUER, I J. Robert Millikan e a medida da carga elementar – 100 anos da publicação do trabalho que mudou a física. Caderno de física da UEFS. Feira de Santana-BA. V. 09. n. 01 e 02. p. 85-92. Jan-Dez. 2011. Disponível em: http://dfisweb.uefs.br/caderno/vol9n12/MacetiMillikan.pdf; Acessado em: 25/11/2019. [2] MELISSINOS, A.C., NAPOLITANO, J., Experiments in Modern Physics, Academic Press, an imprint of Elsevier Science, Second Edition.