Enviado por
common.user3806
motorccTeoria (1)

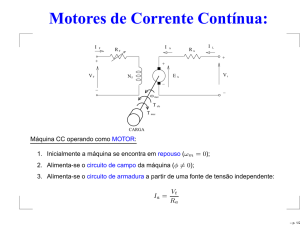
Motores de Corrente Contínua: I F I RF RA I L + + VF A + EA NF Vt − − − ω mec T ele T mec CARGA Máquina CC operando como MOTOR: 1. Inicialmente a máquina se encontra em repouso (ωm = 0); 2. Alimenta-se o circuito de campo da máquina (φ 6= 0); 3. Alimenta-se o circuito de armadura a partir de uma fonte de tensão independente: Ia = Vt Ra – p. 1/2 4. Cada condutor da armadura é percorrido por i = Iaa ⇒ Find = iBl ; 5. O torque induzido em cada condutor é calculado por: r τ = Find r sin θ Find l 6. O torque induzido nos condutores faz a armadura entrar em movimento (ωm > 0). τind = kt φIa onde kt = Find θ r Find cos θ Zp 2πa 7. A força contra-eletromotriz induzida na armadura (Ea = ke φωm ) limita a corrente da máquina: Ia = Vt − Ea Ra – p. 2/2 Tipos de motores CC: 1. Motor CC com excitação independente 2. Motor CC Shunt (em Derivação ) 3. Motor CC Série 4. Motor CC Composto Aditivo ou cumulativo (curto ou longo) Subtrativo ou diferencial (curto ou longo) 5. Motor CC de Ímãs permanentes 6. Motor CC sem escovas (Brushless DC Motor ) – p. 3/2 Motor CC com excitação independente: R aj F I ∆ V esc A − + RA RI RC I L + + RF + VF EA NF Vt − − FONTE I − Circuito de campo: V = R + R aj f If f F mm = Nf If Circuito de armadura: Ia = IL V = E + (R + R + R ) I + ∆V t a a c a esc i Ea = ke φωm τ ele = kt φIa – p. 4/2 Motor CC Shunt: I ∆ V esc A − + RA I RI L (RF + Raj ) EA − NF I Vt F FONTE + + − Circuito de campo: V = V = R + R t aj f f If F mm = Nf If Circuito de armadura: Ia = IL − If V = E + (R + R ) I + ∆V t a a esc i a Ea = ke φωm τ ele = kt φIa – p. 5/2 Característica terminal do Motor Shunt: Desprezando as perdas no motor CC tem-se que: ωm Ra (k φ) 2 VT kφ τele = τcarga + τperdas ≈ τcarga Desprezando as quedas de tensão nas escovas e no enrolamento de interpólo tem-se: τele = kt φIa Vt = Ea + Ra Ia (1) Ea = ke φωm τ → Ia = ele kt (2) τ ωm ele (3) Substituindo (3) e (2) em (1) tem-se: Vt Ra = − τ 2 ele kφ (kφ) τ carga ρω (%) = ωvazio − ωplena carga ωplena carga 100 onde ω é constante. – p. 6/2 A REAÇÃO DA ARMADURA enfraquece o fluxo polar; O enfraquecimento de φ diminui a amplitude da tensão induzida Ea forçando o aumento da corrente Ia , do torque τele e conseqüentemente da velocidade do motor ωm VT kφ Ra (k φ) 2 Com RA Sem RA τ carga τ ele – p. 7/2 Controle de velocidade de Motores Shunt Da observação de Vt Ra τele ωm = − 2 kφ (kφ) pode-se derivar três estratégias de controle para o motor CC. 1. Variação do fluxo magnético (φ) produzido no campo através do ajuste da resistência (Raj ); 2. Variação da tensão de alimentação da armadura (Va ); 3. Conexão de uma resistência adicional em série com o circuito da armadura (Rad ); – p. 8/2 Variação do fluxo magnético (φ): ωm ω m2 I I A L + RA ω m1 RF + Vt EA − R F2 > R F1 NF I F R F2 − R F1 τ carga τ ele – p. 9/2 Variação da tensão de armadura (Va): ωm I I A VA1 L VA2 RA + EA − CONVERSOR CC−CC + VA RF Vt NF I F − VA3 kφ Ra (k φ) 2 kφ kφ VA4 kφ τ carga τ ele – p. 10/2 Variação da resistência de armadura (Rad) ωm I A I R ad L + RA ωm RF R a < R a1< R a2 < R a3 + Vt EA − NF I F − Ra R a1 R a2 τ carga R a3 τ ele – p. 11/2 Motor CC série: RA I NS RS A I L + + I S Vt EA − − Circuito de campo: Circuito de armadura: Ia = IL = Is V = E + (R + R ) I t a a s a Ea = ke φs ωm τ ele = kt φIa φs ∝ Ia → φs = k1 Ia τele = kt φs Ia = kt (k1 Ia ) Ia τele = kt′ Ia2 – p. 12/2 Característica terminal do Motor Série: Como ke = kt = k no SI tem-se: τele = k′ Ia2 → Ia = r ωm τele k′ e, Ea = kφωm ω m1 Substituindo as expressões acima em Vt = Ea + (Ra + Rs ) Ia tem-se: τ Vt = kφωm + (Ra + Rs ) q τele k′ q = k (k1 Ia ) ωm + (Ra + Rs ) Reescrevendo a equação anterior explicitando ωm tem-se: ωm = Vt Ra + Rs − √ k′ τele k′ τ ele1 part τ ele τele k′ para ωm = 0, τpart = k′ Vt Ra +Rs 2 – p. 13/2 Partida de motores cc A corrente dos motores CC durante a partida é limitada apenas pela resistência da armadura Ra . I I A Ea = kφω = 0 L ⇓ + RA RF + Vt EA − NF I F − Vt − E a Ia = Ra ⇓ Na partida ω = 0, logo Vt Ia = Ra A corrente de partida dos motores CC pode chegar até a 30 x Ianominal – p. 14/2 A medida que o motor acelera a tensão Ea cresce forçando a corrente Ia diminuir. Exemplo: Motor CC independente Partida de motor CC 5HP/240V 400 Ia [A] ~ 328 A 16,2 A 200 0 −200 0 1 2 3 4 5 6 7 8 9 10 Torque [Nm] 600 400 29,25 Nm 200 f 0 −200 0 1 2 3 4 5 6 7 8 9 10 Para este motor ω [rpm] 1500 1000 X: 8.832 Y: 1221 Ia = 1221 rpm 500 0 5HP/240V I anominal = 16, 2A Ra = 0, 73Ω R = 240Ω 0 1 2 3 4 5 Tempo [s] 6 7 8 9 Vt 240V ≈ 330A = Ra 0, 73 10 – p. 15/2 Para limitar a corrente de partida podemos projetar um resistor Rp para ser inserido em série com a armadura. I Ap I Rp Como exemplo suponha que deseja-se uma corrente de partida ser menor que 210 % da nominal Lp Iap ≤ 210%Ianominal = 34A + RA RF + Vt EA − NF I Iap = F − Rp ≥ Vt ≤ 34A Ra + Rp 240V − 0, 73Ω = 6, 33Ω 34A Desvantagens: Perdas elevadas; Corrente e velocidade não atingem o valor nominal – p. 16/2 Ia [A] 40 20 0 −20 11,72 A 0 1 2 3 4 5 6 7 8 9 10 Torque [Nm] 100 21.21 Nm 50 0 −50 0 1 2 3 4 5 6 7 8 9 10 9 10 ω [rpm] 1000 500 862 rpm 0 0 1 2 3 4 5 Tempo [s] 6 7 8 – p. 17/2 Para resolver o problema anterior pode-se colocar uma chave em paralelo com o resistor Rp . Essa chave Sw é fechada depois de um tempo e fornece um caminho para a corrente da armadura. Sw I I Ap Lp + Rp RA RF + Vt EA − NF I F Contudo depois que a chave Sw é fechada como a velocidade e a tensão Ea não são nominais a corrente de armadura sofre um outro pico (que geralmente é elevado também) − – p. 18/2 Contudo o resistor Rp pode ser dividido em n estágios os quais são retirados a medida que o motor acelera. Partida de motor CC 5HP/240V com banco de resistores Ia [A] 40 S3 20 ° 2 estágio saída do 1° estágio 0 −20 0 2 4 6 S2 S1 3° estágio I 8 Torque [Nm] 100 + 50 R3 RA 0 −50 Ap 10 R2 R1 + 0 2 4 6 8 10 Vt ω [rpm] 1500 EA 1000 500 0 − 0 2 4 6 8 10 − Tempo [s] – p. 19/2 Metodologia de cálculo dos resistores: 1. Projeta-se o resistor Rp para que a corrente de partida ou o torque não sejam superior a um valor máximo especificado pelo projeto Iap ≤ Iamáx ou, τp ≤ τmáx 2. O resistor Rp é então divido em n-estágios Rp = R1 + R2 + R3 + . . . + Rp 3. Considerando que a resistência Rp = R1 + R2 + R3 + . . . + Rn está totalmente inserida no circuito de armadura tem-se que a corrente de partida é menor que Iamáx e pode-se escrever a seguinte equação: Vt = Ea + Ra Iamáx + (R1 + R2 + R3 + . . . + Rn ) Iamáx + ∆Vesc = Ea + (R1 + R2 + R3 + . . . + Rn + Ra ) Iamáx + ∆Vesc Vt = Ea + Rtot Iamáx + ∆Vesc (4) – p. 20/2 4. A medida que o motor acelera ω a tensão Ea cresce e a corrente Ia diminui. Quando o valor da corrente da armadura chega a um limite mínimo Iamín pode-se reescrever (4) como: Vt = Ea + Rtot Iamín (5) 5. Neste instante fecha-se a chave S1 . O resistor R1 é retirado do circuito e a corrente do motor volta a crescer. Contudo a mesma deve ser menor que Iamín . Desse modo, considerando Rtot,1 = R2 + R3 + . . . + Rn + Ra , tem-se: Vt = Ea + Rtot,1 Iamáx (6) Ea + Rtot Iamín = Ea + Rtot,1 Iamáx (7) 6. Igualando (5) e (6) tem-se: Rtot,1 = Iamín Iamáx Rtot (8) – p. 21/2 6. Aplicando essa metodologia sucessivamente tem-se que a resistência depois de retirado o n-ésimo estágio é dada por: Rtot,n = Ra = Iamín Iamáx n Rtot (9) Ou seja, n= Ra Rtot Ia mín Iamáx 7. As resistências de cada estágio podem ser facilmente calculadas resolvendo o sistema: R1 + R2 + R3 + . . . + Rn + Ra = Rtot R2 + R3 + . . . + Rn + Ra = Rtot,1 R3 + . . . + Rn + Ra = Rtot,2 .............................. Ra = Rtot,n = (Rp + Ra ) (10) – p. 22/2 Rendimento e perdas nos motores cc: 1. Perdas no COBRE: (a) na armadura ⇒ Ra Ia2 2 (b) no campo ⇒ Raj + Rf If 2. Perdas no FERRO: (a) por histerese; (b) por correntes parasitas (corrente de Foucault) 3. Perdas no MECÂNICAS (atrito e ventilação): 4. Perdas nas ESCOVAS ⇒ ∆Vesc Ia 5. Perdas SUPLEMENTARES ⇒ 1% da potência nominal do motor. – p. 23/2 Potência elétrica (de entrada): Pele = Vt IL I A I RA Potência elétrica entregue ao rotor: L Pint = Ea Ia + + τ ele τ mec ω RF Vt EA − NF I Potência mecânica (de saída): F Pmec = τmec ω = τele ω − Pmec = Ea Ia − Perdas no rotor Rendimento: η= Pmec τ ω ×100% = mec ×100% Pele Vt IL – p. 24/2 Ensaios 1. Ensaio a vazio: ⇒ usado para determinar as perdas rotacionais do motor Perdas rotacionais = Eavaz Iavaz 2. Ensaio de rotor bloqueado: ⇒ usado para determinar a resistência da armadura Vt − ∆Vesc Ra = Ianom – p. 25/2