ri-2014-art9-barbosa

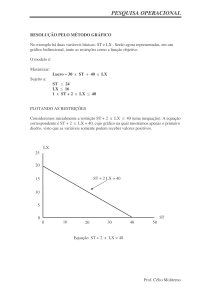
2014 • ANO XX, Nº 66 • 49-58
INTEGRAÇÃO
49
Utilização da programação linear na otimização
de resultados de produção na empresa
GERALDO MAGELA BARBOSA*
Resumo • A formulação de problemas no ambiente empresarial consiste na descrição de um sistema estruturado
com o auxílio de um modelo. Após a experimentação com o modelo e analisando seus objetivos e limitações se
determinará a melhor forma de operar o sistema. A técnica de programação linear abordada neste artigo irá indicar
qual a combinação na produção que trará o melhor resultado possível, e em outra aplicação suprir os pedidos de
forma a minimizar os custos de produção de uma indústria.
Palavras Chave: Programação linear, otimização de resultados, produção.
Abstract • The formulation of problems in the business environment constitutes a structured description with the
aid of a model system. After experimenting with the model in a company and analyzing your goals and limitations
determine how best to operate the system. The linear programming technique in this article which will resolve the
production of two products that a company has the highest possible profit, and meet other application requests to
minimize production costs of an industry.
Keywords: Linear programming, optimization results, production.
1. Introdução
A programação linear é uma das técnicas mais utilizadas na solução de problemas. É um método científico
de tomada de decisões. Estas técnicas foram desenvolvidas inicialmente para necessidades militares em alocar
recursos escassos às várias operações militares e às atividades dentro de cada operação de uma maneira efetiva.
Segundo uma pesquisa realizada em Londres a programação linear é uma das ferramentas mais utilizada
para tomada de decisões além do modelo de regressão.
Durante a segunda guerra mundial, a United States Air Force organizou um grupo de pesquisadores
de nome SCOOP (Scientific Computation of Optimum
Program), sob a direção de Marshall K. Wood para solucionar o problema de alocação de recursos limitados
de modo a otimizar objetivos (LOESCH; HEIN,2009).
A otimização de problemas com funções lineares,
denominadas funções objetivos, levando em conta as
equações restritivas (também lineares) consiste a ferramenta matemática mais utilizada na tomada de decisões que é a programação linear.
O problema de otimizar uma função linear sujeita a restrições teve a sua origem com os estudos
de Fourier sobre sistemas lineares de inequações em
1826. No entanto só em 1939 Kantorovich faz notar
a importância prática destes problemas, tendo criado
um algoritmo para a sua solução.
O auge do estudo de problemas de otimização de
uma função linear sujeita a restrições foi com George
*É mestre em Engenharia pela Escola Politécnica da Universidade
de São Paulo - USP, Engenheiro Mecânico com ênfase em Produção pela Universidade Federal de Itajubá - UNIFEI. É licenciado em
Matemática pelo Centro Universitário de Itajubá - UNIVERSITAS e
professor da Universidade São Judas Tadeu - USJT.
e-mail: [email protected]
Dantzig na década de 1940, nos Estados Unidos. Dantzig não só formulou o problema de programação linear,
mas também criou o algoritmo do Simplex em 1947.
A aplicação da programação linear em uma empresa permite resolver problemas como, a otimização da distribuição, a programação da produção e a
alocação de recursos. A programação linear tem sido
utilizada na busca de soluções para os problemas de
otimização nas mais diferentes atividades, como em
indústrias, bancos e empresas de transporte e que tem
gerado maiores lucros.
Uma pesquisa em 51 cursos de administração nos
Estados Unidos revelou que o principal objetivo dos cursos que envolvem Programação Linear, enunciado por
87,5% dos respondentes, era o de “melhorar a habilidade
quantitativa gerais dos estudantes”. Em seguida foram citados os objetivo de “ensinar técnicas quantitativas que
os alunos possam usar quando gerentes”. Nota-se que a
Programação Linear, trás um melhor raciocínio lógico,
melhora a capacidade de estruturar e resolver problemas
e ainda conhecer técnicas úteis que será aplicada na vida
profissional de um executivo (MOREIRA, 2010).
O desenvolvimento da programação linear tem
sido classificado entre os mais importantes avanços
científicos dos meados do século XX. Seu impacto
desde 1950 tem sido extraordinário. Hoje é uma ferramenta padrão que poupou milhares de dólares para
muitas empresas ou até mesmo negócios de porte médio em diversos países industrializados ao redor do
mundo (HILLIER; LIEBERMAN, 2013).
Os gerentes das organizações, constantemente se deparam com circunstâncias em que devem tomar decisões,
que levam em consideração diversas alternativas conflitantes e concorrentes, diante dessas situações os gerentes podem utilizar a intuição gerencial ou realizar um processo
de modelagem da situação (LACHTERMACHER, 2007).
50
INTEGRAÇÃO
A programação linear, especificamente, oferece
aos gerentes a capacidade de tomar decisões mais eficazes e de estabelecer sistemas mais produtivos, por
meio de informações mais completas realizam-se previsões cuidadosas de resultados e estimativas de risco
com ferramentas atuais e técnicas de decisão.
Em linhas gerais, a programação linear busca, entre as inúmeras tarefas ou atividades, descobrir a melhor
distribuição dos recursos a fim de obter um valor ótimo
do objetivo desejado. Os problemas de alocação de recursos distinguem-se pela existência de um objetivo explícito por meio de variáveis de decisão e pela existência de
restrições para alocar os recursos devido às quantidades
disponíveis e a forma de aplicá-los (ANDRADE, 2007).
2. Maximização do lucro da empresa e
as restrições na produção
O modelo matemático de programação linear é
composto de uma função objetivo linear, e de restrições técnicas representadas por um grupo de inequações também lineares (SILVA, 2010).
No desenvolvimento de um modelo de programação linear, algumas características devem ser levadas em
consideração, tais como indicadas por PASSOS (2008):
• Os modelos apresentarão restrições (equações e/ou
inequações) lineares, bem como a sua função objetivo,
• Os valores variarão a uma taxa constante dos
recursos utilizados (linearidade das restrições e
da função objetivo),
• As variáveis podem assumir valores em um intervalo (contínuas),
• Os valores assumidos pelas variáveis serão nulos ou positivos (não negatividade).
Os bons modelos serão os mais próximos da realidade e de fácil experimentação. Nos modelos matemáticos as relações entre as variáveis do problema
devem ser representadas por sistemas de símbolos e
relações matemáticas. Os principais elementos que
BARBOSA • Utilização da programação linear
existem em um modelo matemático são:
• Variáveis de decisão e parâmetros: por meio da
função-objetivo, surgem variáveis fundamentais,
essas variáveis são denominadas de variáveis de decisão. Os parâmetros são valores fixos no problema;
• Restrições: retratam a insuficiência dos recursos
e os limites impostos sobre as ações, com o objetivo de maximizar a função-objetivo;
• Função Objetivo: é uma função matemática formada
por uma combinação linear das variáveis de decisão.
Conseguir uma solução ótima, ou seja, a melhor
de todas, é a ideia fundamental na solução de um
problema, mas isso exige a solução de um sistema de
equações e inequações como na programação linear.
Considere o problema de Maximização de Lucro
de uma empresa que está logo em seguida. O problema
será estruturado e solucionado utilizando o Modelo
Matemático de Programação Linear.
Uma empresa vende dois tipos de produtos, P1 e
P2, cujos lucros unitários são de R$ 80,00 e R$ 60,00
respectivamente.
Sabe-se que os dois produtos P1 e P2 são produzidos em três processos sequenciais que são: retificação,
perfuração e polimento.
O processo de retificação dispõe de máquinas que
fornecem um total de 160 horas de retificação por semana. Cada produto precisa de 2 horas de retificação.
O processo de perfuração dispõe de máquinas
que fornecem um total de 120 horas por semana. O
produto P1 exige 1 hora de perfuração e o produto P2
exige 2 horas de perfuração.
O processo de polimento é intensivo com relação
á mão-de-obra fornecendo 280 horas de mão-de-obra
por semana. O produto P1 requer 4 horas de mão-de-obra por unidade, o produto P2 requer 2 horas de
mão-de-obra por unidade.
O Departamento de Marketing informou que
consegue vender, semanalmente, no máximo 75 unidades do produto P1 e 70 unidades do produto P2.
As tabelas a seguir representam as informações:
Tabela 1. Lucros unitários na venda dos produtos
Tabela 2. Fatores necessários para a produção dos Produtos P1 e P2
2014 • ANO XX, Nº 66 • 49-58
51
INTEGRAÇÃO
Com base nestes dados, pergunta-se: qual a produção mensal dos Produtos P1 e P2 para que a empresa tenha o maior lucro possível?
Como se quer maximizar o lucro será utilizada uma
função na qual fará parte os lucros apurados nas vendas
de cada modelo vezes a quantidade que deverão ser produzidas. Sendo assim, a função objetivo será composta
pela soma do produto do lucro unitário de cada modelo
vezes as suas respectivas variáveis de decisão.
limitadas a 280 horas por semana
E ainda que a inequação acima identifica a disponibilidade limitada do processo de polimento
A demanda semanal de vendas pelo Departamento de Marketing é
2.1 Estruturando o problema: construção do modelo matemático
O método científico de programação linear começa com a definição do problema a mais precisa
possível, na qual devem ser destacados os objetivos
procurados, as características de interligação entre as
diferentes variáveis existentes e as restrições do sistema (ELLENRIEDER, 1971).
O objetivo desta empresa é de maximizar o lucro
na produção semanal dos produtos P1 e P2, com base
nos dados do problema que estão na Tabela. 1 e Tabela
2.monta-se a Modelagem Matemática a seguir:
As Variáveis de Decisão x1 e x2 são dadas por:
{
x1 = representa a quantidade a produzir do produto P1
x2 = representa a quantidade a produzir do produto P2
A função objetivo é a Maximização do Lucro
(Lmáx) que é dado por:
Lmáx = 80 x1 + 60 x2
Os processos sequenciais de retificação, perfuração e polimento e as suas respectivas disponibilidades
para fabricação dos produtos P1 e P2, conforme a Tabela 2. permite escrever:
a) do processo de retificação serão utilizados 2
horas para o produto P1 e 2 horas para o produto P2
limitadas a 160 horas por semana
2 x1 + 2 x2 ≤ 160
Esta inequação reflete a disponibilidade limitada
do processo de retificação
b) do processo de perfuração serão utilizados 1
hora para o produto P1 e 2 horas para o produto P2
limitadas a 120 horas por semana
1 x1 + 2 x2 ≤ 120
Sendo que esta inequação mostra a disponibilidade limitada do processo de perfuração
c) do processo de polimento serão utilizados 4
horas para o produto P1 e 2 horas para o produto P2
4 x1 + 2 x2 ≤ 280
x1 ≤ 75
x2 ≤ 70
Sendo que as variáveis de decisão não podem ser
negativas pois representam os produtos na modelagem, temos:
x1 ≥ 0
x2 ≥ 0
2.2 A solução gráfica para a maximização
O objetivo principal é determinar o maior lucro
semanal possível para a empresa, considerando as restrições dos fatores de produção. Sabendo que para a produção do produto P1 e do produto P2 requerem os processos sequenciais de retificação, perfuração e polimento.
Com a estrutura de Modelagem Matemática anterior, o problema de programação linear está completo, como especificado abaixo:
As Variáveis de Decisão x1 e x2 são dadas por:
{
x1 = representa a quantidade a produzir de P1
x2 = representa a quantidade a produzir de P2
Maximização do Lucro: Lmáx = 80 x1 + 60 x2
Que dependem das Restrições Técnicas:
{
2 x1 + 2 x2 ≤ 160 (restrição na retificação)
1 x1 + 2 x2 ≤ 120 (restrição na perfuração)
4 x1 + 2 x2 ≤ 280 (restrição no polimento)
A demanda semanal de vendas pelo Departamento de Marketing é
{
x1 ≤ 75
x2 ≤ 70
As Restrições de Não Negatividade das variáveis
de decisão são:
{
x1 ≥ 0
x2 ≥ 0
Determinam-se os valores das quantidades x1 e
x2 sem violar as restrições. Assim, colocando as Restri-
52
INTEGRAÇÃO
ções de Retificação, Perfuração e Polimento em um mesmo sistema de eixos cartesianos obtém-se o Gráfico 1.
O problema da programação linear para a fabricação é determinar uma combinação de x1 e x2 que
permita maximizar o lucro, dadas as restrições de fatores de produção. No gráfico acima, podemos notar que
o maior lucro que intercepta a região viável (fronteira
de possibilidades) de produção são os pontos C e D.
No Gráfico 1 observa-se que, se considerarmos
apenas uma das restrições, a empresa poderá produzir
qualquer uma das alternativas entre x1 e x2 e continuar
a satisfazer a restrição. Por exemplo, a empresa pode
produzir, nos extremos, 140 quantidades semanais de
x2 e nada de x1, sem se afetar pela restrição do fator de
produção da perfuração, bem como 120 quantidades
semanais de x1 e nada de x2 sem se afetar pela restrição
do fator de produção do polimento.
A empresa tem de levar em consideração todas
as restrições existentes para seus fatores de produção e,
consequentemente, estará habilitada a produzir apenas
as combinações entre e que estiverem dentro da região
viável determinada pelas três retas de restrição (retificação, perfuração e polimento), bem como sobre a linha da
região viável (fronteira de possibilidades) de produção.
BARBOSA • Utilização da programação linear
A função objetivo de maximização do lucro
para a empresa na estrutura do problema é dado por
Lmáx = 80 x1 + 60 x2
Nesta função que gera o lucro máximo para a empresa especifica que a margem de contribuição total da
empresa é igual a R$ 80,00 vezes a quantidade de x1
mais R$ 60,00 vezes a quantidade de x2 produzida.
Para a identificação do ponto ótimo (que torna o lucro máximo), deve-se avaliar o desempenho da função
objetivo atribuindo valores a Lmáx. Ao se arbitrar valores para Lmáx, se obtém equações onde as retas traçadas
são paralelas e que se deslocam no mesmo sentido.
Ao se arbitrar R$ 6.000,00 em Lmáx encontra-se a
equação 6000 = 80 x1 + 60 x2 que fornece o conjunto de
pontos de (x1 , x2) que resultarão em 6000. Os pontos
(0,100) e (75,0) dão uma margem de contribuição de
R$ 6000,00 conforme a reta traçada no Gráfico 2.
Arbitrando o valor de R$ 7.000,00 em Lmáx encontra-se a equação 7000 = 80 x1 + 60 x2 que fornece o
conjunto de pontos de (x1 , x2) que resultarão em 7000.
Os pontos (0;116,67) e (87,5;0) dão uma margem de
contribuição de R$ 7000,00 conforme reta traçada no
Gráfico 2 que será paralela a reta anterior.
Se a empresa deseja maximizar o lucro, então ela
deverá estar na mais distante reta possível com as restrições dos fatores de produção.
Pode-se notar no Gráfico 2 que a reta para Lmáx
= R$ 6000,00 intercepta o ponto D (60,20) da região
viável de produção.
O Lucro Máximo é de R$ 6000,00 que é o maior
montante que a empresa pode encontrar, dada a sua
capacidade de produção.
Gráfico 1. Retas de Restrição (Retificação, Perfuração e Polimento)
e a Região Viável.
A combinação na produção de x1 e x2 nesta área
sombreada determinará a região viável de produção.
Com o gráfico gerado pelas restrições, a empresa poderá produzir qualquer combinação de x1 e x2 que estiver na região viável de produção. O objetivo da empresa é que se deseja produzir a combinação de x1 e x2
que lhe permita maximizar seu lucro. Para atingir esta
meta, a empresa deverá conhecer a margem de contribuição por unidade produzida e vendida para cada
produto que ela produz.
Desta forma tem-se, neste problema, que a margem de contribuição de x1 é de R$ 80,00 por unidade e
de x2 é de R$ 60,00 por unidade.
Gráfico 2. Retas Paralelas a Região Viável de Maximização do Lucro.
O ponto D (60,20) indica a contribuição que maximiza o lucro na produção combinada de x1 e x2 que a
empresa pode produzir nestas condições.
Substituindo x1= 60 e x2= 20 na função de Lucro
Máximo
Lmáx = 80 x1 + 60 x2 se obtém:
2014 • ANO XX, Nº 66 • 49-58
Lmáx = 80(60) + 60(20) = 4800 + 1200
Que resulta Lmáx = R$6.000,00, que é o Maior
Lucro possível.
Portanto, o ponto D(60,20) é o Ponto Ótimo,
mesmo que a empresa tenha capacidade ociosa de algum fator de produção, logo o Lucro Máximo é de R$
6000,00.
2.3. Solução algébrica para a maximização
Os métodos algébricos são bem mais precisos e
práticos, especialmente quando nos defrontamos com
um número de variáveis maior que dois especialmente
porque graficamente a análise se torna mais difícil.
Há vários métodos algébricos para a solução de
problemas, como o que está sendo verificado neste artigo, e essas soluções são ainda disponíveis por meio
dos mais diferentes softwares sobre o assunto.
Neste trabalho, será apresentado apenas o método algébrico mais simples.
Na estruturação do problema tem-se que
As Variáveis de Decisão x1 e x2 são dadas por:
{
x1 = representa a quantidade a produzir do produto P1
x2 = representa a quantidade a produzir do produto P2
A função objetivo da empresa que é Maximizar o
seu Lucro é :
Lmáx = 80 x1 + 60 x2
As Restrições nos processos de fabricação dos
produtos são
{
2 x1 + 2 x2 ≤ 160 (restrição na retificação)
1 x1 + 2 x2 ≤ 120 (restrição na perfuração)
4 x1 + 2 x2 ≤ 280 (restrição no polimento)
A demanda semanal de vendas é
{
x1 ≤ 75
x2 ≤ 70
As Restrições de Não Negatividade são:
{
53
INTEGRAÇÃO
x1 ≥ 0
x2 ≥ 0
Para se resolver o problema algebricamente, sabe-se que os pontos que determinam o limite (também denominados pontos extremos) da região viável (fronteira
de possibilidades) de produção ocorrem:
a) onde duas retas de restrição se encontram (interceptam);
b) onde a reta de restrição intercepta tanto o eixo
das abscissas como o eixo das ordenadas;
c) no ponto de origem.
O ponto de origem A é quando se tem x1 = 0 e
x2= 0, logo A (0,0).
A equação da reta de Restrição da Retificação
associada a inequação estruturada na formulação do
problema é dada por: 2x1 + 2x2 = 160. Para encontrar
os pontos extremos F e H, substitui-se respectivamente na equação x1 = 0 e x2 = 0, onde se obtém: F(0,80) e
H(80,0), conforme Gráfico 1.
Na equação da reta de Restrição da Perfuração
associada a inequação estruturada na formulação do
problema que é: 1x1 + 2x2 = 120. Para encontrar os
pontos extremos B e I, substitui-se respectivamente
na equação x1 = 0 e x2 = 0 onde se obtém: B(0,60) e
I(120,0).
E ainda temos que, na equação da reta de Restrição de Polimento associada a inequação estruturada
na formulação do problema que é dada por :
4x1 + 2x2 = 280. Para encontrar os pontos extremos G
e E, substitui-se respectivamente na equação x1 = 0 e x2
= 0 , onde se obtém: G(0,140) e E (70,0), que pose ser
visto no Gráfico 1.
O ponto de intersecção C das retas de equações
de Restrição da Retificação e da Perfuração é:
2x1 + 2x2 = 160
1x1 + 2x2 = 120
Multiplicando por –1 a segunda equação temos:
2x1 + 2x2 = 160
-1x1 - 2x2 = 120
_____________
x1= 40
Substituindo-se x1= 40 em qualquer uma das
equações de Restrição encontra-se x2= 40. O ponto de
intersecção C das retas é dado por C(40,40).
O ponto de intersecção D das retas de equações
da Restrição do Polimento e Retificação é:
4x1 + 2x2 = 280
2x1 + 2x2 = 160
Multiplicando por –1 a segunda equação temos:
4x1 + 2x2 = 280
-2x1 - 2x2 = -160
_____________
2x1= 120
x1= 60
Logo se obtém x1= 60. Substituindo-se x1= 60 em
qualquer uma das equações de restrição, encontra-se
x2= 20. O ponto de intersecção D das retas é dado por
D(60,20).
54
INTEGRAÇÃO
BARBOSA • Utilização da programação linear
Temos todos os pontos extremos das retas, os
pontos de origem e os pontos onde as retas interceptam os eixos da abscissa e ordenada.
Sabendo que a demanda semanal de vendas pelo
Departamento de Marketing é x1 ≤ 75 e x2≤ 70 . Conclui-se que os pontos F(0,80) com coordenada x2= 80,
G(0,140) com coordenada x2 = 140, H(80,0) com coordenada x1 = 80 e I(120,0) com coordenada x1 = 120
não serão utilizados, pois estão fora da Restrição de
Demanda, conforme pode ser visto no Gráfico 2.
Como o objetivo da empresa é determinar o
maior lucro possível, substitui cada par ordenado dos
pontos na função de lucro máximo obtida na formulação do problema.
Todos os pares ordenados dos pontos A, B, C,
D, E serão substituídos na função de Lucro Máximo
Lmáx = 80 x1 + 60 x2 . Os valores obtidos são todas as
soluções da função objetivo que estão na Tabela 3.
Tabela 3. Soluções da função objetivo para a maximização
Com os valores obtidos da função objetivo, verificasse
que o lucro máximo semanal é obtido no ponto D(60,20)
onde x1= 60 e x2= 20 gerando Lmáx= R$ 6000,00.
Este resultado é a Solução Ótima da empresa, ou
seja, o Lucro Máximo é de R$ 6000,00.
Onde se deve produzir 60 unidades do produto
P1 e 20 unidades do produto P2 para que se tenha um
lucro máximo de R$ 6000,00 semanalmente.
Conforme se determinou graficamente, a combinação ótima na produção dos produtos e , algebricamente,
é dada também pelo ponto D, onde x1= 60 , x2= 20 e
Lmáx= R$ 6000,00, o mais alto nível de Maximização
do Lucro obtido neste trabalho.
Observa-se que sempre é bom utilizar a análise gráfica juntamente com o método algébrico para
se encontrar o ponto de maximização do lucro para
que se possa localizar, mais facilmente, os pontos da
fronteira da região viável (possibilidades) de produção
(enquanto o número de variáveis de decisão não for
muito extenso).
O procedimento algébrico para incluir as variáveis de folga se baseia na transformação das inequações (restrições) em equações igualmente equivalentes. Essa conversão é realizada incluindo-se variáveis
de folga (HILLIER; LIBERMAN, 2013).
As variáveis de folga (onde se utiliza S como variável de folga, pois vem do inglês Slack (folga)) para
cada recurso de produção será S1 (retificação) e S2
(perfuração) e S3 (polimento) transforma as equações
em:
{
2 x1 + 2 x2 + S1 = 160 (S1 é a variável de folga na retificação)
1 x1 + 2 x2 + S2 = 120 (S1 é a variável de folga na perfuração)
4 x1 + 2 x2 + S3 = 280 (S1 é a variável de folga no polimento)
A inclusão dessas variáveis de folga transforma
essas restrições em igualdades algébricas, porque o
montante de um particular tipo de fator de produção
utilizado na produção, mais a capacidade ociosa que
sobra dela, tem de ser igual à quantidade total disponível desse fator.
Para o processo de fabricação dos produtos na
Retificação que se tem a equação dada para o cálculo
da variável de folga 2 x1 + 2 x2 + S1 = 160 calcula-se a
variável de folga S1 substituindo o Ponto Ótimo D (
60,20 ), ou seja, x1 = 60 , x2 = 20 que fica:
2(60) + 2(20) + S1 = 20
120 + 40 + S1 = 20
S1 = 0
2014 • ANO XX, Nº 66 • 49-58
INTEGRAÇÃO
Logo, o valor da variável de folga é S1 = 0, este
resultado significa que o recurso de operação de Retificação está em pleno emprego pois determina a capacidade de produção (gargalo) da empresa.
Na fabricação dos produtos na Perfuração que se
tem a equação dada para o cálculo da variável de folga
1 x1 + 2 x2 + S2 = 120 calcula-se a variável de folga S2
substituindo o Ponto Ótimo D ( 60,20 ), ou seja,
x1 = 60, x2 = 20 que fica:
1(60) + 2(20) + S2 = 120
60 + 40 + S2 = 120
S2 = 20
55
Através da programação linear será apresentado a
solução para o problema de minimização. As abordagens a serem utilizadas são análogas à que foi utilizada
no problema de maximização.
Um problema de programação linear (programação matemática) com o objetivo de minimizar
uma quantidade específica depende de um número
finito de variáveis de entrada. Estas variáveis podem ser independentes uma das outras ou podem
ser relacionadas por meio de uma ou mais restrições
(BRONSON, 1985).
3.1 Estruturando o problema
Resultando no valor da variável de folga S2 =20,
isto significa que se tem 20 horas-máquinas de ociosidade por semana na Perfuração.
E que fabricação dos produtos no Polimento que
se tem a equação dada para o cálculo da variável de
folga 4 x1 + 2 x2 + S3 = 280 a variável de folga S3 é obtida
substituindo o Ponto Ótimo D ( 60,20 ), ou seja, ,
x1 = 60, x2 = 20que fica:
4(60) + 2(20) + S3 = 280
240 + 40 + S3 = 280
S3 = 0
Onde se tem que a o valor da variável de folga
é S3 = 0, este resultado significa que o recurso de operação de Polimento está em pleno emprego pois determina a capacidade de produção (gargalo) da empresa.
3. Minimização de custos com o uso da
Programação linear
A técnica da programação linear resolve problemas com o objetivo de minimizar as despesas na
fabricação de produtos, minimizar o custo total de
produção e ainda identificar e modelar problemas
de tomada de decisão sobre a alocação de recursos
(ANDRADE, 2011).
Para problemas de decisão de minimização
de custos, também faz-se uso da programação linear. Anteriormente, se mostrou como se obtém
a combinação ótima na produção entre dois produtos, de acordo com as restrições existentes nos
fatores de produção, com o objetivo de se obter o
maior lucro possível.
Na programação linear, o modelo é uma representação matemática aproximada da realidade. O modelo deve ser formulado para captar o ponto crucial do
problema, por exemplo, minimização, para em seguida ter uma tomada de decisão e atingir um equilíbrio
apropriado entre a realidade e a aplicação da solução
(WAGNER, 1986).
Considere o problema de Minimização de Custo
de uma indústria que está logo em seguida. O problema será estruturado e solucionado utilizando o Modelo Matemático de Programação Linear.
Duas fábricas F1 e F2 produzem 3 diferentes tipos
de papel.
A companhia que controla as fábricas tem um contrato para produzir 60 toneladas de Papel Fino, 90 toneladas de Papel Médio e 120 toneladas de Papel Grosso.
O custo de produção na fábrica F1 é de R$ 1.000,00
por dia e o da fábrica F2 é de R$ 2.000,00 por dia.
A fábrica F1 produz 1 toneladas de papel fino , 2 toneladas de Papel médio e 4 toneladas de papel grosso por dia.
A fábrica F2 produz 4 toneladas de papel fino , 2 toneladas de papel médio e 2 toneladas de papel grosso por dia.
O objetivo do empresário é obter quantos dias
cada fábrica deverá operar para suprir os pedidos de
forma a Minimizar os Custos na produção de papel.
As informações do problema são representas por
meio de tabelas a seguir:
Tabela 4. Custos de produção por dia em cada fábrica.
Tabela 5. Fatores necessários para a produção dos Papéis (Fino Médio e Grosso).
56
INTEGRAÇÃO
BARBOSA • Utilização da programação linear
O objetivo do empresário é obter quantos dias
cada fábrica deverá operar para suprir os pedidos de
forma a Minimizar os Custos de produção de papel.
A quantidade a ser minimizada é descrita como
uma função matemática dos recursos (variáveis de
decisão) escassos. As relações entre as variáveis são
formalizadas através de restrições ao problema expressas como equações e/ou inequações matemáticas (LACHTERMACHER, 2002).
Para Minimizar os Custos na produção de papel
nesta fábrica e suprir os pedidos, com base nos dados
do problema que estão na Tabela 4. e Tabela 5. monta-se a Modelagem Matemática a seguir:
As Variáveis de Decisão x1 e x2 são dadas por:
{
x1 = representa a quantidade de dias que deve operar a fábrica F1
x2 = representa a quantidade de dias que deve operar a fábrica F2
A função objetivo é a Minimização dos Custos
(Cmín) que é dado por:
Cmín= 1.000 x1 + 2.000 x2
Que dependem das restrições técnicas:
{
1x1 + 4x2 ≥ 60 (Restrição na fábrica de Papel Fino)
2x1 + 2x2 ≥ 90 (Restrição na fábrica de Papel Médio)
4x1 + 2x2 ≥ 120 (Restrição na fábrica de Papel Grosso)
E que as restrições de Não Negatividade das variáveis de decisão são:
{
x1 ≥ 0
x2 ≥ 0
3.2 A solução gráfica para a minimização
O modelo de programação linear descreve um
problema de forma concisa e que torna mais compreensível a estrutura geral do problema e ajuda
a revelar importantes relacionamentos de causa-efeito e que facilita o tratamento do problema
como um todo considerando todos os seus inter-relacionamentos de forma simultânea (HILLER;
LIEBERMAN, 2013).
O objetivo principal objetivo do empresário é obter quantos dias cada fábrica deverá operar para suprir
os pedidos de forma a minimizar os custos de produção de papel.
As Restrições do Papel Fino, Papel Médio e Papel
Grosso, são colocados em um mesmo sistema de coordenadas cartesianas, da mesma forma como feita no
problema anterior conforme está no Gráfico 3.
Observe que a região viável, agora, está acima e à direita das linhas de restrição, contrastando
com o que foi mostrado anteriormente, quando a
região viável estava abaixo e à esquerda das linhas
de restrição.
Gráfico 3. Retas de Restrição e a Região Viável de Minimização do Custo.
Isto acontece em função da natureza das restrições dos recursos. Na seção anterior, a restrição de
fatores tinha o formato de menor ou igual a, que restringiam as combinações das variáveis de decisão a um
ponto sobre ou dentro da região viável, quando mostrados graficamente.
No presente problema, os recursos escassos têm o
formato de maior ou igual a, que restringe as possíveis
combinações das variáveis de decisão a um ponto sobre ou acima das retas de restrição.
Para encontrar o conjunto de pontos de (x1 , x2)
que atendam os requisitos necessários ao Menor Custo, devemos pensar em termos de deslocamentos paralelos da equação de custo Cmín= 1.000 x1 + 2.000 x2 , a
partir do ponto de origem 0, em direção à nordeste, até
que a função custo encoste em algum ponto na fronteira de mínimo custo.
Substituindo R$ 5.000,00 em Cmín encontra-se a
equação 5000 = 1000 x1 + 2000 x2 que fornece o conjunto de pontos de (x1 , x2) que resultarão em 5000. Os
pontos (0,25) e (50,0) dão uma margem de contribuição
de R$ 5000,00 conforme a reta traçada no Gráfico 4.
Gráfico 4. Reta que Intercepta o Ponto de Mínimo Custo na Região Viável.
2014 • ANO XX, Nº 66 • 49-58
57
INTEGRAÇÃO
Nota-se no Gráfico 4 que a reta para Cmín=5000
toca primeiro na fronteira no ponto B(40,5) , que corresponde a 40 dias de operação na fábrica F1 e 5 dias
de operação na fábrica F2, sendo esta a Solução Ótima,
pois representa o Menor Custo entre todas as combinações.
Substituindo x1 =40 e x2=5 na função de custo mínimo
Cmín= 1.000 x1 + 2.000 x2 se obtém:
Cmín= 1.000(40) + 2.000(5)=40.000 + 10.000
Que resulta Cmín= R$ 50.000,00, que é o menor
custo possível.
Neste problema não há outra combinação que
possa satisfazer as restrições e gerar custos menores
que R$ 50.000,00.
3.3. Solução algébrica
A resolução do problema pela solução algébrica
é fundamental, da mesma forma quando a utilizamos
para obter o ponto para maximização do lucro.
Primeiramente, temos que encontrar os valores
de x1 e x2 para cada ponto da reta que representa o
menor custo possível, isto é, os pontos A, B, C e D determinados pela intersecção das retas de restrição que
passam por cada ponto.
Considerando o ponto B no Gráfico 4. que representa a intersecção das retas de restrição de Papel Fino
e Papel Médio.
Associando as inequações de restrição equações
temos:
1x1 + 4x2 = 60
2x1 + 2x2 = 90
Multiplicado a segunda equação por –2 temos:
1x1 + 4x2 = 60
-4x1 + -4x2 = -180
______________
-3x1 = -120
x1 = 40
Encontra-se o valor =40 que substituído este valor na primeira equação, tem-se:
1(40) + 4x2 = 60
40 + 4x2 = 60
x2 = 5
Obtém-se x 2 = 5, assim, o ponto B é dado por
x1 = 40 e x2 = 5, ou seja, B (40,5).
Repetindo este procedimento para os demais
pontos A, C e D se obtêm as combinações de dias de
operação das fábricas.
Com as combinações dos pares de pontos A, B,
C e D calculam-se os respectivos Custos Mínimos que
constam na Tabela 6.
Tabela 6. Soluções da função objetivo para a minimização
Ao observar a tabela acima, o Ponto Ótimo em
que o se deve Operar as Fábricas e Minimizar o Custo
é o ponto B de coordenadas x1 = 40 e x2 = 5.
Não existe outra combinação possível que
possa satisfazer as restrições a um menor custo de
R$ 50.000,0 conforme os valores da Tabela 6 para
custo mínimo.
Com este resultado, deve-se operar a Fábrica F1
em 40 dias e a Fábrica F2 em 5 dias para atender a solicitação de contrato, suprindo os pedidos de forma a
Minimizar os Custos na Produção de Papel.
58
INTEGRAÇÃO
4. Considerações finais
O método da programação linear é essencialmente o mesmo para solucionar problemas com o objetivo
de minimizar ou maximizar a função objetivo. Primeiramente se utilizam as restrições para determinar a região viável (área de possibilidades).
Em segundo plano, determinam-se os valores das
variáveis de decisão em cada ponto onde as retas de
restrição se cruzam. E, finalmente, com base nos pares
de dados, determinam-se os valores da função objetivo, e seleciona-se a combinação que otimiza (isto é,
minimizando ou maximizando) esta função.
Na programação linear o método gráfico pode ser
usado para qualquer problema com duas variáveis de
decisão. A programação linear é uma técnica poderosa
para a solução de problemas de alocação de recursos
limitados a atividades em competição, bem como com
outros problemas que tenham uma formulação matemática similar. Esta técnica se tornou um instrumento-padrão de grande importância para inúmeras organizações industriais e de negócios.
Na formulação do modelo deve-se construir uma
representação com a coleta de todos os dados necessários, suficientemente minucioso para captar os elementos essenciais que fornecerão resultados compatíveis com a realidade do problema.
O objetivo do estudo de programação linear não
é o equipamento utilizado, nem a predisposição dos
participantes, nem as propriedades físicas do produto
final, mas a combinação de todos os fatores em conjunto, considerados como um processo econômico.
A programação linear tem como objetivo principal a elaboração de uma estratégia dirigida à regulação
dos resultados potenciais de operações futuras através da construção de modelos científicos da situação
aplicada a particulares mecanismos transformadores
de valores nos quais atuam homens, equipamentos e
meios.
A contribuição deste artigo no âmbito empresarial torna-se evidente que a prática específica da
Programação Linear, é uma importante ferramenta
gerencial para a escolha das melhores decisões. Como
sugestão de pesquisas futuras, tem-se a aplicação de
outras técnicas como a simulação para analisar o processo produtivo e verificar outras possibilidades de
melhoria nos processos.
REFERÊNCIAS BIBLIOGRÁFICAS
ANDRADE, E. L. Introdução à pesquisa operacional: métodos e modelos para análise de decisões. 4 ed.
Rio de Janeiro: LTC, 2009.
BRONSON, R. Pesquisa operacional. São Paulo: McGraw-Hill, 1985.
ELLENRIEDER, A. Pesquisa operacional. Rio de Janeiro: Almeida Neves Editores Ltda., 1971.
BARBOSA • Utilização da programação linear
HILLIER, F. S. LIEBERMAN, G. J. Introdução à pesquisa operacional. 9 ed. Porto Alegre : McGraw-Hill, 2013.
LACHTERMACHER, G. Pesquisa operacional na tomada de decisões. 4 ed. Rio de Janeiro: Campus, 2009.
LOESCH, C.; HEIN, N. Pesquisa operacional: fundamentos e modelos. São Paulo: Saraiva, 2009.
MOREIRA, D. A. Pesquisa operacional: curso introdutório. 2. ed. São Paulo: Cengage Learning, 2010.
PASSOS, E. J. P. F. Programação linear como instrumento da pesquisa operacional. São Paulo: Atlas, 2008.
SILVA, E. M. et. ali. Pesquisa operacional: para os
cursos de administração e engenharia. 4. ed. São Paulo: Atlas, 2010.
WAGNER, H. M. Pesquisa operacional. 2. Ed. Rio de
Janeiro: Prentice-Hall, 1986.