resolução pelo método gráfico

PESQUISA OPERACIONAL
RESOLUÇÃO PELO MÉTODO GRÁFICO
No exemplo há duas variáveis básicas: ST e LX . Serão agora representadas, em um
gráfico bidirecional, tanto as restrições como a função objetivo.
O modelo é:
Maximizar:
Sujeito a:
Lucro = 30 x ST + 40 x LX
ST
24
LX
16
1 x ST + 2 x LX
40
PLOTANDO AS RESTRIÇÕES
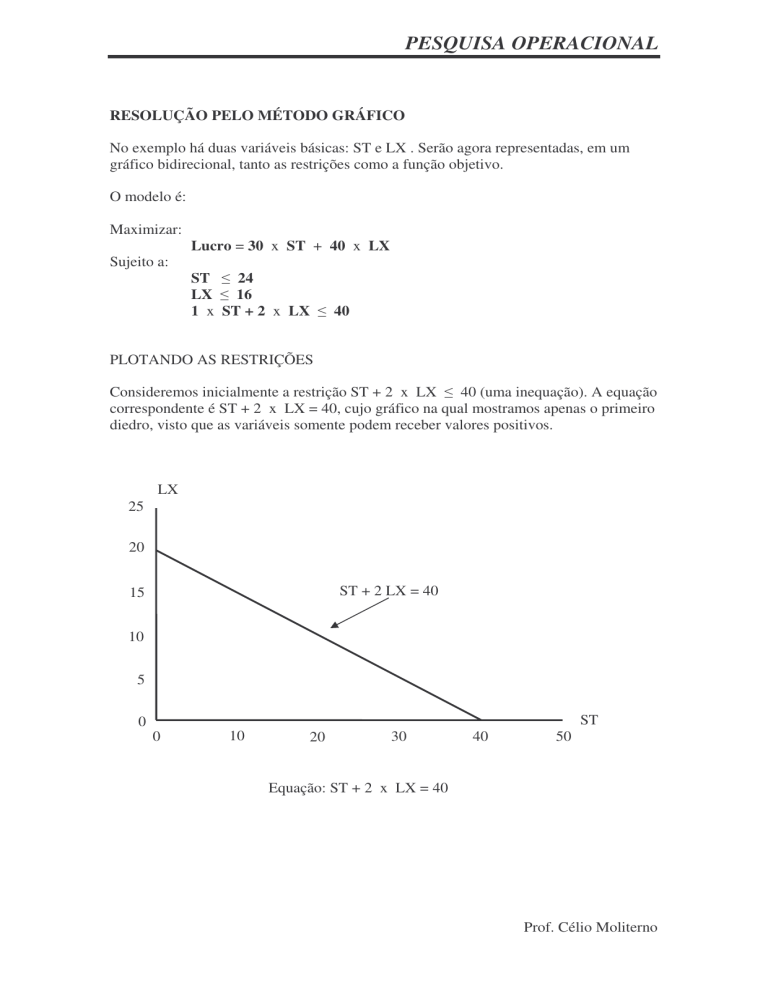
Consideremos inicialmente a restrição ST + 2 x LX
40 (uma inequação). A equação
correspondente é ST + 2 x LX = 40, cujo gráfico na qual mostramos apenas o primeiro
diedro, visto que as variáveis somente podem receber valores positivos.
25
LX
20
ST + 2 LX = 40
15
10
5
0
0
10
20
30
40
50
ST
Equação: ST + 2 x LX = 40
Prof. Célio Moliterno
PESQUISA OPERACIONAL
LX
25
20
15
10
ST + 2 LX < 40
5
0
0
10
30
20
Inequação: ST + 2 x LX
40
50
ST
40
N a Geometria Analítica, representamos um ponto de um gráfico por (x,y) e, no
presente gráfico, cada ponto do segmento de reta traçado representa um par de produto
(Standard, Luxo) que utiliza exatamente 40 operários. Visto que nossa inequação prevê
que podemos utilizar até 40 operários, podemos concluir que a região positiva abaixo do
segmento de reta traçado contém os pontos, ou melhor, os pares de produção (Standard,
Luxo) que, juntamente com os pontos de segmento de reta, atendem corretamente à
inequação. No Gráfico acima mostramos esta conclusão. Utilizando o mesmo
raciocínio, mostramos os Gráficos abaixo, para as restrições ST
24 e LX
16,
respectivamente.
LX
25
ST = 24
24RR242
20
15
10
ST < 24
5
0
ST
0
5
15
10
A Restrição ST
25
30
24
Prof. Célio Moliterno
PESQUISA OPERACIONAL
25
20
LX = 16
15
10
LX < 16
5
0
ST
10
0
30
20
A Restrição LX
40
ST
50
16
A REGIÃO DE SOLUÇÕES POSSÍVEIS
Colocando todas as restrições em um único gráfico, ele toma o formato do Gráfico
abaixo, na qual a interseção entre todas as restrições produziu a região hachurada. Seus
pontos representam pares de produção (Standard, Luxo) que atendem a todas as
restrições e, obviamente, qualquer ponto fora desta região não atende a todas as
restrições. Uma região como esta recebe em Geometria o nome de região convexa
simplex. Portanto, nosso problema pode ser compreendido como sendo o de procurar
qual ponto da região simplex fornece o maior valor para o lucro.
25
LX
20
15
10
Região Simplex
5
0
0
5
10
15
25
30
ST
Prof. Célio Moliterno
PESQUISA OPERACIONAL
PLOTANDO A FUNÇÃO OBJETIVO
A função objetivo Lucro = 30ST + 40LX pode ser transformada em:
3
Lucro
LX = − ST +
4
40
Em um diedro (ST, LX), esta equação representa um família de retas de parâmetro
Lucro/40, ou seja, para cada valor de Lucro temos uma reta diferente. Ademais, todas as
retas são paralelas entre si, pois possuem o mesmo coeficiente angular -3/4. No Gráfico
abaixo temos algumas retas desta família, em que cada uma foi obtida dando-se um
valor para o lucro. Portanto, qualquer ponto de uma mesma reta possui pontos ou pares
de produção (Standard, Luxo) que fornecem o mesmo lucro. Esta família de retas é
conhecida por retas iso-lucro.
25
Solução Ótima
ST = 24
LX = 8
Lucro = R$ 1.040,00
LX
L = 800
20
15
10
L = 1.200
5
0
L = 1.040
0
5
10
15
25
30
ST
Visualmente podemos observar que, quanto mais afastada da origem está uma destas
retas, maior o valor do Lucro correspondente. Isto pode ser demonstrado facilmente
analisando a equação em questão LX = -3/4ST + Lucro/40 semelhante á equação da
reta y = ax + b, onde:
a = -3/4 (coeficiente angular)
b = Lucro/40 (coeficiente linear)
Na equação da reta, o termo b representa o ponto de interseção da reta com o eixo y.
Considerando uma família de retas paralelas entre si, quanto mais distante da origem
está uma reta, maior o Lucro, maior será b e mais distante estará a reta da origem.
Prof. Célio Moliterno
PESQUISA OPERACIONAL
PROGRAMAÇÃO LINEAR:
FORMA NORMAL
Condições de não negatividade
Toda variável ainda não restrita a ser não negativa é substituída pela diferença de duas
novas variáveis não negativas.
As restrições lineares são da forma
n
j =1
a x
ij
j
~
b
i
onde ~ indica uma das relações , , = (não necessariamente a mesma para cada i). As
constantes b1 podem ser consideradas sempre não negativas.
Exemplo – A restrição 2x1 – 3x2 + 4x3 -5 é multiplicada por – 1 a fim de obter
-2x1 + 3x2 - 4x3 5, no qual o elemento do lado direito da relação é não negativo.
VARIÁVEIS DE FOLGA E VARIÁVEIS DE EXCESSO
Uma restrição linear de forma
a x
ij
j
≤
b
i
pode ser convertida em igualdade
pela adição de uma nova variável não negativa ao lado esquerdo da desigualdade. Tal
variável é numericamente igual à diferença entre os valores e à esquerda da
desigualdade e é conhecida como variável de folga. Ela representa o desperdício
acarretado pela parte do sistema modelada pela restrição em pauta.
Exemplo – A restrição 4x1 + 5x2 + 3x3 + 5x4
30 000
4x1 + 5x2 + 3x3 + 5x4 + x5 = 30 000
Uma restrição linear de forma
a x
ij
j
≥
b
i
pode ser convertida em igualdade
subtraindo-se ao lado esquerdo da desigualdade uma nova variável, não negativa. Tal
variável é numericamente igual à diferença entre os valores e à esquerda e a direita da
desigualdade e é conhecida como variável de excesso. Ela representa um excesso das
variáveis de entrada nesta parte do sistema modelada pela restrição em pauta.
Exemplo – A restrição 4x1 + 5x2 + 3x3 + 5x4
30 000
4x1 + 5x2 + 3x3 + 5x4 - x5 = 30 000
Prof. Célio Moliterno
PESQUISA OPERACIONAL
GERAÇÃO DE SOLUÇÃO INICIAL VIÁVEL
•
•
•
Condição de não negatividade para as restrições
Transformar todas as restrições lineares em igualdades
(introduzir variáveis de Folga e de Excesso onde necessário)
Adicionar uma nova variável, chamada variável artificial, a esquerda de todas as
restrições que não contenham variável de Folga
Solução inicial não negativa para este novo conjunto de restrições
•
•
As variáveis de Folga e Artificial, devem ser igual ao valor do lado direito da
equação.
Igualar a zero todas as outras variáveis, inclusive as variáveis de excesso.
Exemplo - O conjunto de restrições
x1 + 2x2
3
4x1 + 5x2
6
7x1 + 8x2 = 15
Transformado num sistema de equações adicionando-se a variável de folga x3 no termo
à esquerda da primeira restrição e subtraindo-se a variável de excesso x4 do termo à
esquerda da segunda restrição. O novo sistema é
x1 + 2x2 + x3
= 3
4x1 + 5x2
- x4 = 6
7x1 + 8x2
= 15
Se agora as variáveis artificiais x5 e x6 forem adicionadas respectivamente ao
primeiro membro das duas últimas restrições do sistema de equações que não possuem
variáveis de folga, o resultado será
x1 + 2x2 + x3
4x1 + 5x2
= 3
- x4 + x5
7x1 + 8x2
= 6
+ x6 = 15
Uma solução não negativa correspondente a este último sistema de equações será:
x3 = 3 , x5 = 6 , x6 = 15 e
x1 = x2 = x4 = 0
Prof. Célio Moliterno
PESQUISA OPERACIONAL
Exercícios:
Defina a Solução Inicial Viável para os conjuntos de restrições abaixo:
x1 + 4x2
2
2x1 + 5x2
6
x1 + 2x2 = 8
2x1 + x2
-3
7x1 + 5x2
12
x1 + 2x2
28
2x1 + 2x2
8
x1 + 5x2
10
- x1 + 3x2 = 6
5x1 + 2x2 - 3x3
-7
2x1 - 2x2 + 3x3
8
Prof. Célio Moliterno