Modelos de grafos - Areal Editores, SA

PREPARAR O EXAME NACIONAL
MACS • 10.º e 11.º ANOS
Propostas de resolução – Modelos de grafos
PÁG. 115
1.
1.1. O grafo apresentado é Euleriano pois é conexo e tem todos os vértices de grau par.
1.2. O grafo apresentado é não Euleriano pois tem mais do que dois vértices com grau ímpar.
1.3. O grafo apresentado apenas admite um caminho Euleriano pois tem dois vértices de grau ímpar.
2. Um grafo K 4 possui  4  1!  3  2 1  6 circuitos de Hamilton e possui
6
 3 circuitos diferentes.
2
Um grafo K 9 possui  9  1!  8  7  6  5  4  3  2 1  40 320 circuitos de Hamilton e possui
40 320
 20160 circuitos diferentes. Existe uma diferença substancial do número de circuitos de um
2
grafo K 4 para um grafo K 9
.
3.
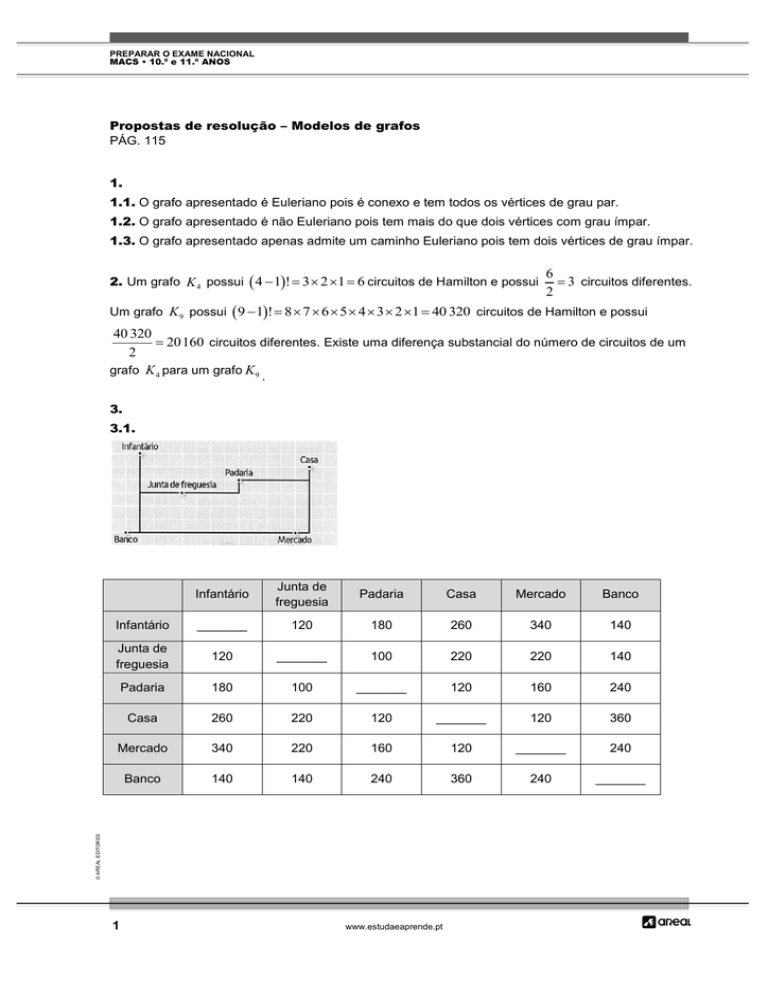
3.1.
Junta de
freguesia
Padaria
Casa
Mercado
Banco
Infantário
_______
120
180
260
340
140
Junta de
freguesia
120
_______
100
220
220
140
Padaria
180
100
_______
120
160
240
Casa
260
220
120
_______
120
360
Mercado
340
220
160
120
_______
240
Banco
140
140
240
360
240
_______
© AREAL EDITORES
Infantário
1
www.estudaeaprende.pt
PREPARAR O EXAME NACIONAL
MACS • 10.º e 11.º ANOS
3.2. Utilizando o Algoritmo da “Cidade mais próxima” temos:
Vértice de partida: Casa
Segundo vértice: Infantário (custo 260)
Vértice mais próximo: Junta de freguesia (custo 120)
Vértice mais próximo: Padaria (custo 100)
Vértice mais próximo: Mercado (custo 160)
Vértice mais próximo: Banco (custo 240)
Regressamos ao vértice de partida: Casa (custo 360)
Circuito:
Casa  Infantário  Junta de freguesia  Padaria  Mercado  Banco  Casa
A Sra. Maria percorreu 260 + 120 + 100 + 160 + 240 + 360 = 1240 metros.
3.3. Utilizando o Algoritmo da “Cidade mais próxima” temos:
Vértice de partida: Casa
Vértice mais próximo: Padaria (custo 120)
Vértice mais próximo: Junta de freguesia (custo 100)
Vértice mais próximo: Banco (custo 140)
Vértice mais próximo: Mercado (custo 240)
Regressamos ao vértice de partida: Casa (custo 120)
Circuito:
Casa  Padaria  Junta de freguesia  Banco  Mercado  Casa
A Sra. Maria percorreu 120 + 100 + 140 + 240 + 120 = 720 metros.
4.
4.1. Não é uma árvore pois existem pares de vértices entre os quais existem mais do que um
caminho e as arestas não são pontes.
4.2. Não é uma árvore pois as arestas não são pontes.
4.3. É uma árvore pois é conexo, existe sempre um só caminho entre qualquer par de vértices e
cada aresta é uma ponte (tem 7 vértices e 6 arestas).
© AREAL EDITORES
5.
5.1. Sim, o grafo é conexo porque não existem vértices nem arestas isolados. Sim é possível, existe
apenas um caminho entre cada par de vértices.
5.2. Entre B e H existe apenas um caminho. Podemos concluir que estamos perante uma árvore.
5.3. Como estamos perante uma árvore, todas as arestas são pontes.
Assim, temos 8 arestas (e 9 vértices).
2
www.estudaeaprende.pt
PREPARAR O EXAME NACIONAL
MACS • 10.º e 11.º ANOS
6.
6.1.
6.2.
7. Utilizando o algoritmos do “Peso das arestas” temos:
Ordenação das arestas pelo seu peso:
FE  5; ED  7; DC  9; CE  10; AB  11; FC  12; BC  14; AF  15
Arestas com menor peso: FE e ED
Aresta com menor peso seguinte: DC (é valida pois não fecha o circuito)
Aresta com menor peso seguinte: CE (não é valida pois fecha o circuito)
Aresta com menor peso seguinte: AB (é valida pois não fecha o circuito)
Aresta com menor peso seguinte: FC (não é valida pois fecha o circuito)
Aresta com menor peso seguinte: BC (é valida pois não fecha o circuito)
A última aresta é AF, fechando o circuito eléctrico.
Ordenando o circuito e considerando A como ponto de partida, temos: ABCDEFA.
© AREAL EDITORES
O custo mínimo será de (11 + 14 + 9 + 7 + 5 + 15)  2,50 = 152,50 €
3
www.estudaeaprende.pt