0.1 Colisões Força impulsiva θi θf pi pf Colisões unidimensionais

0.1 Colisões
1
0.1 Colisões
Força impulsiva
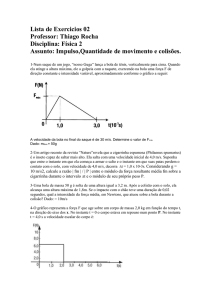
1. Uma pequena esfera de massa m colide com uma parede plana e lisa, de modo que a
força exercida pela parede sobre ela é normal à superfície da parede durante toda a colisão.
Considere que a força resultante sobre a esfera seja apenas a força exercida pela parede. O
ângulo entre o momento linear da esfera antes da colisão (~pi ) e a direção normal à parede
é θi = 45o . Seja θf o ângulo entre o momento linear da esfera depois da colisão (~pf ) e a
direção normal à parede (veja a figura). Sabe-se, ainda, que o módulo da velocidade da
p
esfera após a colisão é 2/3 vi , onde vi é o módulo de sua velocidade antes da colisão.
θi
θf
p~f
p~i
(a) Calcule as razões |~pf |/|~pi | e Kf /Ki , onde Kf e Ki são, respectivamente, as energias
cinéticas da esfera depois e antes da colisão;
(b) A componente do momento linear da esfera perpendicular à parede é conservada
durante a colisão? E a componente paralela? Justifique;
(c) Determine o ângulo θf .
Colisões unidimensionais
2. Uma bolinha de massa m1 colide frontalmente com uma outra, de massa m2 , que está
inicialmente em repouso. A colisão, considerada perfeitamente elástica, ocorre sobre a
superfície de uma mesa sem atrito.
(a) Determine a fração ∆E/E0 em termos de m1 e m2 , onde ∆E é a variação da energia
mecânica da esfera de massa m1 e E0 é sua energia mecânica inicial.
0.1 Colisões
2
(b) Determine a razão m1 /m2 para a qual a perda de energia mecânica da esfera incidente nesta colisão é igual à metade de sua energia mecânica inicial.
3. Considere dois pequenos blocos alinhados sobre o eixo OX . Inicialmente, o bloco da
esquerda, de massa m, tem velocidade v0 ı̂, v0 > 0, enquanto o bloco da direita, de massa
3m, está em repouso, como indica a figura. Grudada no lado esquerdo desse último
bloco há uma mola ideal cujo extremo esquerdo possui um anteparo vertical de massa
desprezível. O bloco de massa m se choca com a mola do bloco da direita fazendo com
que ela se comprima até um certo ponto e depois volte a se distender. Suponha que todos
os movimentos se processem no eixo OX , que a mola permaneça sempre na direção desse
eixo e despreze qualquer tipo de atrito e resistência do ar.
m
v0
3m
O
(a) A componente ao longo do eixo OX do momento linear total do sistema formado
pelos dois blocos e a mola se conserva durante a colisão? E a energia mecânica do
sistema? Justifique.
(b) Determine a velocidade do centro de massa do sistema no instante de maior aproximação entre os blocos.
(c) Calcule de quanto a mola está comprimida no instante de maior aproximação entre
os blocos.
4. Considere três pequenos blocos alinhados sobre o eixo OX . Inicialmente, o bloco da
esquerda, de massa m, está em repouso, o bloco do centro, também de massa m, tem
velocidade v0 ı̂, v0 > 0, e o bloco da direita, de massa M , está em repouso. Grudada
no lado esquerdo desse último bloco há uma mola ideal, cujo extremo esquerdo possui
um anteparo vertical de massa desprezível com o qual o bloco do centro irá se chocar.
Observe que o bloco do centro não ficará preso à mola podendo, inclusive, mudar o
X
0.1 Colisões
3
sentido de seu movimento, dependendo da relação entre m e M . Considere, além disso,
que todos os movimentos se processam no eixo OX , que a mola permaneça sempre na
direção desse eixo e que as únicas forças ao longo de OX sejam as forças de interação
dos blocos entre si e com a mola.
m
m
M
v0
X
O
(a) Qual é a condição entre m e M para que o bloco do centro venha a se chocar com o
bloco da esquerda?
(b) Suponha que tal condição seja satisfeita e que, ao se chocar com o bloco da esquerda, o bloco do centro fique grudado nele. Qual deve ser o valor de M para que
o sistema formado pelos blocos da esquerda e do centro se movam, juntos, com uma
velocidade igual a −(v0 /4)ı̂?
(c) Na situação do item anterior, determine a velocidade final do bloco da direita.
5. Suponha que um pequeno bloco de massa m incida com velocidade de módulo v1i sobre
um outro, de massa M , no qual está presa uma mola ideal de constante elástica k. Antes
da colisão, o bloco de massa M está em repouso e a mola, com seu comprimento natural.
O
m
~v1i
k
M
X
Despreze o atrito entre os blocos e a superfície. Num dado instante, a compressão da
mola será máxima. Durante todo o processo a mola permanece na horizontal. Calcule,
nesse instante, as velocidades dos blocos e a compressão máxima da mola ∆xmax .
6. Dois blocos A e B de massas iguais a ma e mb estão em repouso sobre uma superfície
horizontal sem atrito e mantêm entre eles uma mola comprimida com o auxílio de um
0.1 Colisões
4
A
B
C
fio ideal. Um terceiro bloco, C, de massa mc , está parado à direita de B. Essa situação
inicial do sistema de três blocos está representada na figura abaixo.
O fio que mantém a mola comprimida é cortado. No instante em que a mola volta a ter o
seu tamanho natural (instante em que perde o contato com os blocos), o bloco A tem uma
velocidade para a esquerda de módulo va . O bloco B colidirá, então, com o bloco C.
(a) Determine a velocidade do bloco B logo antes da colisão com o bloco C.
(b) Qual é a energia potencial elástica da mola antes do corte do fio?
(c) Supondo que o bloco B permaneça grudado com o bloco C após colidir com ele,
determine a velocidade do conjunto B + C após a colisão.
(d) Usando explicitamente o resultado do item anterior, determine a velocidade do centro de massa do sistema formado pelos três blocos. Interprete o resultado.
(e) Determine a perda de energia ocorrida na colisão de B com C.
7. Dois blocos de massas M1 e M2 estão, inicialmente, em repouso sobre uma superfície
horizontal lisa. Uma pequeno projétil de massa m é disparado de uma arma com uma velocidade horizontal de módulo v0 e atinge o bloco de massa M1 . Ele atravessa totalmente
esse bloco e atinge o segundo bloco, ficando preso dentro dele. Como a velocidade inicial
do projétil é muito grande, suponha que ele se movimente sempre numa reta horizontal.
Na situação final, o bloco de massa M1 tem velocidade de módulo v1 e o bloco de massa
m2 com o projétil em seu interior tem velocidade de módulo v2 , com v2 > v1 .
A figura ilustra as situações em um instante antes da bala atingir o primeiro bloco, em um
instante depois de passar pelo primeiro e antes de atingir o segundo, e em um instante depois de incrustar no segundo. Considerando como dados as massas M1 e M2 dos blocos,
a massa m da bala, e as velocidades finais v1 e v2 dos blocos, calcule
0.1 Colisões
5
v0
m
M1
M2
v1
v0′
v1
v2
(a) a velocidade inicial v0 da bala ao atingir o primeiro bloco e a velocidade v0′ com que
ela emerge dele,
(b) a velocidade do centro de massa do sistema formado pelo projétil e pelos dois blocos: (i) antes que ele atinja o primeiro bloco e (ii) depois que ele ficou preso no
interior do segundo bloco. Explique a relação entre os resultados obtidos.
Colisões em mais dimensões
8. Uma pequena esfera de dimensões desprezíveis, de massa m e velocidade de módulo
v1i = 3m/s (esfera 1), colide com uma outra, também de dimensões desprezíveis e de
massa 2m, que está inicialmente em repouso (esfera 2). Considere eixos coordenados
OX Y de modo que o eixo OX esteja na direção e no sentido da velocidade da esfera
incidente. Escolha a origem O na posição onde ocorre a colisão entre as esferas e o
instante t = 0 como aquele em que ocorre a colisão (como de costuem, estamos supondo
que o tempo de colisão seja desprezível). No instante tb = 2 s verifica-se que a esfera
incidente se encontra na posição ~r1b = −3 m ̂.
(a) Determine a velocidade do centro de massa do sistema formado pelas duas esferas
antes da colisão. Determine a posição do centro de massa no instante tb .
(b) Determine as velocidades das duas esferas após a colisão e o ângulo θ que a trajetória
0.1 Colisões
6
da esfera de massa 2m faz com o eixo OX . Faça um desenho esquemático da colisão
indicando as posições e as velocidades das duas esferas nos instantes ta = −1 e
tb = 1. Indique, ainda, as posições do centro de massa nesses dois instantes.
(c) Determine a posição da esfera 2 no instante tb . A partir desses resultados verifique
que as duas esferas e o centro de massa estão sobre uma mesma reta, como esperado.
(d) Calcule a variação de energia cinética dessa colisão supondo que m = (1/9) kg.
9. Considere a seguinte colisão entre duas pequenas esferas de mesma massa. Antes do
choque, elas possuem as velocidades ~v1 = v0 ı̂ e ~v2 = v0 ̂, respectivamente, onde v0 é
uma constante positiva. Após a colisão, elas permanecem grudadas uma na outra com
velocidade ~vf . Suponha que a resultante das forças sobre cada uma delas é sempre nula,
exceto durante a colisão, quando as forças de contato são diferentes de zero.
(a) Calcule o módulo de ~vf e o ângulo entre ~vf e eixo OX .
(b) Calcule a variação da energia cinética nessa colisão.