Solução

www.fisicaexe.com.br
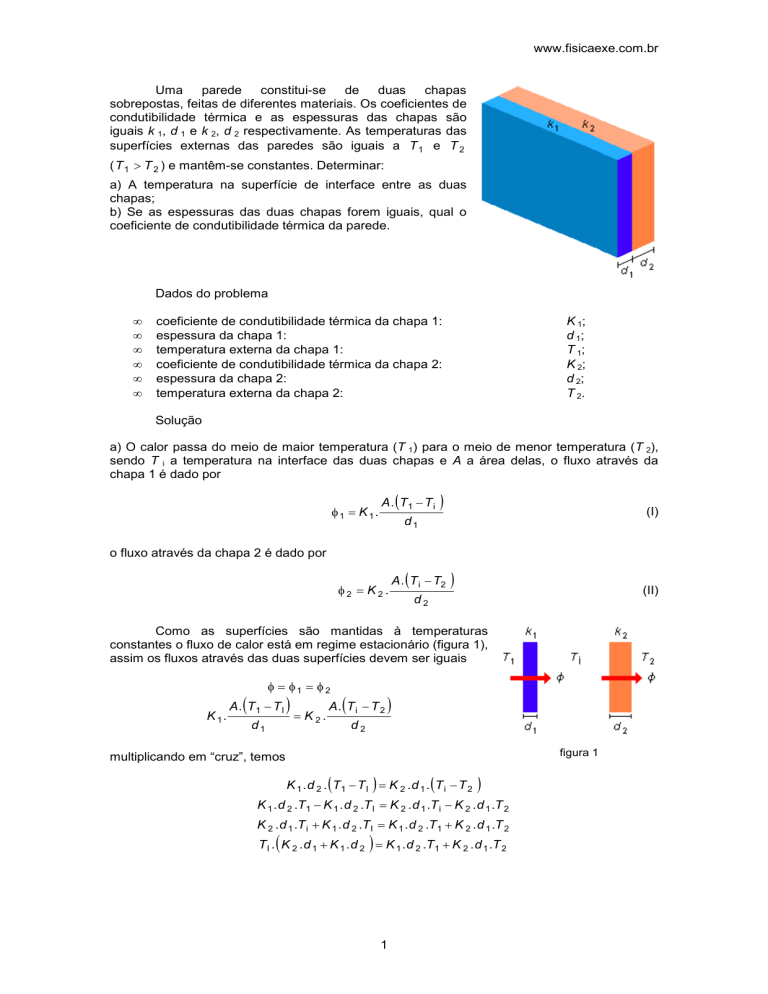
Uma parede constitui-se de duas chapas
sobrepostas, feitas de diferentes materiais. Os coeficientes de
condutibilidade térmica e as espessuras das chapas são
iguais k 1, d 1 e k 2, d 2 respectivamente. As temperaturas das
superfícies externas das paredes são iguais a T 1 e T 2
( T 1 > T 2 ) e mantêm-se constantes. Determinar:
a) A temperatura na superfície de interface entre as duas
chapas;
b) Se as espessuras das duas chapas forem iguais, qual o
coeficiente de condutibilidade térmica da parede.
Dados do problema
•
•
•
•
•
•
K 1;
d 1;
T 1;
K 2;
d 2;
T 2.
coeficiente de condutibilidade térmica da chapa 1:
espessura da chapa 1:
temperatura externa da chapa 1:
coeficiente de condutibilidade térmica da chapa 2:
espessura da chapa 2:
temperatura externa da chapa 2:
Solução
a) O calor passa do meio de maior temperatura (T 1) para o meio de menor temperatura (T 2),
sendo T i a temperatura na interface das duas chapas e A a área delas, o fluxo através da
chapa 1 é dado por
φ1 = K 1.
(
A . T1 − T i
)
(I)
d1
o fluxo através da chapa 2 é dado por
φ2 = K2.
(
A . T i − T2
)
(II)
d2
Como as superfícies são mantidas à temperaturas
constantes o fluxo de calor está em regime estacionário (figura 1),
assim os fluxos através das duas superfícies devem ser iguais
K 1.
φ = φ1 = φ 2
(
A. T1 − T I
d1
)=K
2.
(
A. T i − T 2
)
d2
figura 1
multiplicando em “cruz”, temos
(
)
(
K 1 . d 2 . T1 − T I = K 2 .d 1 . T i − T 2
)
K 1 . d 2 .T 1 − K 1 . d 2 .T I = K 2 . d 1 .T i − K 2 . d 1 .T 2
K 2 . d 1 .T i + K 1 . d 2 .T I = K 1 . d 2 .T 1 + K 2 . d 1 .T 2
(
)
T I . K 2 . d 1 + K 1 . d 2 = K 1 . d 2 .T 1 + K 2 . d 1 .T 2
1
www.fisicaexe.com.br
TI =
K 1 . d 2 .T 1 + K 2 . d 1 .T 2
K 2 .d 1 + K 1 .d 2
b) Para espessuras iguais (d 1 = d 2 = d) a expressão obtida no item anterior para a temperatura
na interface se reduz a
TI =
K 1 . d .T 1 + K 2 . d .T 2
K 2 .d + K 1 .d
colocando a espessura d em evidência no numerador e no denominador, temos
TI =
(
d . K 1 .T 1 + K 2 .T 2
(
d. K 2 + K1
TI =
)
)
K 1 .T 1 + K 2 .T 2
(III)
K 2 + K1
substituindo (III) em (I) e d = d 1, obtemos

K 1 .T 1 + K 2 .T 2
A . T1 −

K 2 + K1
φ1 = K 1. 
d




colocando os termos entre parênteses no mesmo denominador (K 2 + K 1), escrevemos
(
)
 T 1 . K 2 + K 1 − K 1 .T 1 − K 2 .T 2 

A.


K 2 + K1


φ1 = K 1.
d
A  K 2 .T 1 + K 1 .T 1 − K 1 .T 1 − K 2 .T 2 
φ 1 = K 1 . .

d 
K 2 + K1

A  T 1 . K 2 − K 2 .T 2 
φ 1 = K 1 . .

d 
K 2 + K1

colocando o termo
K2
K 2 + K1
em evidência
φ1 =
K 1 .K 2
K1 + K 2
.
(
A . T1 − T 2
)
(IV)
d
A espessura total será de 2 d (figura 2) e sendo K o coeficiente de
condutibilidade térmica do conjunto o fluxo de calor através da parede como
um todo pode ser escrito como
φ = K.
(
A. T1 − T i
)
2d
(V)
Como o regime de fluxo é estacionário as expressões (IV) e (V) deve
ser iguais
2
figura 2
www.fisicaexe.com.br
K.
(
)=
A . T1 − T i
2d
φ = φ1
K 1 .K 2
K1 + K 2
.
(
A. T1 − T 2
)
d
K 1 .K 2
K
=
2 K1 + K 2
K =
2 K 1 .K 2
K1 + K 2
observação: poderíamos substituir a expressão (III) em (II), o que nos levaria a
 K 1 .T 1 + K 2 .T 2
A.
−T2

K 2 + K1

φ2 = K2.
d1




colocando os termos entre parênteses no mesmo denominador (K 2 + K 1), escrevemos
(
)
 K 1 .T 1 + K 2 .T 2 − T 2 . K 2 + K 1 

A.


K 2 + K1


φ2 = K2.
d
A  K 1 .T 1 + K 2 .T 2 − K 2 .T 2 − K 1 .T 2 
φ 2 = K 2 . .

d 
K 2 + K1

φ2 = K 2.
colocando o termo
K1
K 2 + K1
A  K 1 .T 1 − K 1 .T 2
.
d 
K 2 + K1




em evidência
φ2 =
K 1 .K 2
K1 + K 2
.
(
A. T1 − T 2
)
d
Este resultado é equivalente a expressão (IV) encontrada acima.
3