inf.unioeste.br

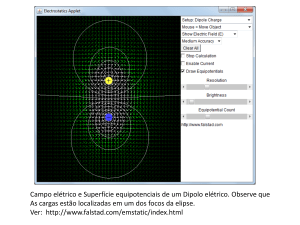
Capítulo 23 –
Potencial Elétrico
1
Energia Potencial
Trabalho e energia…
b 

Wa → b = ∫ F ⋅ ds = − ∆ U
a
Energia Potencial Elétrica
Unidade de Medida  joule (J)

E
Para duas cargas pontuais :
Wr1 → r2 =
rb
∫
ra
kq0 q
kq0 q kq0 q
dr =
−
2
r
rb
ra
 kq0 q kq0 q 
− ∆ U = − (U b − U a ) = − 
−

r
r
a
 b

kq0 q
kq0 q
Ub =
ou U a =
Então
rb
ra
U12
kq1q2
= −
r
b
q0
r
b
ra
a
r
q
2
Potencial ou Voltagem

Potencial Elétrico é a energia potencial por unidade de
carga
U12
V1 =
q2


Unidade de Voltagem: Volts (V)= Joule/Coulomb (J/C)
Lembrando que a unidade de campo elétrico E é N/C
N  N  J  V ⋅ C 
V
1 =  

=1
C  C  N ⋅ m J 
m

Temos uma nova unidade para o campo elétrico: V/m
 O campo elétrico deve estar relacionado com a
voltagem!
3
Lembrando que:
F12
F12 = E1 ⋅ q2 ou E1 =
q2
Vetorial
Temos a analogia :
U12
U12 = V1 ⋅ q2 ou V1 =
q2
Escalar
4
Diferença de potencial (ou o que se
mede com um voltímetro!)
Tomando WP1 → P2 =
r2
∫


F12 ⋅ ds = − ∆ U
r1
e dividindo por q 2 :
WP1 → P2 =
r2
∫


F12 ⋅ ds = − ∆ U
r1
q2
=
WP1 → P2
q2
=
r2
∫
 
E ⋅ ds = − ∆ V
r1
r2
 
∆ V = − ∫ E ⋅ ds
r1
Diferença de potencial entre os
5
Como calcular V
kqq2
U
kq
r
V=
=
=
q2
q2
r
V=
∑
kqi
ri
∫
k dq
r
i
V=
Carga pontual (o sinal de q
deve ser levado em conta!)
Conjunto de Cargas
Distribuição contínua de cargas
O potencial exige um referencial definido!
6
Exemplo
Na figura abaixo, o ponto P está no centro do retângulo.
Tomando V=0 no infinito, qual é o potencial total em P,
devido às seis partículas (pontuais) carregadas?
+5q
d
-2q
d
+3q
d
d
P
d
-2q
-3q
d
+5q
7
Encontramos a distância do centro aos vértices:
d
+5q
d
-2q
s
d/2
d
+3q
d
P
d
-3q
d
d
-2q
+5q
8
Potencial (Voltagem) é um escalar e pode ser
somado diretamente, mas levando em conta o
sinal das cargas!
5q
V3 = k
s
2
3
d
+5q
V2 = k
d
3q
V4 = k
s
-2q
− 2q
d
2
d
+3q
4
− 2q
d
2
5
∑
i
− 3q
V1 = k
s
s
d/2
-2q
-3q
d
P
V5 = k
V=
1
d
d
d
+5q
5q
V6 = k
s
6
Vi = V1 + V2 + V3 + V4 + V5 + V6
9
V=
∑
Vi = V1 + V2 + V3 + V4 + V5 + V6
i
V = V1 + V2 + V3 + V4 + V5 + V6
V=
V=
V=
V=
 − 3q − 2q 5q 3q − 2q 5q 

k
+
+
+
+
+
 s
d
d
s
s
s 
2
2


 − 4q 10q 

k
+
 d
s 
 2

kq
4 5− 8
d
0.94kq
d
(
)
10
Superfícies equipotenciais
Linhas do Campo E
kq/r1
ΔV = V2 − V1
q
kq/r2
 1 1
V2 − V1 = k ⋅ q ⋅  − 
 r2 r1 
As linhas do campo elétrico são perpendiculares às superfícies
equipotenciais.
11
Superfícies equipotenciais
+++++++++++++ +++++++ +++++++
V1
d
Linhas do
Campo E
Equipotenciais
V2
-----------------------------
ΔV = V2 − V1
V2 − V1 = E ⋅ d
As linhas do campo elétrico são perpendiculares às superfícies
equipotenciais.
12