Potencial Elétrico

Potencial Elétrico
Objetivos:
●
Explorar o Potencial Elétrico de cargas pontuais e
distribuições contínuas de cargas.
Sobre a Apresentação
Todas as gravuras, senão a maioria, são dos livros:
●
●
●
Sears & Zemansky, University Physics with Modern Physics – ed.
Pearson, 13a edition
Wolfgang Bauer and Gary D. Westfall, University Physics with
Modern Physics – ed. Mc Graw Hill, Michigan State University, 1a
edition
Halliday & Resnick, Fundamentals of Physics, 9a edition.
Potencial de uma
Carga Pontual
Voltando à expressão do potencial elétrico:
onde a força elétrica em um caso qualquer será:
Substituindo na expressão acima, e escolhendo um caminho qualquer para a
integral, teremos:
em seguida divida a expressão pela carga teste q0,
Potencial de uma
Carga Pontual
O Campo Elétrico de uma carga puntiforme q é dado por:
Portanto o Potencial Elétrico gerado por esta carga será:
Potencial de uma
Carga Pontual
Se tomarmos o ponto inicial no infinito como potencial nulo, o potencial em
uma distância r de q será:
Que seria o mesmo se tomássemos a energia potencial de uma carga
puntiforme por uma carga teste q0:
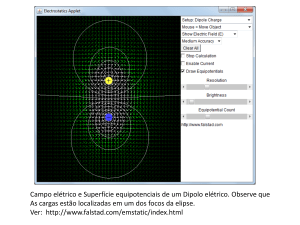
Superfícies Equipotenciais
Observe que o Potencial Elétrico de uma carga pontual depende apenas da
distância radial da carga, r. Isto significa que para um raio fixo, o seu
potencial elétrico é constante.
Estas curvas circulares em torno da carga são chamadas de Superfícies
Equipotenciais, pois não há variação de potencial elétrico quando uma carga
se desloca sobre elas.
Superfícies Equipotenciais
Estas curvas circulares em torno da carga são chamadas de Superfícies
Equipotenciais, pois não há variação de potencial elétrico quando uma carga
se desloca sobre elas.
Estas curvas são cortes transversais das superfícies de esferas concêntricas
na carga em questão. Dai o nome superfícies.
Superfícies Equipotenciais
Observe que o movimento da carga testes q0 sobre os caminhos A e B não
realizam trabalho, uma vez que estes estão sobre a mesma superfície
equipotencial.
q0
+
A
q0
+
+
B
+
Observe também que o campo elétrico é sempre ortogonal à superfície
equipotencial, o que significa que um deslocamento sobre estas superfícies,
a força será sempre ortogonal ao deslocamento, resultando em trabalho
nulo.
Superfícies Equipotenciais
Nos caminhos A e B, abaixo, o trabalho realizado também será nulo.
q0
+
A
q0
+
+
B
+
Isto ocorre porque a variação do potencial é nulo no movimento. A
explicação é simples: enquanto se faz trabalho sobre o sistema movendo a
carga teste contra as linhas de campo (armazena energia no campo), esta
energia armazenada é devolvida quando a carga teste se move na direção
das linhas de campo. Desta forma o trabalho total será nulo.
Superfícies Equipotenciais
As figuras a seguir mostram um corte transversal das superfícies
equipotenciais para um arranjo de duas cargas de sinais opostos e duas de
mesmo sinal.
Superfícies Equipotenciais
Exemplo: As linhas abaixo representam duas superfícies equipotenciais de
40V e 15V, geradas por uma distribuição de cargas. Uma carga de 5μC é
movida entre as linhas, conforme o tracejado em azul. Determine o trabalho
realizado sobre a carga.
No caminho a, como
a
Já que a carga se move sobre a superfície equipotencial
de 40V.
b
No caminho b:
40V
15V
Portanto a carga recebeu 125μJ de energia, que pode ser transformada em
movimento.
Distribuição Contínua
de Cargas
Exemplo 1: Uma carga Q é distribuída uniformemente em uma haste de
comprimento 2a. Determine o potencial elétrico gerado por esta distribuição
de cargas a uma distância d do centro da haste.
O potencial elétrico gerado pelo elemento de
carga dq é,
com,
portanto,
Distribuição Contínua
de Cargas
Integrando ao longo de todo o fio,
Distribuição Contínua
de Cargas
Exemplo 2: Um disco de raio R possui uma densidade de carga σ,
homogênea. Determine o potencial elétrico gerado pelo disco em um ponto
P, a uma distância z do centro do disco.
Um anel de raio R' e espessura dr gera o potencial,
onde,
portanto,
Distribuição Contínua
de Cargas
integrando em todo o disco,
Potencial Elétrico
Determine o Potencial Elétrico em todo o espaço, de uma esfera condutora
de raio R e carga q.
O Campo Elétrico da esfera foi determinado no
capítulo anterior, como:
Portanto o campo fora da esfera será:
assumindo que o potencial no infinito é nulo.
Potencial Elétrico
Portanto o potencial na superfície da esfera será:
Dentro da esfera condutora o campo é nulo, e portanto o movimento de uma
carga teste no interior da esfera não realiza trabalho. Isto significa que o
potencial no interior da esfera deve ser constante.
Campo a Partir do
Potencial
Imagine uma carga q0 deslocando-se por uma região, como ilustra a figura
abaixo. As linhas tracejadas são superfícies equipotenciais muito próximas
umas das outras. A diferença de potencial entre duas linhas adjacentes pode
ser determinada pela expressão:
onde ds é um deslocamento ao longo da reta s.
Como “E cos θ” é a projeção do campo na direção
da reta s, podemos escrever:
Campo a Partir do
Potencial
“A componente do campo elétrico em uma direção é igual a menos a taxa
com que o potencial elétrico varia com o deslocamento naquela direção.”
Exemplo: O potencial elétrico gerado por um disco metálico de raio R, a um
ponto P a uma distância z do centro do disco foi calculado como:
O campo elétrico gerado em P: