Primeira Lista de Exercícios.

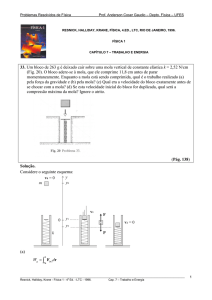
Figure 1: Diagrama esquemático do MHS da partícula do exercício 1.
Primeira Lista de Exercícios.
1. Uma partícula que se move num movimento harmônico simples de período
T
−xm no instante t = 0. Ela estará em −xm ,
xm , em 0, entre 0 e −xm ou entre 0 e xm quando t (a) for 2.00T , (b)
3.5T e (c) for 5.25T [Halliday and Resnick, 1997]?
como o da Figura 1 está em
em
for
2. Deduza a expressão da velocidade de uma oscilação simples a partir da
solução
x = x (t).
x =
3. Deduza a expressão da aceleração de um MHS a partir da solução
xm cos (ωt + φ).
4. Quais das seguintes relações de força produzem oscilações simples:
N
x,
F = 10 m
N 2
−400 m2 x ?
(b)
F = 5N cos (ωt + φ),
m =680g
N
k = 65 m
. O bloco
5. Um bloco cuja massa m é
constante de mola é
(c)
N
F = − 5m
x,
e (d)
(a)
F =
está até ligado a uma mola cuja
é puxado de uma distância x igual
a 11 centímetros a partir de sua posição de equilíbrio em
x = 0 numa
t = 0.
superfície sem atrito e liberado a partir do repouso no instante
(a) Quais são a frequência angular, a frequência e período do movimento
resultante ?
(b) Qual é a amplitude da oscilação?
(c) Qual é a velocidade máxima do bloco oscilante e onde está o bloco
quando ele tem essa velocidade?
(d) Qual é a magnitude
am
da aceleração máxima do bloco?
(e) Qual é a constante de fase do movimento?[Halliday and Resnick,
1997]
1
Figure 2: Diagrama esquemático referente ao exercício 6b
6. Em
t = 0,
x (0) do bloco em um oscilador linear como o
x (0) como x no instante de tempo t = 0.).
v (0) é então -0.920m/s, e sua aceleração a (0) é
o deslocamento
da Figura 2 é -8.50cm (leia
A velocidade do bloco
4.70 sm2 .
ω
(a) Qual é a frequência angular
(b) Qual é a constante de fase
do sistema?
φ
e a amplitude
xm ?
[Halliday and
Resnick, 1997]
7. Na Figura 2, o bloco tem uma energia cinética de 3J e a mola tem uma
energia potencial elástica de 2J quando o bloco está em
(a) Qual é a energia cinética quando o bloco está em
x = +2.0cm.
x = 0?
Qual a
energia potencial quando o bloco está em
(b) (b)
x = −2.0cm
(c) (c)
x = −xm ?
e em
8. Muitos prédios altos têm amortecedores massivos, que são dispositivos que
impedem que estas construções balancem devido a força dos ventos.
O
dispositivo pode ser um bloco preso a extremidade de uma mola, e desliza
sobre uma trilha lubricada. Se o prédio oscila, digamos em direção ao
leste, o bloco também irá se mover para leste, mas atrasado o suciente
para que quando ele nalmente se mova o prédio já está se movendo na
direção oeste.
Assim, o movimento do oscilador está fora de compasso
com o movimento do prédio.
Suponha que o bloco tem uma massa de
m = 2.72 × 105 kg e foi desenhado
10Hz e amplitude x = 20.0cm.
para oscilar com uma frequência
f =
(a) Qual é a energia mecânica total do sistema massa mola?
(b) Qual é a velocidade do bloco quando ele passa pela posição de equilíbrio?[Halliday and Resnick, 1997]
9. A aceleração de uma partícula que se desloca num movimento harmônico
simples ilustrada na Figura 3. .
(a) A qual desses pontos corresponde a posição da partícula em
−xm ?
(b) No ponto 4, a velocidade da partícula é positiva, negativa ou zero?
2
Figure 3: Aceleração em função do tempo referente à questão 9.
Figure 4: Diagrama esquemático do problema 10.
(c) No ponto 5, a partícula está em
entre
−xm
−xm , xm ,
em 0, entre 0 e
xm
ou
e 0?
10. Na Figura 4, um bloco pesando 14.0N, que pode deslizar sem atrito com
um ângulo
θ = 40◦ ,
está conectado ao topo da inclinação por uma mola
sem massa de comprimento natural 0.450m, e constante de mola 120N/m.
(a) Quão longe do topo está a posição de equilíbrio?
(b) Se o bloco for deslocado dessa posição e liberado, qual será a frequência da oscilação?
11. Na Figura 5, dois blocos (m
= 1.8kg e M = 10kg) e uma mola k = 200N/m
estão arranjados em uma superfície horizontal sem atrito. O coeciente de
atrito estático entre os dois blocos é de 0.40. Que amplitude do movimento
harmônico simples desse sistema de duas massas e a mola põe o bloco
menor no limiar do deslizamento sobre o bloco maior?
[Halliday and
Resnick, 1997]
12. Na Figura duas molas estão ligadas e conectadas a um bloco de massa m
= 0.245kg que está oscilando sobre uma superfície sem atrito. As molas
têm cada uma a constante de mola k = 6430N/m. Qual é a frequência
das oscilações? [Halliday and Resnick, 1997]
13. Um bloco de massa
m = 2.0kg
está preso a uma mola como na Figura
13b. . A constante de força da mola é
k = 196N/m.
O bloco é afastado
de 5 centímetros de sua posição de equilíbrio e liberado em
3
t = 0.
Figure 5: Diagrama esquemático do problema 11.
Figure 6: Diagrama esquemático do problema 12
(a) Determine a frequência angular
ω,
a frequência
f
o período
T.
(b) Escreva x como função do tempo..[Tipler and Mosca, 1995]
14. Você está sentado em uma prancha de surf, que sobe e desce ao utuar
sobre algumas ondas. O deslocamento vertical da prancha é dado por:
y = (1.2m) cos
π
1
t+
2.0s
6
.
(a) Determine a amplitude, frequência angular, constante de fase, frequência e o período do movimento.
(b) Onde está a prancha em t = 1.0s?
(c) Determine a velocidade e aceleração como funções do tempo t.
(d) Determine os valores iniciais a posição da velocidade e da aceleração
da prancha.
(e) Determine os valores máximos de velocidade e da aceleração. [Tipler
and Mosca, 1995]
15. A posição de uma partícula é dada por
x = 7.0cm cos(6πt),
com
t
dado
em segundos. Quais são (a) a frequência, (b) o período e (c) a amplitude
Figure 7: Diagrama esquemático do exercício 13b.
4
Figure 8: Diagrama esquemático do exercício 8.
do movimento da partícula? (d) Qual é o primeiro instante, após
t = 0,
em que a partícula estará em sua posição de equilíbrio? Nesse instante em
que sentido estará se movendo?[Tipler and Mosca, 1995]
16. O período de uma partícula oscila em movimento harmônico simples é 8.0s.
Em
x
t = 0,
a partícula está em repouso em x = A = 10cm.
como função de
t.
(a) Esboce
(b) Determine a distância percorrida no primeiro
segundo terceiro e quarto segundos após
t = 0.
Tipler and Mosca [1995]
17. Durante um terremoto,um piso horizontal oscila horizontalmente em um
movimento harmônico simples aproximado.
Suponha que ele oscila em
uma única frequência com 0.8s de período.
(a) Após o terremoto, você
examina o vídeo do piso em movimento e verique que uma caixa sobre
o piso começou a escorregar quando a amplitude da oscilação atingiu 10
centímetros.
De posse desses dados, determine o coeciente de atrito
estático entre a caixa e o piso.
(b) Se o coeciente de atrito entre a
caixa é o piso for 0.40, qual será a amplitude da oscilação antes da caixa
escorregar? [Tipler and Mosca, 1995]
18. A Figura 8 ilustra um sistema massa mola colocado a oscilar num movimento harmônico simples em dois experimentos. No primeiro, o bloco é
empurrado a partir da posição de equilíbrio através de um deslocamento
d1 ,
e então é liberado. No segundo ele é puxado da posição de equilíbrio
através de uma distância
d2 ,
e então é liberado. São a (a) amplitude, (b)
período, (c) frequência, (d) energia cinética máxima, (e) e energia potencial máxima do segundo experimento maiores, menores ou iguais aos do
primeiro?[Tipler and Mosca, 1995]
19. Um corpo de 2,4kg sobre uma superfície horizontal sem atrito, está preso
a uma das extremidades de uma mola horizontal de constante de força
k = 4,5kN/m. A outra extremidade da mola é mantida estacionária. A
mola distendida de 10 centímetros a partir do equilíbrio, e é liberada.
Determine a energia mecânica total do sistema.[Tipler and Mosca, 1995]
20. Determine a energia total de um sistema que consiste de um corpo de
3 quilogramas sobre uma superfície horizontal sem atrito oscilando com
amplitude de 3 centímetros e uma frequência de 2,4 Hertz preso a uma
das extremidades de uma mola horizontal. [Tipler and Mosca, 1995]
5
Figure 9: Diagrama esquemático do problema 25.
21. Um corpo de 1,50kg sobre uma superfície horizontal sem atrito oscila preso
a uma das extremidades de uma mola ( constante de força k = 500N/m). A
rapidez máxima do corpo é de 70,0cm/s. (a) Qual é a energia mecânica total do sistema? (b) Qual é a amplitude do movimento?[Tipler and Mosca,
1995]
22. Um corpo de 3 quilogramas sobre uma superfície horizontal sem atrito
oscila preso a uma das extremidades de uma mola de constante de força
igual a 2,0kN/m com uma energia mecânica total de 0,90J. (a) Qual é
a amplitude do movimento?
(b) qual é a rapidez máxima?[Tipler and
Mosca, 1995]
23. Um corpo sobre uma superfície horizontal sem atrito oscila preso a uma
das extremidades de uma mola com amplitude de 4.5cm.
Sua energia
mecânica total é 1.4J. Qual é a constante de força da mola?[Tipler and
Mosca, 1995]
24. Um corpo de 3,0kg está sobre uma superfície horizontal sem atrito, e o
Silas preso a uma das extremidades de uma mola com uma amplitude de
8,0cm. Sua aceleração máxima é 3.5m/s^2. Determine a energia mecânica
total.[Tipler and Mosca, 1995]
25. Você deve construir o sistema de transferência de oscilação ilustrado na
Figura 9 Ele consiste de dois sistemas massa molas pendurados em um
bastão exível. Quando a mola do sistema 1 é elongada e então liberada,
o movimento harmônico simples resultante do sistema 1 com frequência 1
põe o bastão a vibrar. O bastão exerce então uma força no sistema 2, que
passará a oscilar com a mesma frequência
quatro molas com constantes de mola
quatro blocos com massas
m
k
f1 .
Você pode escolher dentre
de 1600, 1500, 1400, 1200N/m e
de 800, 500, 400 e 200kg.
Determine que
mola deveria ir com que bloco em cada sistema se o objetivo é maximizar
a amplitude da oscilação 2.[Tipler and Mosca, 1995]
26. Na gura , duas molas idênticas de constante de mola k = 7850N/m estão
ligadas a um bloco de massa 0.245kg.
Qual é a frequência de oscilação
sobre a superfície sem atrito?[Halliday and Resnick, 1997]
27. A Figura 11 mostra um bloco de massa 0.200kg deslizando para a direita
sobre uma superfície elevada sem atrito com uma velocidade de 8.00m/s.
6
Figure 10: Diagrama esquemático referente a questão 26.
Figure 11: Diagrama esquemático do exercício 27
Esse bloco atravessa uma colisão elástica um bloco estacionário 2 está
ligado a uma mola de constante
k = 1208.5N/m.
(Assuma que a mola não
é afetada pela colisão). Depois da colisão o bloco 2 oscila num movimento
harmônico simples com período de 0.140s, e bloco 1 desliza de volta para
a extremidade oposta da superfície elevada aterrizando a uma distância
da base da superfície depois de cair de uma altura
valor de
d?
h = 4.90m.
d
Qual é o
[Halliday and Resnick, 1997]
28. Na Figura 12, um bloco pesando 14N, que pode deslizar sem fricção sobre
uma superfície inclinada de um ângulo
θ = 40◦ , está conectado ao topo do
plano inclinado por uma mola sem massa de comprimento natural 0.450m
e constante de mola 120N/m. (a) Qual distante do topo do plano inclinado
está na posição de equilíbrio? (b) se o bloco for deslocado suavemente para
baixo no plano inclinado então liberado Qual será o período resultante das
oscilações? [Halliday and Resnick, 1997]
29. Um relógio de cuco, cujo cuco tem massa 200g, vibra horizontalmente
sem atrito no extremo de uma mola horizontal, com
k = 7, 0N/m.
O cuco
fechado no relógio está a 5,0cm da sua posição de equilíbrio. Determine:
Figure 12: Diagrama esquemático do problema 28
7
(a) A sua velocidade máxima.
(b) A sua velocidade quando está a 3,0 cm da sua posição de equilíbrio.
(c) Qual é o valor da aceleração em cada um dos casos anteriores?[Beneti,
2015]
30. Um corpo oscila com um MHS ao longo do eixo dos x. O seu deslocamento
varia com o tempo de acordo com a equação:
x = (4.0m) cos (ωt + φ) .
(a) Determine a amplitude, frequência e período do movimento.
(b) Calcule o deslocamento, a velocidade e a aceleração do corpo para
t=1,0s.
(c) Calcule o deslocamento do corpo entre t=0 e t=1,0s.[Beneti, 2015]
31. Numa certa praia e num determinado dia do ano, a maré faz com que a
superfície do mar suba e desça uma distância
d num movimento harmônico
simples, com um período de 12,5 horas. Quanto tempo leva para que a
d
d
4 da sua altura máxima? (Dica: 4 da oscilação
completa é metade da amplitude).[Beneti, 2015]
água desça uma distância
32. Em um barbeador elétrico, a lâmina se move para frente e para trás, ao
longo de uma distância de 2mm, em um MHS com uma frequência de
120Hz.
Determine (a) a amplitude, (b) a velodiade máxima da lâmina
e (c) o módulo da aceleração máxima da lâmina.[Halliday and Resnick,
1997]
33. Quando um bloco de massa
stante de mola
k
m
é conectado a uma mola suspensa de con-
na extremidade livre, ele se desloca num movimento
harmônico simples com período de 5 segundos. O experimento é repetido
com um bloco de massa
M
e verica se que o período passa a ser de 10
segundos. Qual a relação entre as massas
m
e
M?
34. A Figura 13 ilustra o potencial unidimensional de uma barreira de energia
U (x) tem a forma bx2 , e a escala
Uy = 2.0J). (a) Se a partícula passa
para uma partícula de 2kg (a função
do eixo vertical é determinada por
pela posição de equilíbrio com uma velocidade de 85cm/s, ela irá retornar
antes de atingir
x = 15cm?
(b) Se sim, em que posição ela fará isso; e se
não qual a velocidade da partícula em x igual a 15cm?
35. A Figura mostra a energia cinética
em função da posição
x.
K
de um oscilador harmônico simples
Escala vertical é determinada por
Ky = 4.0J.
Qual é a constante da mola?
36. Considere que a energia de um sistema massa mola seja
Se a sua energia potencial for de
3
K = 10
Em = 15 × 103 J.
J, qual a posição em que ele se
encontra em relação a posição de equilíbrio. Qual a sua energia cinética?
Qual a velocidade correspondente, se a massa for
8
m = 5kg?
Figure 13: Gráco relativo ao exercício 34.
Figure 14: Gráco
K = K (x)
relativo ao exercício 35.
37. Considere um sistema massa mola constituído por duas molas em paralelo,
conforme ilustrado na Figura 15 . Qual a energia mecânica desse sistema
se a massa for puxada de 5cm?
38. Determine qual a posição na qual a energia mecânica de um sistema massa
mola de constante
k
e amplitude
xm
é igualmente dividida entre a energia
cinética e a energia potencial.
39. Considere que o dispositivo propulsor de uma arma de fogo seja capaz de
disparar um projétil de 10g a uma velocidade de 435m/s. Se esse sistema
fosse substituido de um sistema massa-mola, qual deveria ser a constante
da mola capaz de produzir o mesmo disparo caso ela seja comprimida de
apenas um centímetro?
40. Digamos que você disponha de um conjunto de molas todas de mesma
constante
k,
e elas sejam usadas em um sistema massa mola suspenso.
Quantas molas devem ser associadas em paralelo para produzir uma frequência 64 vezes maior que a frequência de uma mola só acoplada a massa?
K
versus a posição de três
osciladores harmônicos que tem a mesma massa.
Ordene os grácos de
41. A Figura 16 mostra grácos da energia cinética
acordo com (a) a constante da mola e (b) o período do oscilador, do maior
para o menor.
Halliday and Resnick [1997]
9
Figure 15: Diagrama esquemático relativo ao exercício 37.
duas molas tem a mesma constante
k = 10N/cm,
Considere que as
e que a massa do bloco seja
de 10kg.
Figure 16: Grácos de energia referente ao exercício 41.
10
Figure 17: Gráco de
v (t)
do exercício 42.
42. Qual é a constante de fase de um oscilador harmônico com função velocidade
v (t)
descrita pelo gráco da Figura 17 se a posição é dada pela
expressão
x = xm cos (ωt + φ) .
A escala do eixo vertical é dado por
vs =4.0cm/s.
Halliday and Resnick
[1997]
43. Um oscilador harmônico simples consiste de uma massa de 2.0kg acoplado
Quando t = 1.00s, a posição e a
x =0.129m e v =3.415m/s. (a) Qual é a amplitude
(b) Quais eram a posição e a velocidade em t = 0s?Halliday
a uma mola de constante 100N/m.
velocidade do bloco são
das oscilações?
and Resnick [1997]
π
6 , e a posição
φ), qual a razão entre a energia
44. Se a constante de fase de um sistema massa-mola em MHS é
do bloco é dada por
x = xm cos (ωt +
t = 0?Halliday
cinética e potencial no instante
and Resnick [1997]
45. Calcule a energia necessária para comprimir uma mola de constante de
fase
k = 1000N/m
de 2cm.
46. Determine a velocidade de uma massa de 2kg acoplada a uma mola no
instante
t = 5s,
sabendo que esse sistema foi comprimido de 5cm e passou
a oscilar com uma frequência de 200Hz.
47. Prove que se a massa de um sistema for reduzida a metade, sua frequência
√
será ampliada de um fator igual a
2.
References
Alysson Beneti.
2015. URL
Problemas de Oscilacoes e Movimento Harmonico Simples,
http://fisicasemmisterios.webnode.com.br.
David Halliday and Robert Resnick. Fundamentos de física. In
de Física. Compañía Editorial Continental, 1997.
Paul A Tipler and Gene Mosca.
Fundamentos
Física para cientistas e engenheiros. Macmillan,
1995.
11