(1) (50,0 pontos) As quatro esferas de 2,5 kg - LACTEA

Gabarito P2
TEA008 - Mecânica dos Sólidos II - Engenharia Ambiental - UFPR
Data: 17/10/2016
Professor: Emílio G. F. Mercuri
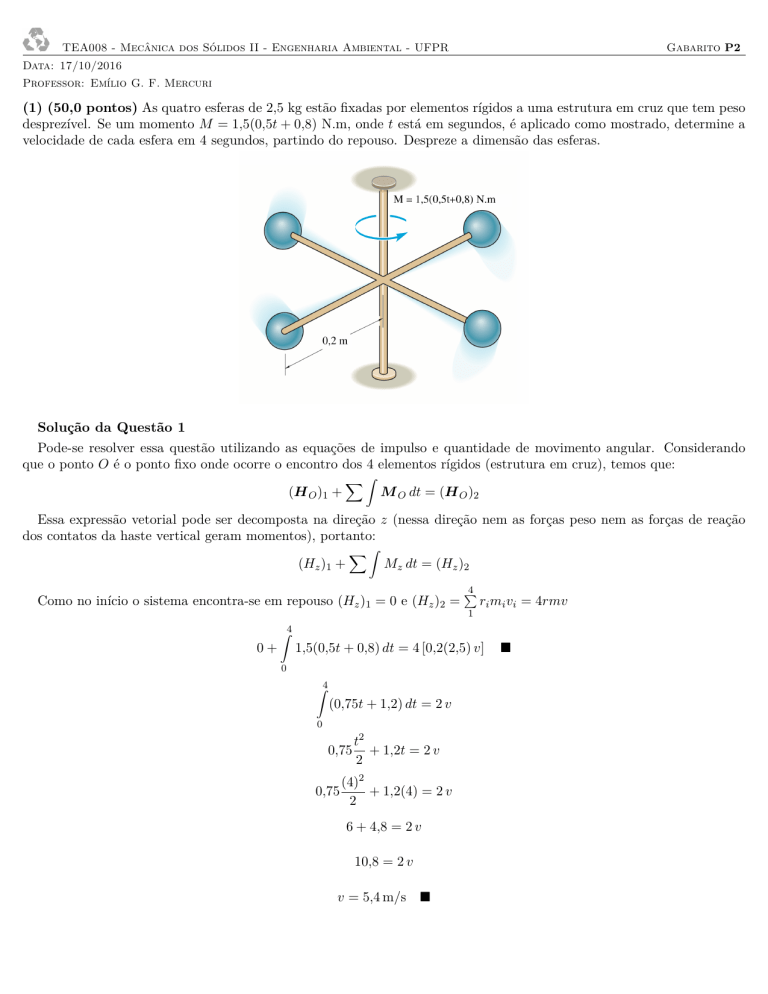
(1) (50,0 pontos) As quatro esferas de 2,5 kg estão fixadas por elementos rígidos a uma estrutura em cruz que tem peso
desprezível. Se um momento M = 1,5(0,5t + 0,8) N.m, onde t está em segundos, é aplicado como mostrado, determine a
velocidade de cada esfera em 4 segundos, partindo do repouso. Despreze a dimensão das esferas.
Solução da Questão 1
Pode-se resolver essa questão utilizando as equações de impulso e quantidade de movimento angular. Considerando
que o ponto O é o ponto fixo onde ocorre o encontro dos 4 elementos rígidos (estrutura em cruz), temos que:
(H O )1 +
XZ
M O dt = (H O )2
Essa expressão vetorial pode ser decomposta na direção z (nessa direção nem as forças peso nem as forças de reação
dos contatos da haste vertical geram momentos), portanto:
(Hz )1 +
XZ
Mz dt = (Hz )2
Como no início o sistema encontra-se em repouso (Hz )1 = 0 e (Hz )2 =
4
P
ri mi vi = 4rmv
1
Z4
1,5(0,5t + 0,8) dt = 4 [0,2(2,5) v]
0+
0
Z4
(0,75t + 1,2) dt = 2 v
0
0,75
0,75
t2
+ 1,2t = 2 v
2
(4)2
+ 1,2(4) = 2 v
2
6 + 4,8 = 2 v
10,8 = 2 v
v = 5,4 m/s
(2) (50.0 pontos) O anel C se move ao longo da haste BA com velocidade de 3 m/s e aceleração de 0,5 m/s2 , ambas
direcionadas de B para A e medidas em relação à haste. Concomitantemente, a haste BA rotaciona com velocidade e
aceleração angulares mostradas. Determine a velocidade e aceleração do anel nesse instante.
Solução da Questão 2
Esse problema pode ser resolvido utilizando dois eixos de referência. Um sistema de referência x,y,z que rotaciona junto
com a haste AB e outro sistema de referência X,Y,Z que é fixo e coincide com o sistema móvel no instante mostrado.
Usaremos as seguintes equações para resolver o problema:
v C = v B + ω × r + v rel
aC = aB + ω̇ × r + ω × (ω × r) + 2ω × v rel + arel
sendo que ω representa a velocidade angular dos eixos que giram e ω̇ representa a aceleração angular dos eixos que giram.
Portanto, sabemos que:
v B = aB = 0
ω = 6k rad/s
α = ω̇ = 1,5k rad/s2
Sobre o movimento relativo do anel C com relação ao sistema x,y,z, nós temos:
r = 0,5j m
v rel = 3j m/s
arel = 0,5j m/s2
Aplicando a equação da velocidade:
v C = v B + ω × r + v rel
v C = 0 + 6k × 0,5j + 3j
v C = −3i + 3j m/s Aplicando a equação da aceleração:
aC = aB + ω̇ × r + ω × (ω × r) + 2ω × v rel + arel
aC = 0 + 1,5k × 0,5j + 6k × (6k × 0,5j) + (2)6k × 3j + 0,5j
aC = −36,75i − 17,5j m/s2 Relações Matemáticas
ΣM G P
= Ḣ G
H 0 = r i × mi v i
H P = H G + ρ × mv
ΣMP = Iα + mad
v A = v B + ω × r + v rel
ΣF = mā
∆G = I 1−2
T = 12 mv 2
T1 + U1−2 = T2
ΣF = Ġ
∆H = Impulso angular1−2
Ve = 21 kx2
0
T1 + V1 + U1−2
= T2 + V2
aA = aB + ω̇ × r + ω × (ω × r) + 2ω × v rel + arel
ΣM 0 = Ḣ 0
G = mv
Vg = mgh
ΣM0 = I0 α