Eletromagnetismo e Ótica (MEAer/LEAN)
Lei de Gauss
3ª Semana
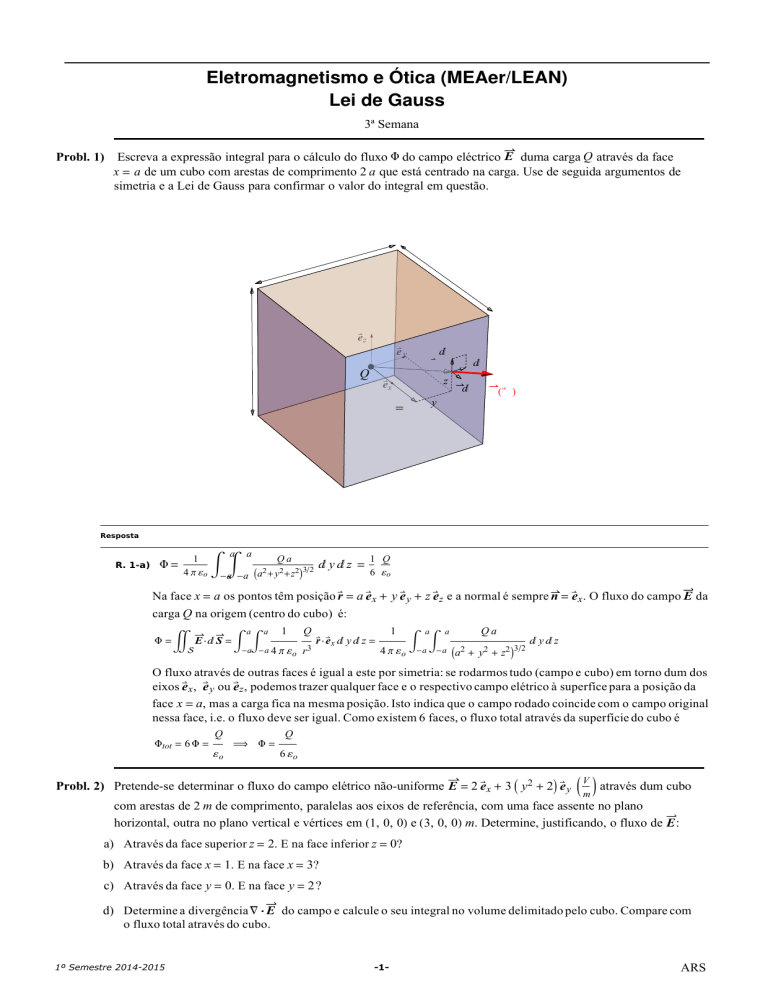
Probl. 1) Escreva a expressão integral para o cálculo do fluxo Φ do campo eléctrico E duma carga Q através da face
x = a de um cubo com arestas de comprimento 2 a que está centrado na carga. Use de seguida argumentos de
simetria e a Lei de Gauss para confirmar o valor do integral em questão.
2a
2a
ez
ey
2a
Q
ⅆz
rs
z
ex
x a
y
ⅆy
nⅆS
E (r s )
Resposta
R. 1-a)
Φ=
1
4 π εo
a
a
Qa
2
2 2
-a -a a +y +z
3/2
ⅆ yⅆz =
1 Q
6 εo
Na face x = a os pontos têm posição r = a ex + y e y + z ez e a normal é sempre n = ex . O fluxo do campo E da
carga Q na origem (centro do cubo) é:
a
Φ = E · ⅆ S =
-a
Q
1
Qa
a
a
r · ex ⅆ y ⅆ z =
ⅆ yⅆz
-a 4 π εo r3
4 π εo -a -a a2 + y2 + z2 3/2
a
1
O fluxo através de outras faces é igual a este por simetria: se rodarmos tudo (campo e cubo) em torno dum dos
eixos ex , e y ou ez , podemos trazer qualquer face e o respectivo campo elétrico à superfíce para a posição da
face x = a, mas a carga fica na mesma posição. Isto indica que o campo rodado coincide com o campo original
nessa face, i.e. o fluxo deve ser igual. Como existem 6 faces, o fluxo total através da superfície do cubo é
Φtot = 6 Φ =
Q
Q
⟹ Φ=
εo
6 εo
V
Probl. 2) Pretende-se determinar o fluxo do campo elétrico não-uniforme E = 2 ex + 3 y2 + 2 e y através dum cubo
m
com arestas de 2 m de comprimento, paralelas aos eixos de referência, com uma face assente no plano
horizontal, outra no plano vertical e vértices em (1, 0, 0) e (3, 0, 0) m. Determine, justificando, o fluxo de E:
a) Através da face superior z = 2. E na face inferior z = 0?
b) Através da face x = 1. E na face x = 3?
c) Através da face y = 0. E na face y = 2?
d) Determine a divergência ∇ · E do campo e calcule o seu integral no volume delimitado pelo cubo. Compare com
o fluxo total através do cubo.
1º Semestre 2014-2015
-1-
ARS
Resposta
R. 2-a)
Φz=0 = 0 = Φz=2
n = ± ez ⟹ E · n ⅆ S = 0
R. 2-b)
Φx=1 = -8 = -Φx=3
Nm2
C
n = ± ex ⟹ E · n ⅆ S = ± 2 ⅆ y ⅆ z
R. 2-c)
Φ y=0 = -24
Nm2
C
Nm2
; Φ y=2 = 72
C
n = ± e y ⟹ E · n ⅆ S = ± 3 y2 + 2 ⅆ x ⅆ z
R. 2-d)
∇ · E = 6 y ;
∇ · E ⅆ V = 48
cubo
Probl. 3) Um eletrão é disparado na direcção perpendicular a uma superfície plástica uniformemente carregada. A
m
superfície é plana e de área muito grande. A velocidade inicial do eletrão é v o = 2 × 105 e ao fim de 7 picos
segundos o eletrão pára e volta para trás. Qual é a densidade superficial de carga σ no plástico?
Resposta
R. 3-a)
σ = 2.87 ×10-6
C
m2
O electrão é uniformemente desacelerado no campo E =
σ
2 εo
sgn(z) ez do plano de cargas de densidade σ. A
força que actua sobre o eletrão é F = qe E. A aceleração do eletrão é az =
Δv
Δt
=-
vo
,
Δt
onde Δt = 7 × 10-12 s.
Assim
me a = F ⟺ -me
vo
Δt
= qe
onde me = 9.109383 ×10
σ
2 εo
-31
⟹ σ =-
me 2 εo vo
qe
Δt
kg e qe = 1.6021766 ×10-19 C .
Probl. 4) Dois planos verticais paralelos, práticamente infinitos, estão separados por uma distância 2 d na direção ex . Um
C
dos planos está uniformemente carregado com uma densidade de carga σ1 m2 , enquanto o outro possui uma
densidade de carga σ2 = 2 σ1 .
a) Use a Lei de Gauss para determinar o campo elétrico E em todas as regiões do espaço.
b) Determine a descontinuidade do campo elétrico E ao atravessar cada plano.
c) Determine a força (magnitude, direção e sentido) por unidade de área sentida por cada plano.
d) Determine o potencial elétrico ϕ em todas as regiões do espaço, assumindo que ϕ = 0 num ponto a igual distância
dos planos.
e) Qual é a energia cinética que um electrão ganharia se fosse largado do repouso de uma das armaduras e acelerado
pelo campo até atingir a outra? Há diferença na posição inicial do eletrão se os planos estiverem positiva ou
negativamente carregados?
ey
σ1
2 σ1
2d
ex
O
ARS
-2-
1º Semestre 2014-2015
Resposta
3 σ1
ex
2 εo
σ
- 1 ex
2 εo
3σ
+ 1 ex
2 εo
-
R. 4-a)
E(r) =
(x < -d)
(-d < x < d)
(d < x)
O campo em cada região é a soma dos campos de cada plano separadamente nessa região. O campo do plano
σ
da esquerda é E1 (x) = 1 sgn(x + d) e x , i.e. troca de sinal quando x = -d , enquanto o campo do plano da
2 εo
sgn(x - d) e x e troca de sinal quando x = d .
Quando x < -d ambos os campos são dirigidos no sentido -ex e a sua soma é
σ1 +σ2
E(x) = E1 (x) + E2 (x) = ex.
σ2
2 εo
direita é E2 (x) =
2 εo
σ +σ
Quando x > d temos ambos os campos na direcção ex , pelo que E(x) = 1 2 ex .
2 εo
Numa posição entre os planos, -d < x < d , o campo total é E(x) = E1 (x) + E2 (x) =
σ1 -σ2
2 εo
ex.
σ1
εo
2 σ1
εo
ΔE x (-d) =
R. 4-b)
ΔE x (d) =
Através de uma superfície carregada com densidade de carga σ a componente do campo elétrico normal à
σ
superfície sofre uma descontinuidade Δ E ·n = .
εo
R. 4-c)
Δ F1
ΔS
=-
Δ F2
ΔS
=
σ1 2
εo
σ1 2
εo
ex
ex
A carga ⅆ q = σ ⅆ S de um elemento de área ⅆ S de cada plano está sujeita à força devida ao campo do outro
plano. (As cargas do próprio plano não exercem uma força sobre ⅆ q. Porquê?) Assim:
ⅆ F 1 (-d) = ⅆ q1 E2 (-d) = -σ1
R. 4-d)
σ1 (2 d+3 x)
2 εo
σ1 x
2 εo
σ1 (4 d-3 x)
2 εo
ϕ (x) =
σ2
2 εo
ⅆ S ex
;
ⅆ F 2 (d) = ⅆ q2 E1 (d) = σ2
(x > d)
σ1 <0
d
-d
φ(x) (V)
φ(x) (V)
ⅆ S ex
(-d < x < d)
d
0
2 εo
(x < -d)
σ1 >0
-d
σ1
0
0
0
x→
x→
O potencial associado a um campo elétrico conhecido E é determinado em relação a um ponto de referência ro
através da definição
x
ϕ (r) = ϕ (ro ) - E · ⅆ r ⟹ ϕ (x) = ϕ (xo ) - E x (s) ⅆ s
ro ,r
xo
Como o campo só tem componente E x , as superfícies equipotenciais são planos perpendiculares a ex , ou seja
paralelos aos planos de carga donde ϕ(r) ≡ ϕ(x).
1º Semestre 2014-2015
-3-
ARS
Como o campo muda de forma em x = ±d podemos começar por calcular ϕ(x) em x ∈ [-d, d] sabendo que
ϕ(0) = 0
x
ϕ (x) = ϕ (0) -
0
-
σ1
ⅆs =
2 εo
Isto significa que ϕ(-d) = x
ϕ (x) = ϕ (-d) -
-d
3 σ1
2 εo
σ1 x
(x ∈ [-d, d])
2 εo
σ1 d
2 εo
ⅆs = -
pelo que para x < -d podemos usar ro = -d ex para calcular
σ1 d
+
2 εo
3 σ1
2 εo
(x + d)
De forma idêntica se calcula ϕ(x) para x > d sabendo que ϕ(d) =
R. 4-e)
ΔK = -qe
σ1 d
2 εo
σ1 d
εo
Porque o campo elétrico é conservativo, a energia total do eletrão deve ser constante, ou seja a variação da
energia potencial ΔU é igual em magnitude e de sinal contrário à variação da energia cinética ΔK . A
diferença de potencial entre as armaduras é Δϕ = ϕ(d) - ϕ(-d) =
σ1 d
,
εo
pelo que a variação de energia
potencial do eletrão é ΔU = qe Δϕ = -ΔK . Se as armaduras estiverem positivamente carregadas a posição
inicial do eletrão deve ser junto da armadura menos carregada. A situação inverte-se se as armaduras
estiverem negativamente carregadas, ou seja o eletrão deve sair junto à armadura mais carregada.
Probl. 5) Um cilindro não-condutor, muito fino e comprido, tem 2 nC de carga uniformemente distribuída por cada metro
de comprimento. O cilindro é coaxial com um tubo condutor ôco, descarregado, de raio interior a = 5 cm e
exterior b = 10 cm.
a) Qual é a magnitude e direcção do campo elétrico à distância d = 15 cm do eixo comum dos cilindros?
b) Qual é a densidade superficial de carga na superfície interna do cilindro condutor? E na superfície externa?
c) Qual é a carga por metro na superfície interior e exterior do cilindro condutor?
Resposta
R. 5-a)
V
E (d) = 240 er (θ) em coordenadas cilíndricas com ez coincidente com o eixo dos cilindros.
m
O fluxo através de um cilindro de Gauss, de altura h e raio d = 15 cm, coaxial com os outros cilindros, é
apenas devido à superfície lateral S , uma vez que nas bases E ·n = 0. Pela simetria cilíndrica da distribuição
de cargas, o campo deve ser E (r) = Er (r) er (θ) em coordenadas cilíndricas r, θ, z, com eixo ez coincidente
com o cilindro não-condutor. A carga interior ao cilindro de Gauss é λ h porque o cilindro condutor ôco está
descarregado.
Φd = E · ⅆ S = Er (d) 2 π d h =
λh
S
R. 5-b)
σ (a) = -
20
π
nC
m2
; σ (b) =
10
π
⟹
εo
Er (d) =
λ
2 π εo d
nC
m2
Se repetirmos o cálculo anterior com um cilindro de Gauss com raio r ∈ [a, b], i.e. com a superfície lateral
dentro do cilindro condutor, devemos concluir que o fluxo total é zero uma vez que dentro dos condutores em
equilíbrio eletrostático não há campo elétrico, E (r) = 0. Mas então a carga interior à superfície de Gauss deve
somar zero, e como λ h é a contribuição do cilindro não-condutor, a contribuição das cargas na superfície
interior do condutor deve ser -λ h para que o total se anule. Então a densidade superficial interior deve ser
λh
σ (a) = R. 5-c)
2πah
λh
λ
=-
2πa
λ (a) = -λ (b) = -2
⟹ σ (b) =
2πbh
λ
=
2πb
nC
m
Probl. 6) Um tubo cilíndrico ôco muito comprido é constituído por um material não-condutor, tem um raio interior R1 e
C
espessura constante a, e está uniformemente carregado com uma densidade de carga ρ m3 . Use a Lei de Gauss
para determinar:
a) O campo elétrico E o (r) dentro da cavidade do tubo, ou seja, para distâncias ao eixo r < R1 .
b) O campo elétrico E 1 (r) entre as faces interior e exterior do tubo, assumindo que a permitividade elétrica aí é
também εo .
ARS
-4-
1º Semestre 2014-2015
c) O campo elétrico E 2 (r) na vizinhança exterior do tubo não muito perto das extremidades.
d) Determine o potencial elétrico ϕ(r) nas regiões mencionadas acima assumindo que ϕ=0 num ponto do eixo do
tubo.
Resposta
R. 6-a)
Eo (r) = 0
Devido à simetria cilíndrica E (r) = Er (r) er (θ). Para distâncias r < R1 o fluxo através de um cilindro de
Gauss de raio r e altura h, coaxial com o tubo, é
Φ (r) = E · ⅆ S = Er (r) 2 π r h = 0 ⟹ Er (r) = 0
porque não existem cargas na parte ôca do tubo.
R. 6-b)
ρ r2 -R1 2
N
V
E1 (r) =
er (θ) ≡
C
2 εo r
m
Para distâncias r ∈ [R1 , R1 + a], o fluxo através de um cilindro de Gauss de raio r e altura h, coaxial com o
tubo, é proporcional à carga interior ao cilindro de Gauss, ou seja a densidade de carga ρ × volume do cilindro
entre R1 e r.
Φ (r) = E · ⅆ S = Er (r) 2 π r h =
ρ π r2 - R21 h
εo
R. 6-c)
⟹ Er (r) =
ρ r2 - R1 2
2 εo r
ρ a (a+2 R1 )
N
V
E2 (r) =
er (θ) ≡
C
m
2 εo r
Fora do tubo, para r > R1 + a, a carga interior ao cilindro de Gauss de raio r e altura h é a carga na secção do
tubo com altura h, ou seja
Φ (r) = E · ⅆ S = Er (r) 2 π r h =
ρ π (R1 + a)2 - R21 h
εo
0
R. 6-d)
ϕ (r) =
ρ a (a + 2 R1 )
⟹ Er (r) =
2 εo r
(0 ≤ r ≤ R1 )
ρ R 21
1 + 2 log
4 εo
ϕ (R1 + a) -
r
R1
-
r
R1
2
(R1 ≤ r ≤ R1 + a)
ρ a (a+2 R1 )
r
log
R1 +a
2 εo
(R1 + a ≤ r)
Para pontos em que r ∈ [0, R1 ] o campo elétrico nulo implica que o potencial é constante, igual ao valor de
ϕ (0) = 0. Entre r = R1 e r = R1 + a, ou seja, dentro do tubo, o potencial pode ser calculado a partir do campo
elétrico tendo em conta que ϕ (R1 ) = 0.
ϕ (r) = ϕ (R1 ) -
R1 ,r
E · ⅆ r = -
r
R1
Er (s) ⅆ s
Para r > R1 , obtemos, usando ϕ (R1 + a) =
ϕ (r) = ϕ (R1 + a) -
R1 +a,r
⟹
ϕ (r) =
ρ R 21
4 εo
E · ⅆ r = ϕ (R1 + a) -
r
R1 +a
ρ R21
2 εo
r
1
R1
s
s
-
1 + 2 log R1 +a -
R1
ρ a (a + 2 R1 )
2 εo s
R21
ⅆs
R1 +a 2
R1
acabado de calcular,
ⅆs
Probl. 7) Uma esfera ôca, feita de um material não-condutor, tem raio interior a e exterior b, e uma carga total Q
uniformemente distribuida pelo material. Determine o campo elétrico E nas seguintes regiões:
a) Fora da esfera.
b) Dentro do material da esfera.
c) Na parte ôca no interior da esfera.
Resposta
R. 7-a)
E=
Q
1
4 π εo r 3
r quando r > b.
Usando uma superfície de Gauss esférica r , de raio r > b, concêntrica com a esfera ôca, obtemos da simetria
esférica da distribuição de carga que o campo deve ser radial, E = Er (r) er (θ, φ) em coordenadas esféricas. O
fluxo através da superfície de Gauss r é assim, uma vez que Er (r) é aí constante,
1º Semestre 2014-2015
-5-
ARS
Φ (r) =
r
E · ⅆ S = Er (r)
r
ⅆ S = Er (r) 4 π r2 =
Q
εo
⟹ Er (r) =
1
Q
4 π εo r 2
Isto é idêntico ao campo, a distâncias r > b, de uma carga pontual de magnitude Q, posicionada no centro da
esfera ôca. Para distâncias r < b o campo é diferente do da carga pontual.
R. 7-b)
E=
Q
1
4 π εo r 3
r3 -a3
r
b3 -a3
quando a ≤ r ≤ b.
Como a esfera é não-condutora, a carga total Q está uniformemente distribuída pelo volume da esfera ôca com
densidade ρ =
Q
4
3
π b3 -a3
. Para distâncias r ∈ [a, b] uma esfera de Gauss de raio r apenas conterá uma fracção
da carga total da esfera ôca, ou seja
Qint (r) = ρ
R. 7-c)
4
3
r 3 - a3
π r3 - a3 = Q
b3 - a 3
⟹ Φ (r) = Er (r) 4 π r2 =
Q r 3 - a3
εo b3 - a 3
E = 0 quando r < a.
Dentro da esfera ôca não existem cargas, logo o fluxo através de uma superfície de Gauss de raio r ∈ [0, a]
deve ser nulo. Se existisse campo elétrico teria a mesma simetria esférica que no exterior, donde
Φ (r) = Er (r) 4 π r2 = 0 ⟹ Er (r) = 0
Probl. 8) Uma esfera não-condutora de raio R tem uma carga distribuída em volume com uma densidade ρ = α r
Determine:
C
.
m3
a) A carga total Q da esfera.
b) O campo elétrico E num ponto arbitrário fora da esfera.
c) O campo elétrico E num ponto arbitrário dentro da esfera.
d) As expressões do potencial elétrico dentro e fora da esfera, assumindo ϕ∞ = 0.
Resposta
R. 8-a)
Q = α π R4
Para uma densidade ρ (r) = α r a carga total será, usando coordenadas esféricas com ⅆ V = r2 sin(θ) ⅆ r ⅆ θ ⅆ φ,
2π π R
Q =
R. 8-b)
E=
esf .
ρ (r) ⅆ V =
0
1 α R4
4 εo r 2
α r3 sin(θ) ⅆ r ⅆ θ ⅆ φ
0 0
er
Usando a lei de Gauss para uma esfera de raio r > R obtém-se
Er (r) =
R. 8-c)
E=
Q
1
4 π εo r 2
1
4 εo
α r2 er
Para uma superfície de Gauss esférica de raio r < R, a sua carga interior é
r
Qint (r) =
s<r
ρ (s) ⅆ V = 4 π α s3 ⅆ s = α π r4
0
pelo que o fluxo do campo elétrico através dessa superfície de Gauss é
Φ (r) = Er (r) 4 π r2 =
R. 8-d)
α π r4
εo
⟹ Er (r) =
1 α R4
4 εo r
1
α 4 R3 - r3
12 εo
ϕ (r) =
1
4 εo
α r2
r>R
r<R
Do lado de fora da esfera o potencial comporta-se como o de uma carga pontual Q = α π R4 na origem, pelo
que
1
ϕ (r) =
Q
4 π εo r
(r > R)
Dentro da esfera o potencial pode ser calculado a partir do campo E e do potencial à superfície da esfera
ARS
-6-
1º Semestre 2014-2015
potencial pode
1
4 εo
ϕ (R) =
partir
campo
potencial superfície
α R3 .
1
r
ϕ (r) = ϕ (R) -
R
4 εo
1
α s2 ⅆ s =
α R3 -
4 εo
1
12 εo
α r3 - R3
Probl. 9) Duas esferas condutoras, ôcas e concêntricas, de raios R1 = 2 cm e R2 = 6 cm e espessura desprezável são
carregadas até atingirem potenciais ϕ1 = 6 V e ϕ2 = 1 V .
a) Deduza a expressão para o potencial ϕ (r) em todas as regiões do espaço.
b) Determine o campo eléctrico E nas mesmas regiões. Devem-se esperar descontinuidades no campo elétrico? Onde
e porquê ?
c) Calcule as cargas Q1 e Q2 de cada esfera.
d) Determine a capacidade C deste sistema visto como um condensador.
e) Qual é a pressão electroestática à superfície da esfera interior?
Respostas:
6
R. 9-a)
(r ≤ R1 )
3
20
3
ϕ(r) =
1
r
- 10 (R1 ≤ r ≤ R2 ) (V )
(R2 ≤ r)
50 r
O potencial de cada esfera condutora é da forma (assumindo ϕ∞ = 0 e a1 =
ϕ1 (r) =
ϕ2 (r) =
a1
r
a2
r
(r > R1 ) ;
(r > R2 )
ϕ1 (r) =
;
ϕ2 (r) =
a1
q1
q
,a = 2 )
4 πεo 2
4 πεo
(r ≤ R1 )
R1
a2
(r ≤ R2 )
R2
Assim, nas várias regiões podemos somar o potencial das duas esferas, obtendo
ϕ (r) = ϕ1 (r) + ϕ2 (r)
com as condições fronteira
ϕ (R1 ) =
a1
R1
+
a2
R2
= 6V
Destas obtém-se a1 =
6
ϕ (r) =
a1
a
+ 2
r
R2
a1 +a2
r
0
R. 9-b)
E (r ) =
3
20 r 2
3
50 r 2
;
a1
ϕ (R2 ) =
5 R 1 R2
R2 -R1
e a2 =
R2
a2
+
R2
= 1V
(R2 -6 R1 ) R2
R2 -R1
pelo que
(r < R1 )
(R1 ≤ r ≤ R2 )
(r > R2 )
(r ≤ R1 )
er (R1 ≤ r ≤ R2 ) V ;
m
er (R2 ≤ r)
V
V
ΔE r (R1 ) = 375 m e ΔE r (R2 ) = -25 m
O campo elétrico obtém-se do potencial a partir da definição E = -∇ϕ = -
∂ϕ (r)
er .
∂r
Há descontinuidade do campo elétrico sempre que atravessa uma superfície carregada. A descontinuidade da
σ
componente normal do campo é Δ E ·n = .
εo
ΔEr (R1 ) = Er R+
1 - Er (R1 ) =
R. 9-c)
Q1 = 16.6667 (pC)
3
20 R21
;
ΔEr (R2 ) = Er R+
2 - Er (R2 ) =
3
50 R22
3
-
20 R22
e Q2 = -10 (pC)
Uma vez conhecidos a1 =
3
20
e a2 = -
9
100
obtém-se q1 = 4 π εo a1 = 16.6667 pC e q2 = 4 π εo a2 = -10 pC .
Doutra forma, a partir das descontinuidades do campo pode-se obter a densidade superficial de carga em cada
esfera, e a partir daí calcular a respectiva carga total.
1º Semestre 2014-2015
-7-
ARS
R. 9-d)
C = 3.33 (pF)
A capacidade dum condensador é a razão C =
Q
,
V
onde Q representa a carga na armadura positiva e
V = ϕ+ - ϕ- é a tensão entre as armaduras positiva e negativa. Neste caso Q = Q1 = 16.6667 pC e V = 5 V ,
donde C = 3.33 em pico-Farads.
R. 9-e)
p1 = 6.217 ×10-7 Pa
A pressão eletrostática é a força por unidade de área sobre as cargas da armadura interna devido às forças entre
σ2
as cargas nessa armadura. Essa pressão é p1 = 1 = 6.21701 ×10-7 Pa.
2 εo
ARS
-8-
1º Semestre 2014-2015