Guião do trabalho P6 Resistências e Circuitos Eléctricos

Física Laboratorial I
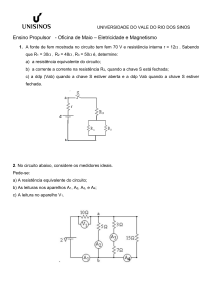
Ano Lectivo 2008/09
TRABALHO PRÁTICO Nº 6 - QUÍMICA E QUÍMICA INDUSTRIAL
RESISTÊNCIA E CIRCUITOS ELÉCTRICOS
Objectivo - Neste trabalho pretende-se clarificar o conceito de resistência eléctrica e verificar leis
aplicáveis a circuitos eléctricos. Considera-se apenas o funcionamento em corrente
contínua, regime em que as grandezas características não são variáveis no tempo.
1. Introdução
1.1. Lei de Ohm e resistência
Para alguns componentes de circuitos, constituídos por materiais condutores, verifica-se uma
relação linear entre a d.d.p. aplicada entre dois pontos A e B do condutor - VAB - e a intensidade da
corrente que os percorre - I . É conhecida como lei de Ohm1 e representa-se
pela expressão:
I
V AB = RI
(1)
A
onde R designa a resistência do material entre os pontos A eB (figura 1). No
Sistema Internacional as grandezas eléctricas referidas têm as seguintes
unidades e símbolos representativos:
V - Volt (V); I - Ampère (A); R - Ohm (Ω).
R
VAB
B
Figura 1
O valor da resistência de um condutor depende da natureza do material que o constitui, do
comprimento do (fio) condutor e da sua secção. Pode, assim, escrever-se:
l
(2)
S
onde ρ é a resistividade eléctrica do condutor, ℓ é o seu comprimento e S é a secção recta. A
resistividade é uma propriedade eléctrica do material que varia com a temperatura e, como tal,
também a resistência aumenta (ou diminui) com o acréscimo de temperatura.
R=ρ
A mais importante razão por que um material aquece ao ser atravessado por corrente eléctrica é o
chamado efeito de Joule que traduz a quantidade de energia eléctrica que é convertida em calor.
Tomando em conta a resistência - R - do condutor, esse efeito é quantificado pela lei de Joule:
P = RI 2
(3)
onde P representa a potência da corrente eléctrica no condutor.
1.2. Geradores de corrente contínua - fontes de tensão
Os geradores são dispositivos que mantêm aos seus terminais uma certa diferença de potencial.
Quando são ligados a um circuito que estabeleça um caminho de corrente entre os dois terminais, os
geradores provocam um movimento permanente de cargas. São exemplos de geradores (de corrente
contínua) as pilhas e baterias. Em laboratório são mais usados equipamentos que convertem a
tensão (e corrente) alternada da rede em tensão (e corrente) contínua. Daí a designação mais
vulgarizada de fontes de tensão.
1
Em rigor este enunciado da lei de Ohm apenas é válido para condutores filiformes; no entanto a experiência mostra
que se conseguem resultados de boa precisão quando se aplica a circuitos alimentados a baixa potência.
Departamento de Física da FCTUC
1/7
Física Laboratorial I
Ano Lectivo 2008/09
Verifica-se experimentalmente que a intensidade da corrente que passa num circuito a que um
gerador (fonte de tensão) está ligado depende da resistência do circuito e também das características
do gerador. O efeito é mais acentuado para alguns tipos de geradores. Para o quantificar fala-se num
comportamento ideal ou real de uma fonte de tensão, como já referido no trabalho P4. No primeiro
caso a tensão gerada pela fonte é independente da corrente fornecida ao circuito (figura 2-a) e tem
valor coincidente com o da sua força electromotriz. Em esquema a fonte é representada apenas pelo
respectivo símbolo (figura 3-a).
Numa fonte real o valor da tensão depende da intensidade da corrente fornecida. Se a
dependência variar de modo linear, como acontece em pilhas para baixas correntes (figura 2-b), a
fonte de tensão pode ser modelada como sendo constituída por uma fonte ideal, de força
electromotriz E, em série com uma resistência, designada por resistência interna (fig. 3-b). Uma
fonte de tensão real tem sempre resistência interna, ainda que esta seja, por vezes, muito pequena e
possa ser desprezada. A tensão entre os pólos da fonte apenas é igual à sua força electromotriz
quando a fonte está em circuito aberto.
VAB
VAB
VAB = Ε
Ε
variação aproximadamente
linear
variação não-linear
Fonte de tensão ideal
Fonte de tensão real
I
I
a) fonte ideal de tensão
b) fonte real de tensão
Figura 2. Variação da tensão VAB aos terminais de uma fonte de tensão de força electromotriz E, em
função da corrente eléctrica fornecida I
A
A
I
I
VA B
E
ri
VA B
R
R
E
VAB = E
B
a) fonte ideal de tensão
VAB = E - ri I
B
b) fonte real de tensão
Figura 3 - Circuito eléctrico alimentado por: a) fonte de tensão ideal; b) fonte de tensão real
1.3. Leis de Kirchoff
As leis de Kirchoff facilitam o tratamento matemático de circuitos eléctricos com várias
ramificações e com vários componentes.
Departamento de Física da FCTUC
2/7
Física Laboratorial I
Ano Lectivo 2008/09
A lei dos nodos baseia-se na conservação da carga eléctrica e permite equacionar e determinar as
correntes que percorrem cada porção de um circuito. Designa-se por nodo um ponto do circuito
onde se ligam três ou mais elementos. A lei pode enunciar-se dizendo que "a soma das correntes
que chegam a um nodo é igual à soma das correntes que dele saem". Na sua aplicação há que dar
atenção ao sentido das correntes, o qual deve ser definido (arbitrariamente) antes de somar.
A lei das malhas baseia-se na propriedade de o campo eléctrico ser conservativo e permite
calcular a queda de tensão em cada um dos elementos de um circuito. Designa-se por malha um
caminho fechado num circuito. A lei pode enunciar-se dizendo que "a soma das diferenças de
potencial ao longo de uma malha é igual a zero". Na sua aplicação há que dar atenção ao sinal das
várias d.d.p.s, que é positivo ou negativo conforme o sentido de circulação coincide ou não com o
da corrente (marcada) no elemento.
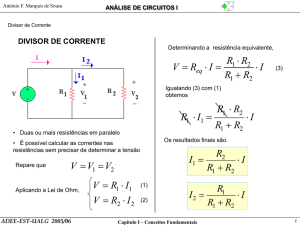
1.4. Associação de resistências
Na análise de circuitos eléctricos encontram-se por vezes resistências que se ligam em sequência
e são, portanto, percorridas pela mesma corrente. Nesse caso diz-se que estão em série e, no
tratamento matemático, é possível substituí-las de modo expedito por uma só resistência cujo valor
n
seja igual à soma de todas: Req = ∑ Ri
(4)
i =1
Outra situação de fácil tratamento é a de resistências que tenham os dois extremos ligados aos
mesmos pontos. Nesse caso a d.d.p. entre extremos é igual para todas; diz-se que estão em paralelo.
É possível substituí-las por uma só resistência cujo inverso de valor seja igual à soma dos inversos
n
1
1
dos valores de todas:
=∑
(5).
Req i =1 Ri
Na prática é preciso não esquecer que uma só resistência deve dissipar o calor libertado em todas!
2. Realização experimental
Para realização das várias experiências vai ser necessário usar uma fonte de tensão contínua
variável, um multímetro funcionando como voltímetro, outro multímetro funcionando como
amperímetro, resistências fornecidas e uma placa de ligações. A placa de ligações é um acessório
que facilita a interligação dos vários elementos. Os diversos "buraquinhos" onde se "enfiam" os
terminais estão, internamente, ligados entre si. Mas não todos, naturalmente! É preciso informar-se
de como são feitas as conexões internas.
2.1. Verificação experimental da lei de Ohm
Comece por montar o circuito indicado na figura 4. Não ligue o gerador, mas rode o controlo de
tensão totalmente para a esquerda. Use a resistência que se encontra na placa, que é igual ou
superior a 330 Ω, ou chame ajuda.
Como a figura bem elucida, os dois multímetros têm função diferente e são ligados, um em série
com a resistência e o outro em paralelo. O primeiro vai medir a corrente e o segundo a tensão. Não
se esqueça de seleccionar em cada um a escala de maior precisão para o valor que está a ler.
2.1.1. Comece por calcular o valor máximo da tensão que pode aplicar na resistência. Para o efeito
precisa de saber o valor da resistência. Identifique-o com base no respectivo código de cores.
A resistência que está a usar pode dissipar o calor devido a uma potência máxima de 1 W.
Com base nas expressões (1) e (3) calcule o valor pretendido. Registe na folha de dados.
Departamento de Física da FCTUC
3/7
Física Laboratorial I
Ano Lectivo 2008/09
A
V
Figura 4. Ligações para verificação experimental da lei de Ohm
2.1.2. Ligue o gerador. Com auxílio do voltímetro, rode o controlo de tensão até atingir um valor
um pouco inferior ao que calculou. Registe esse valor na primeira linha da tabela 1 da folha
de registo de dados. Registe também a leitura do amperímetro.
2.1.3. Diminua a tensão do gerador em intervalos de cerca de 2 V e prossiga as leituras de tensão e
corrente até preencher completamente a tabela 1.
2.2. Determinação da resistência interna de pilhas comerciais
Material necessário: duas pilhas comerciais (uma do tipo zinco-carvão (ou salina) e outra do tipo
alcalino), resistências de valor conhecido (caixa de resistências), um voltímetro
digital e uma placa de ligações.
2.2.1. Utilizando o voltímetro digital, meça a força electromotriz (E) da pilha alcalina, ligando
apenas o voltímetro aos seus terminais (fonte em vazio). Registe esse valor na tabela 2.
A
2.2.2. Monte o circuito representado na figura 5 em que
E e ri representam a pilha (fonte real de tensão) e
R é um valor de resistência a seleccionar dos
vários possíveis de uma caixa de resistências.
2.2.3. Para cada valor de R, seleccionado de acordo
com a tabela 2, meça com o voltímetro a tensão
aos terminais da resistência (VAB). Registe os
valores lidos na respectiva coluna.
2.2.4. Repita os procedimentos anteriores para a outra
pilha de que dispõe.
Departamento de Física da FCTUC
I
ri
R
VAB
E
VAB = E - riI
B
Figura 5
4/7
Física Laboratorial I
Ano Lectivo 2008/09
2.3. Verificação experimental das leis de Kirchoff
Recorrendo à placa de ligações, proceda à montagem do circuito cujo esquema se indica na
figura 6. Use 4 resistências iguais, com valor compreendido entre 100 Ω e 1 kΩ e regule o gerador
para 10 V. Na figura indicam-se um voltímetro e um amperímetro que vai utilizar nas medidas.
Note o aspecto final do circuito que se indica à direita da figura.
A
V
R1 = R2 = R3 = R4
E = 10 V
Figura 6. Esquema e esboço de circuito para estudar as leis de Kirchoff
2.3.1. Utilizando o voltímetro digital, meça as quedas de tensão sobre as 4 resistências, tendo o
cuidado de colocar as pontas vermelha e preta nos terminais assinalados de + e - (no
esquema), respectivamente. Registe os valores na tabela 3 da folha de registo de dados.
2.3.2. Utilizando agora o amperímetro digital, meça as intensidades das 3 correntes marcadas no
esquema. Para tal deve soltar da placa o terminal da resistência do lado onde está marcada a
seta e intercalar o aparelho com a ponta preta a tocar no terminal solto e a ponta vermelha a
tocar no ponto anterior à seta. Registe os valores na tabela 3 da folha de registo de dados.
3. Tratamento dos dados
3.1. Verificação experimental da lei de Ohm
3.1.1. Construa o gráfico da Tensão em função da Corrente. Trace a recta que melhor se ajusta aos
pontos experimentais, referindo no seu relatório o método que usou para o traçado. Inclua o
gráfico em anexo ao relatório.
3.1.2. A partir das características da recta traçada obtenha o valor da resistência.
Na análise dos resultados compare o valor obtido com o marcado na resistência, determinando
o erro relativo percentual. Explique a razão dos erros encontrados.
3.2. Determinação da resistência interna de pilhas comerciais
3.2.1. Comece por completar a tabela 2 da folha de "registo de dados e cálculos", efectuando a
determinação dos valores da corrente Icalculada. Devem estes obedecer à equação: Ic = VAB/R.
Departamento de Física da FCTUC
5/7
Física Laboratorial I
Ano Lectivo 2008/09
3.2.2. Construa o gráfico da tensão VAB em função da corrente I para cada uma das pilhas.
Compare os gráficos obtidos com o representado na fig. 2-b) e, utilizando apenas os pontos
em que o comportamento da pilha pode ser aproximado por uma fonte de tensão real
(andamento linear), determine a resistência interna da pilha.
Na análise dos resultados compare os valores obtidos para cada uma das pilhas e comente.
3.3. Verificação experimental das leis de Kirchoff
3.3.1. Usando a lei dos nodos e a lei das malhas, calcule as intensidades das 3 correntes marcadas na
figura 6. De seguida calcule as d.d.p.s através de cada uma das resistências; chame-lhes V1,
V2, V3 e V4.
Apresente todos os cálculos que efectuar na parte de "tratamento matemático dos dados
experimentais" do seu relatório.
Na análise dos resultados compare os valores medidos experimentalmente com os obtidos por
cálculo, determinando o erro relativo percentual de cada valor. Aponte origens para a
imprecisão dos valores.
3.3.2. Note que no circuito esquematizado na figura 6 as resistências R2 e R4 estão em série e, por
sua vez o conjunto de ambas está em paralelo com a resistência R3.
Comece por calcular a resistência equivalente a R2 + R4. De seguida faça o produto dessa
resistência pela intensidade da corrente I2.
Na análise dos resultados compare a d.d.p. assim obtida com a soma de V2 + V4 e comente.
3.3.3. Calcule a resistência equivalente ao paralelo de (R2 + R4) com R3. De seguida faça o produto
dessa resistência pela intensidade da corrente I1.
Na análise dos resultados compare a d.d.p. assim obtida, primeiro com a soma de V2 + V4 e
depois com V3. Comente os dois casos.
4. Relatório
Elabore um relatório do trabalho efectuado, seguindo as directivas que lhe foram propostas. No
ponto de análise dos resultados obtidos deve seguir as recomendações indicadas em § 3.
Bibliografia
[1] M.M.R.R. Costa e M.J.B.M. de Almeida, Fundamentos de Física, 2ª edição, Coimbra, Livraria
Almedina (2004).
[2] Paul Tipler, Física, Editora Guanabara-Koogan, 4ª Edição (2000).
[3] M. Alonso e E. Finn, Física, Addison-Wesley Iberoamericana (1999)
[4] Introdução à análise de dados nas medidas de grandezas físicas, Coimbra, Departamento de
Física da Universidade (2005/06).
[5] M.C. Abreu, L. Matias e L.F. Peralta, Física Experimental - Uma introdução, Lisboa, Editorial
Presença (1994).
Departamento de Física da FCTUC
6/7
Física Laboratorial I
Ano Lectivo 2008/09
P6 - RESISTÊNCIA E CIRCUITOS ELÉCTRICOS
Alunos
Visto do Professor
_______________
REGISTO DE DADOS E CÁLCULOS
2.1. Verificação experimental da lei de Ohm
§ 2.1.1. Resistência usada: R = ________ Ω e Pmáx ≤ 0,5 W ⇒ Vmáx ≤ ________ V
Tabela 1. Leituras de tensão e corrente para verificação da lei de Ohm
Tensão (V)
Vmáx
Corrente (A)
2.2. Determinação da resistência interna de pilhas comerciais
Tabela 2. Valores de tensão medidos e intensidades de corrente calculadas para cada pilha
Pilha Alcalina
Pilha Zinco-Carvão
E (V) =
E (V) =
R (Ω)
VAB (V)
Icalculada (A)
VAB (V)
Icalculada (A)
100
50
30
20
15
10
5
3
2
1
2.3. Verificação experimental das leis de Kirchoff
Tabela 3. Valores de tensão e corrente no circuito
Resistências usadas
V1 (V)
V2 (V)
V3 (V)
I1 (mA)
I2 (mA)
I3 (mA)
V4 (V)
R = ________ Ω
Departamento de Física da FCTUC
7/7