Inversões Termo de uma matriz

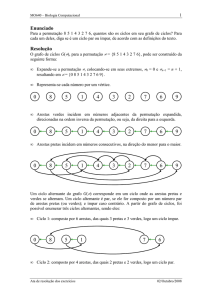
Inversões
➢ Cada conjunto de números admite tantas permutações quantas as ordens pelas quais
podem ser apresentados.
➢ O factorial (n!) é o produto de um elemento por todos os que o antecedem e dá-nos o
número de permutações possível (com n elementos podemos formar n! permutações).
➢ Ao nível dos números naturais, diz-se que Π0 =1,2,3,4,...,n é a permutação
principal.
➢ Considerando uma permutação e comparando-a com a permutação principal, diz-se
que dois números formam:
» uma permanência quando não se alterou a ordem
» uma inversão quando a sua ordem foi alterada
M atem ática (CU RSO : Gestão da Q ualidade)
1
Termo de uma matriz
➢ Permutação par - quando o número de inversões é par.
➢ Permutação ímpar - quando o número de inversões é impar.
➢ Seja A uma matriz de ordem n.
Termo da matriz A - o produto de n elementos onde entra como factor um e um só
elemento de cada linha e um e um só elemento de cada coluna.
➢ Os termos de uma matriz podem ser:
» Pares - quando as permutações das linhas e das colunas apresentam um número
par de inversões.
» Ímpares - quando as permutações das linhas e das colunas apresentam um
número ímpar de inversões.
M atem ática (CU RSO : Gestão da Q ualidade)
2