trabalho 81 - RNC -PULSOS DO TIPO SÓLITON EM FIBRAS ÓPTICAS

PULSOS DO TIPO SÓLITON EM FIBRAS ÓPTICAS
Nome Renato Juliani Ribamar Vieira1, Regina Maria Ricotta2
1,2
Faculdade de Tecnologia de São Paulo – FATEC-SP
[email protected], [email protected]
1. Introdução
Desde a primeira observação de uma onda solitária,
feita por Russell, em 1834, na forma de uma onda aquática [1], as ondas não-lineares têm fascinado cientistas
do mundo inteiro.
Do ponto de vista matemático, sólitons são soluções
de equações diferenciais, não-lineares integráveis. Do
ponto de vista prático, são ondas capazes de se propagarem com forma inalterada por distâncias muito elevadas, através do balanceamento entre a não-linearidade
juntamente com termos de derivadas superior.
Por este motivo, foi proposto que sólitons pudessem
ser utilizados em telecomunicações, e a partir de então,
vários desenvolvimentos tecnológicos foram realizados
para sua propagação via fibras ópticas [2].
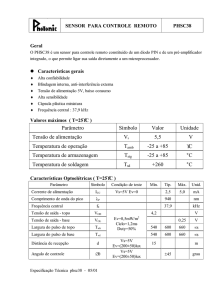
pelo pulso. A Figura 1 mostra as formas de dois pulsos
após se propagarem por 125 e 310km por um guia
óptico. Note que após 310km o pulso linear é
completamente irresolvível.
2. Propagação do pulso via fibras ópticas
No sistema de comunicação digital, a informação
enviada é primeiramente codificada na forma de pulsos
luminosos e transmitida por um transmissor (fibra
óptica) para um receptor, onde a informação é
decodificada. Dessa forma, quanto maior a quantidade
de pulsos que podem ser enviados em um intervalo de
tempo, e ainda serem determinados pelo receptor, maior
será a capacidade de transmissão do sistema [3].
Entretanto, existem efeitos que induzem a um
alargamento do pulso luminoso que se propaga em uma
fibra óptica. Assim, nos sistemas de comunicação
atuais, os sinais devem ser regenerados para assegurar
que a informação seja inteiramente captada pelo
receptor; processo realizado por regeneradores ou
repetidores de sinais.
São dois os efeitos sofridos pelo pulso que se destacam:
- O efeito dispersivo (GVD – dispersão de
velocidade de grupo) ocorre devido à dependência de
cada comprimento de onda do pulso, que se propaga
pela fibra, com o índice de refração do meio. Dessa
forma, cada componente espectral do pulso apresentará
uma velocidade, gerando um alargamento do envelope
do pulso. Um pulso com estas características terá a
freqüência instantânea dependente do tempo; para este
efeito dá-se o nome de chirp.
- O efeito não-linear da automodulação de fase
(SPM) ocorre devido à variação do índice de refração
como função da intensidade em um meio óptico não
linear. Esse fenômeno leva a um alargamento espectral
do pulso, mantendo a forma temporal inalterada.
Através de um estudo dos efeitos combinados das
freqüências induzidas pela dispersão da velocidade de
grupo (GVD) e automodulação de fase (SPM), pode-se
ter um balanceamento destes efeitos de forma a produzir
uma onda estável (sóliton). Esta compensação pode ser
alcançada através de uma escolha adequada da forma do
pulso (uma secante hiperbólica) e da potência carregada
Fig.1 – Forma de um pulso do tipo sóliton e um linear
após se propagarem por um guia óptico.
A evolução de um pulso óptico se propagando
através de um meio dispersivo não-linear é
aproximadamente governada pela equação de
Schrödinger não-linear (NLSE):
 ∂f
1 ∂f  1
∂2 f
 − α
− i 
+
+ Γ f
vg ∂ t  2
∂t 2
 ∂z
2
f = 0
(1)
com α sendo o termo de dispersão e Γ o termo de nãolinearidade.
3. Conclusão
Mesmo com as vantagens de não ser necessária a
utilização de regeneradores de sinais, e oferecer altas
taxas de transmissão ao se utilizar pulsos do tipo sóliton,
o custo das fibras ópticas com as propriedades
dielétricas desejadas é um fator que pesa contra a
utilização destes pulsos. Por este motivo ainda não são
utilizados em telecomunicação. Evidentemente, os
sinais do tipo sóliton somente irão prevalecer caso
ofereçam altas taxas de transmissão a baixos custos.
4. Referências
[1] R.L. Herman, Soliton Propagation in Optical Fibers.
http://people.unew.ed/hermanr/research/solitons/html
[2] W. Galléas, L.H. Ymai, P.L. Natti, E.R. Takano
Natti, Rev. Bras. Ens. Fis., V.25, n.3 (2003).
[3] A.Ghatak and K. Thyagarajam, Introduction to Fiber
Optics, Cambridge University Press, 1998.
1
Aluno de IC do CNPq.