Movimentos-verticais-e-gráficos-resolvida

Movimentos verticais e Gráficos
1. Deixa-se cair um objeto de massa 500 g de uma altura de 5m acima do solo. Assinale a
alternativa que representa a velocidade do objeto, imediatamente, antes de tocar o solo,
desprezando-se a resistência do ar.
a) 10m / s
b) 7,0m / s
c) 5,0m / s
d) 15m / s
e) 2,5m / s
2. Vários corpos idênticos são abandonados de uma altura de 7,20m em relação ao solo, em
intervalos de tempos iguais. Quando o primeiro corpo atingir o solo, o quinto corpo inicia seu
movimento de queda livre. Desprezando a resistência do ar e adotando a aceleração da
gravidade g  10,0 m / s2 , a velocidade do segundo corpo nessas condições é
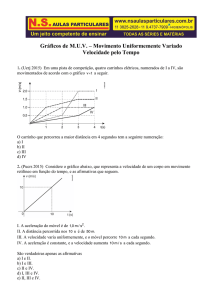
a) 10,0 m / s
b) 6,0 m / s
c) 3,0 m / s
d) 9,0 m / s
e) 12,0 m / s
3. Um paraquedista salta de um avião e cai livremente por uma distância vertical de 80m,
antes de abrir o paraquedas. Quando este se abre, ele passa a sofrer uma desaceleração
vertical de 4m / s2, chegando ao solo com uma velocidade vertical de módulo 2m / s. Supondo
que, ao saltar do avião, a velocidade inicial do paraquedista na vertical era igual a zero e
considerando g  10m / s2 , determine:
a) O tempo total que o paraquedista permaneceu no ar, desde o salto até atingir o solo.
b) A distância vertical total percorrida pelo paraquedista.
4. Um astronauta, em um planeta desconhecido, observa que um objeto leva 2,0 s para cair,
partindo do repouso, de uma altura de 12 m.
A aceleração gravitacional nesse planeta, em m / s2 é:
a) 3,0
b) 6,0
c) 10
d) 12
e) 14
5. Um corpo A é abandonado de um ponto situado a 10 metros acima do solo. No mesmo
instante, um corpo B é lançado verticalmente de baixo para cima com velocidade v 0 suficiente
para que possa atingir 10 metros de altura.
Página 1 de 20
Desprezando a resistência do ar, chamando respectivamente v A e v B as velocidades de A e
B quando se encontram a 5 metros de altura, o valor da razão v A vB , em módulo é
a) 4
b) 2
c) 1
d) 1 2
6. Dois corpos A e B de massas mA  1,0 kg e mB  1,0  103 kg, respectivamente, são
abandonados de uma mesma altura h, no interior de um tubo vertical onde existe o vácuo. Para
percorrer a altura h,
a) o tempo de queda do corpo A é igual que o do corpo B.
b) o tempo de queda do corpo A é maior que o do corpo B.
c) o tempo de queda do corpo A é menor que o do corpo B.
d) o tempo de queda depende do volume dos corpos A e B.
e) o tempo de queda depende da forma geométrica dos corpos A e B.
7. Um corpo de massa m é largado de certa altura. Considerando que g  10 m / s2 e
desprezando o atrito do ar, podemos afirmar que após um tempo de 2,5 segundos a distância
percorrida pelo corpo e a sua velocidade são iguais, respectivamente, a
a) 12,5 m; 12,5 m / s
b) 31,25 m; 12,5 m / s
c) 125 m; 12,5 m / s
d) 6,25 m; 2,5 m / s
e) 31,25 m; 25 m / s
8. Uma ave marinha costuma mergulhar de uma altura de 20 m para buscar alimento no mar.
Suponha que um desses mergulhos tenha sido feito em sentido vertical, a partir do repouso e
exclusivamente sob ação da força da gravidade.
Desprezando-se as forças de atrito e de resistência do ar, a ave chegará à superfície do mar a
uma velocidade, em m/s, aproximadamente igual a:
a) 20
b) 40
c) 60
d) 80
9. A castanha-do-pará (Bertholletia excelsa) é fonte de alimentação e renda das populações
tradicionais da Amazônia. Sua coleta é realizada por extrativistas que percorrem quilômetros
de trilhas nas matas, durante o período das chuvas amazônicas. A castanheira é uma das
maiores árvores da floresta, atingindo facilmente a altura de 50m. O fruto da castanheira, um
ouriço, tem cerca de 1kg e contém, em média, 16 sementes. Baseando-se nesses dados e
Página 2 de 20
considerando o valor padrão da aceleração da gravidade 9,81m / s2 , pode-se estimar que a
velocidade com que o ouriço atinge o solo, ao cair do alto de uma castanheira, é de, em m / s,
aproximadamente,
a) 5,2.
b) 10,1.
c) 20,4.
d) 31,3.
e) 98,1.
TEXTO PARA A PRÓXIMA QUESTÃO:
Considere os dados abaixo para resolver a(s) questão(ões) quando for necessário.
Constantes físicas
Aceleração da gravidade: g  10 m / s2
Densidade da água: r  1,0 g / cm3
10. Uma garota lança uma pedra verticalmente para cima. Sendo a, o módulo da aceleração
e v, o módulo da velocidade da mesma, no ponto mais alto de sua trajetória, é correto afirmar
que v é ___________ a (de) zero, se a for ___________ a (de) zero.
Os termos que completam de forma correta e, respectivamente, as lacunas são
a) igual, igual
b) igual, diferente
c) diferente, igual
d) diferente, diferente
11. Dois veículos, A e B, partem simultaneamente de uma mesma posição e movem-se no
mesmo sentido ao longo de uma rodovia plana e retilínea durante 120 s. As curvas do gráfico
representam, nesse intervalo de tempo, como variam suas velocidades escalares em função do
tempo.
Calcule:
a) o módulo das velocidades escalares médias de A e de B, em m s, durante os 120 s.
b) a distância entre os veículos, em metros, no instante t  60 s.
TEXTO PARA A PRÓXIMA QUESTÃO:
Se necessário, use
aceleração da gravidade: g  10 m / s2
Página 3 de 20
densidade da água: d  1,0 kg / L
calor específico da água: c  1cal / g C
1cal  4 J
constante eletrostática: k  9 ,0  109 N  m2 / C2
constante universal dos gases perfeitos: R  8 J / mol  K
12. Dois móveis, A e B, partindo juntos de uma mesma posição, porém com velocidades
diferentes, que variam conforme o gráfico abaixo, irão se encontrar novamente em um
determinado instante.
Considerando que os intervalos de tempo t1  t0 , t2  t1, t3  t 2 , t 4  t3 e t5  t 4 são todos
iguais, os móveis A e B novamente se encontrarão no instante
a) t 4
b) t 5
c) t 2
d) t 3
13. Considere o gráfico abaixo, que representa a velocidade de um corpo em movimento
retilíneo em função do tempo, e as afirmativas que seguem.
I. A aceleração do móvel é de 1,0 m / s2 .
II. A distância percorrida nos 10 s é de 50 m.
III. A velocidade varia uniformemente, e o móvel percorre 10 m a cada segundo.
IV. A aceleração é constante, e a velocidade aumenta 10 m / s a cada segundo.
São verdadeiras apenas as afirmativas
a) I e II.
b) I e III.
c) II e IV.
d) I, III e IV.
Página 4 de 20
e) II, III e IV.
14. Um veículo está se movendo ao longo de uma estrada plana e retilínea. Sua velocidade
em função do tempo, para um trecho do percurso, foi registrada e está mostrada no gráfico
abaixo. Considerando que em t  0 a posição do veículo s é igual a zero, assinale a
alternativa correta para a sua posição ao final dos 45s.
a)
b)
c)
d)
e)
330m.
480m.
700m.
715m.
804m.
15. Considere um carro que se movimenta ao longo de uma pista retilínea. O gráfico abaixo
descreve a velocidade do carro em função do tempo, segundo um observador em repouso
sobre a calçada.
Em relação a essa situação, assinale a alternativa correta.
a) O movimento é uniformemente variado.
b) O carro realiza um movimento retilíneo uniforme.
c) Ao final do movimento (t  8s), o carro retorna à sua posição de origem (t  0).
d) O carro está freando no intervalo 4s  t  8s.
e) Em t  4, o carro inverte o sentido do seu movimento.
16. O deslocamento Δx de uma partícula em função do tempo t é ilustrado no gráfico a
seguir:
Página 5 de 20
Com relação ao movimento mostrado no gráfico, assinale a alternativa CORRETA.
a) A partícula inicia seu movimento com velocidade constante; na sequência, o movimento é
acelerado e, finalmente, a partícula se move com outra velocidade também constante.
b) A velocidade da partícula é constante.
c) A aceleração da partícula é constante.
d) Esse gráfico ilustra o movimento de queda livre de um objeto nas proximidades da superfície
terrestre, onde a resistência do ar foi desprezada.
e) A partícula inicia seu movimento com uma velocidade não nula, mas o movimento é
retardado, e ela finalmente atinge o repouso.
17. Os dois primeiros colocados de uma prova de 100 m rasos de um campeonato de
atletismo foram, respectivamente, os corredores A e B. O gráfico representa as velocidades
escalares desses dois corredores em função do tempo, desde o instante da largada (t = 0) até
os instantes em que eles cruzaram a linha de chegada.
Analisando as informações do gráfico, é correto afirmar que, no instante em que o corredor A
cruzou a linha de chegada, faltava ainda, para o corredor B completar a prova, uma distância,
em metros, igual a
a) 5.
b) 25.
c) 15.
d) 20.
e) 10.
18. Um objeto tem a sua posição (x) em função do tempo (t) descrito pela parábola conforme
o gráfico.
Página 6 de 20
Analisando-se esse movimento, o módulo de sua velocidade inicial, em m/s, e de sua
aceleração, em m/s2, são respectivamente iguais a
a) 10 e 20.
b) 10 e 30.
c) 20 e 10.
d) 20 e 30.
e) 30 e 10.
19. Dois móveis A e B deslocam-se em uma trajetória retilínea, com acelerações constantes e
positivas. Considerando que a velocidade inicial de A é menor do que a de B (v A  vB ) e que
a aceleração de A é maior do que a de B (aA  aB ), analise os gráficos a seguir.
O gráfico que melhor representa as características mencionadas é o:
a) A.
b) B.
c) C.
Página 7 de 20
d) D.
e) E.
20. Uma pessoa do alto de um prédio solta uma bola e mede o módulo da posição da bola em
função do tempo. A figura, abaixo, mostra o esboço do gráfico da posição em relação ao
tempo.
Assinale a alternativa que representa o esboço dos gráficos em relação à velocidade  tempo
e à aceleração  tempo, respectivamente.
a)
b)
c)
Página 8 de 20
d)
e)
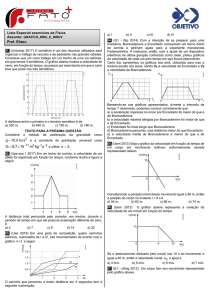
21. O gráfico abaixo representa a variação da velocidade dos carros A e B que se deslocam
em uma estrada.
Determine as distâncias percorridas pelos carros A e B durante os primeiros cinco segundos do
percurso. Calcule, também, a aceleração do carro A nos dois primeiros segundos.
22. Com a intenção de se preparar para uma maratona, Brancadeneve e Encantado
começaram um treino diário de corrida e pediram ajuda para a experiente maratonista
Fadamadrinha. A instrutora, então, com a ajuda de um dispositivo eletrônico de última geração
conhecido como radar, plotou gráficos da velocidade de cada um pelo tempo em que ficava
observando.
Certo dia, apresentou os gráficos aos dois, utilizando para isso a mesma escala nos eixos,
sendo VE a velocidade de Encantado e VB a velocidade de Brancadeneve.
Página 9 de 20
Baseando-se nos gráficos apresentados, durante o intervalo de tempo T observado, podemos
concluir corretamente que
a) a aceleração impressa no início por Encantado foi maior do que a de Brancadeneve.
b) a velocidade máxima atingida por Brancadeneve foi maior do que a de Encantado.
c) Encantado foi mais longe que Brancadeneve.
d) Brancadeneve percorreu uma distância maior do que Encantado.
e) a velocidade média de Brancadeneve é menor do que a de Encantado.
23. Um motorista dirigia por uma estrada plana e retilínea quando, por causa de obras, foi
obrigado a desacelerar seu veículo, reduzindo sua velocidade de 90 km/h (25 m/s) para 54
km/h (15 m/s). Depois de passado o trecho em obras, retornou à velocidade inicial de 90 km/h.
O gráfico representa como variou a velocidade escalar do veículo em função do tempo,
enquanto ele passou por esse trecho da rodovia.
Caso não tivesse reduzido a velocidade devido às obras, mas mantido sua velocidade
constante de 90 km/h durante os 80 s representados no gráfico, a distância adicional que teria
percorrido nessa estrada seria, em metros, de
a) 1 650.
b) 800.
c) 950.
d) 1 250.
e) 350.
Página 10 de 20
Gabarito:
Resposta da questão 1:
[A]
Sabendo que se trata de uma queda livre (velocidade inicial v 0 é nula), onde a altura inicial é
de 5 metros e a massa do corpo é de 0,5 kg, podemos resolver de duas formas distintas.
1ª Solução – Queda Livre:
Utilizando a equação de Torricelli, temos que:
v2  v02  2  a  ΔS
Onde,
ag
ΔS  h
v0  0
Temos que,
v2  2  g  h
v 2  2  10  5
v  100
v  10 m s
2ª Solução – Conservação de Energia Mecânica:
Sabendo que inicialmente o corpo está em repouso, podemos dizer que:
Em  Em
i
f
Ep  Ec
gi
m gh 
f
m  v2
2
v2  2  g  h
v  10 m s
Resposta da questão 2:
[D]
Calculando o tempo de queda:
h
1 2
g t q  tq 
2
2h

g
2  7,2 
10
 1,44  t q  1,2 s.
A figura mostra os cinco corpos e o tempo (t) de movimento de cada um deles.
Página 11 de 20
A velocidade do 2º corpo é:
v  v 0  g t  v  0  10  0,9  
v  9 m/s.
Resposta da questão 3:
a) Tempo total do salto até atingir o solo: t  t1  t 2
No primeiro momento, na queda livre do paraquedista.
ΔS1  v o  t 
80 
a  t12
2
10  t12
2
t12  16
t1  4 s
Encontrando a velocidade no final do primeiro momento,
v1  v o  a  t1
v1  10  4
v1  40 m s
Assim, achando o tempo do segundo momento, temos que:
v 2  v1  a  t 2
2  40  4  t 2
t 2  9,5 s
Por fim, o tempo total será:
t  t1  t 2  4  9,5
t  13,5 s
b) A distância total percorrida: ΔSt  ΔS1  ΔS2
A distância percorrida no primeiro momento foi dada no enunciado (80 m). Para o segundo
momento, temos que:
v 22  v12  2  a  ΔS2
22  402  2   4   ΔS2
402  22
8
ΔS2  199,5 m
ΔS2 
Página 12 de 20
Logo,
ΔSt  80  199,5
ΔSt  279,5 m
Resposta da questão 4:
[B]
Com a equação da altura em função do tempo do movimento de queda livre, calculamos a
aceleração.
gt 2
2h
g
2
t2
2  12 m
g
 6 m / s2
2
 2 s
h
Resposta da questão 5:
[C]
Temos situações semelhantes para os dois corpos, pois ambos percorrem 5 m com as
mesmas acelerações sendo que as condições de contorno também são similares, logo as
velocidades em módulo serão iguais e sua razão será 1.
Outra possibilidade é calcular usando os conhecimentos de lançamento vertical e queda livre.
Para o corpo A, que cai em queda livre, usando o referencial positivo para baixo e a equação
de Torricelli:
v 2  v02  2gΔh  v  v02  2gΔh
v A  02  2  10  5  v  10 m / s
Para o corpo B, que sobe na vertical, usando o referencial positivo para cima, primeiramente
descobrimos a velocidade inicial e depois a velocidade na posição de 5 m :
v2  v02  2gΔh  v0  v2  2gΔh
v0  02  2  10  10  v0  10 2 m s
E a intensidade da velocidade a 5 m de altura:
vB 
Então,
10 2 
2
 2  10  5  v  10 m / s
v A 10

 1.
vB 10
Resposta da questão 6:
[A]
Se o corpo está em queda livre, a resultante das forças sobre ele é seu próprio peso. Aplicando
a segunda lei de Newton a essa situação:
R  P  m a  m g  a  g.
A aceleração de queda independe da massa e é igual a aceleração da gravidade. Calculando o
Página 13 de 20
tempo de queda:
h
g 2
t  t
2
2h
.
g
Consequentemente, o tempo de queda também independe da massa. Portanto, o tempo de
queda é o mesmo para os dois corpos.
Resposta da questão 7:
[E]
A distância percorrida em queda livre é dada por:
h
g  t2
2
Logo,
10 m / s2   2,5 s 
2
h
2
 h  31,25 m
Já a velocidade é dada por:
v  v0  g  t
v  0  10 m / s2  2,5 s  v  25 m / s
Resposta da questão 8:
[A]
Usando a equação de Torricelli com a = g = 10 m/s2 e ΔS  h  20m.
v 2  v 02  2g h  v 2  0  2  10  20  400 
v  20 m/s.
Resposta da questão 9:
[D]
Aplicando a equação de Torricelli à queda livre, temos:
v2  2 gh  v 
2 g h  2  9,81 50 
981 
v  31,3 m/s.
Resposta da questão 10:
[B]
No lançamento vertical, no ponto mais alto a velocidade é igual a zero e a aceleração é igual à
da gravidade, diferente de zero, supondo que a garota em questão esteja na Terra ou em
outro qualquer lugar do universo onde haja gravidade.
Resposta da questão 11:
a) Sabendo que em um gráfico da velocidade pelo tempo, tem-se que:
Área  ΔS
Assim, podemos calcular o deslocamento escalar dos dois veículos durante o intervalo de
tempo total:
Página 14 de 20
b  h 120  20

2
2
ΔS A  1200 m
ΔS A 
b  h 120  20

2
2
ΔSB  1200 m
ΔSB 
Como o intervalo de tempo e o deslocamento é o mesmo para os dois veículos, as
velocidades médias deles também são iguais. Assim,
ΔS2 1200
v1  v 2 

Δt 2
120
v1  v 2  10 m s
b) Para encontrarmos a distância entre os veículos é necessário encontrar o espaço que eles
ocupam no instante 60 segundos.
Para tanto, é necessário encontrar a velocidade dos móveis nesse ponto.
Analisando o veículo A, temos que:
ΔVa 0  20
aA 

Δt
100
a A  0,2 m s2
Com o valor da aceleração, podemos encontrar a velocidade do veículo A:
va  va  aA  t
60
20
va
60
va
60
 20   0,2  40
 12 m s
Note que, em comparação ao veículo A, a aceleração do veículo B tem mesmo módulo e
sentido contrário e a velocidade tem o mesmo módulo.
Assim,
ΔS A '  A Triangulo  A trapézio
20  20  20  12   40

2
2
ΔS A '  200  640
ΔS A ' 
ΔS A '  840 m
e
ΔSB '  A Triangulo 
60  12
2
ΔSB '  360 m
Sendo d a distância entre os veículos no instante 60 segundos,
d  ΔS A ' ΔSB '  840  360
d  480 m
Resposta da questão 12:
[A]
Página 15 de 20
O móvel B começa com maior velocidade em relação ao móvel A inicialmente e, portanto como
a distância percorrida representa a área sob a curva v  t, a área pintada de amarelo
representa a vantagem percorrida por B em relação à A até o momento t 2 quando as
velocidades dos dois móveis passam a ser iguais (área A1), a partir do qual com o móvel B
desacelerando e o móvel A acelerando com o mesmo módulo. Como os móveis acabam
invertendo as velocidades, agora é o móvel A que começa a percorrer maior distância com o
tempo e a área pintada de azul representa a vantagem de A em relação à B (área A 2 ).
Para que os dois móveis se encontrem novamente estas áreas devem ser iguais, portanto o
encontro se dá no tempo t 4 .
Resposta da questão 13:
[A]
[I] Verdadeira. Aplicando a definição de aceleração escalar média:
Δv 10
a  am 

 a  1 m/s2.
Δt 10
[II] Verdadeira. O espaço percorrido é dado pela área entre a linha do gráfico e o eixo dos
tempos.
10  10
ΔS 
 ΔS  50 m.
2
[III] Falsa. A velocidade é variável.
[IV] Falsa. A velocidade aumenta 1,0 m/s a cada segundo.
Resposta da questão 14:
[D]
Como a posição inicial é zero, a sua posição final será exatamente igual à distância percorrida.
Sabendo que a distância percorrida é igual numericamente à área do gráfico, então:
Página 16 de 20
ΔST  A1  A2  A3  A4  A5
Porém, para que seja possível calcular as áreas 4 e 5, é necessário encontrar o tempo em que
acontece a mudança de sentido na velocidade (ponto em que cruza o eixo x).
Sabendo que o movimento de 1 para 2 é um Movimento Retilíneo Uniformemente Variado
(MRUV), podemos analisar este intervalo de tempo para encontrar a aceleração.
v  v 0  at
10  36  a  5
a  9,2 m s
Agora, analisando o trecho de 1 para 3, temos que:
v  v 0  at
0  36  9,2  t
t 3,9 s
Assim,
 15  5   28   10  28   3,9  36    6,1  5   10 
ΔST   35  8   




2
2

  2   2  

ΔST  280  280  140  70,2  55,5
ΔST  714,7 m
ΔST
715 m
Resposta da questão 15:
[D]
Analisando as alternativas,
[A] INCORRETA. Em um movimento uniformemente variado, a aceleração é constante durante
o movimento. O Gráfico mostra claramente que na primeira parte do movimento o módulo
da velocidade está aumentando (aceleração maior que zero) e na segunda parte diminuindo
(aceleração menor que zero). Desta forma, pode-se dizer que a aceleração não é constante
durante o movimento.
[B] INCORRETA. Um movimento retilíneo uniforme tem aceleração nula.
[C] INCORRETA. Em momento algum do movimento descrito na figura existe uma inversão de
sentido do movimento. Logo, o carro não irá retornar a sua posição inicial.
[D] CORRETA.
[E] INCORRETA. Inverte o sentido de sua aceleração e não do movimento (velocidade).
Resposta da questão 16:
[E]
No gráfico do espaço em função do tempo, a declividade da curva nos dá a velocidade escalar.
Ou seja, a velocidade escalar é numericamente igual a tangente do ângulo que a curva faz com
o eixo dos tempos.
Página 17 de 20
Assim:
v0  tg α0  0; v1  tg α1 .
Analisando o gráfico, vemos que a declividade vai diminuindo, até que em t  4 s  α 4  0,
quando a velocidade se anula. Portanto, o movimento é retardado com velocidade final nula.
Resposta da questão 17:
[D]
O corredor A termina a prova em t = 10 s e o corredor B em t = 12 s. De 10 s a 12 s, B teve
velocidade de 10 m/s, percorrendo:
d  vB Δt  10 12  10  
d  20 m.
Resposta da questão 18:
[C]
Dados do gráfico: x0  0; t  2s  (v  0 e x  20m).
Como o gráfico é um arco de parábola, trata-se de movimento uniformemente variado (MUV).
Usando, então, as respectivas equações:
v  v 0  a t  0  v 0  a  2   v 0  - 2 a I

t2s 
a 2
a 2
 x  v 0 t  t  20  v 0  2    2   20  2 v 0  2 a II

2
2
(I) em (II):
20  2  2a   2 a
 2 a   20

a  10 m/s2.
Em (I):
v0   2 a  v0   2  10  
v 0  20 m/s.
Resposta da questão 19:
[D]
Nota: há uma imprecisão gramatical no enunciado, afirmando (no singular) que os dois móveis
têm aceleração constante. É, então, de se supor que as acelerações sejam iguais. Porém, logo
a seguir, afirma-se que aA  aB . Para que se evitem confusões, o enunciado na primeira linha
deveria ser:
“Dois móveis A e B deslocam-se em uma trajetória retilínea, com acelerações constantes e..."
Mas, vamos à resolução.
Como as acelerações (escalares) são constantes e positivas, os gráficos das velocidades são
trechos de reta ascendentes. Sendo aA  aB , o segmento referente à velocidade do móvel A
tem maior declividade, começando num ponto abaixo do de B, pois v A  vB . Essas
conclusões, levam-nos ao Gráfico D.
Resposta da questão 20:
[A]
Considerando desprezível a resistência do ar, a bola desce em queda livre até que, num
determinado instante, ela para abruptamente.
Página 18 de 20
Assim, a velocidade escalar aumenta linearmente com o tempo, anulando-se
instantaneamente, enquanto que a aceleração escalar é constante, até se anular, também,
instantaneamente, como mostram os gráficos da alternativa [A].
Resposta da questão 21:
 Distâncias percorridas pelos carros:
No gráfico v  t a distância percorrida é numericamente igual à área entre a linha do gráfico e o
eixo dos tempos. Assim:
53

DA  2  2  DA  8 m.


D   4  1  2    3  1  D  8 m.
B

 A  2


 Aceleração do carro A:
Dados: v0 = 0; v = 2 m/s; Δt  2s.
Entendendo por aceleração apenas a aceleração escalar do veículo, temos:
Δv 2  0
a

 a  1 m/s2 .
Δt
2
Resposta da questão 22:
[D]
Tomando como unidade (u) o lado de cada quadrículo, e usando a propriedade do gráfico da
velocidade  tempo, as áreas dos trapézios fornecem as distâncias percorridas por Encantado
(dE) e Brancadeneve (dB):

5 1
dE  2  4  dE  12 u.

d  6  4  3  d  15 u.
B
 B
2

dB  dE.
Resposta da questão 23:
[E]
A distância (D) pedida é numericamente igual à área hachurada no gráfico.
D
50  20
 10  D  350 m.
2
Página 19 de 20
Página 20 de 20