Arquivo 1 - Colégio Fato Mais

Lista Especial exercícios de Física
Assunto: GRAFICO_MRU_E_MRUV
Prof. Elizeu
a) I
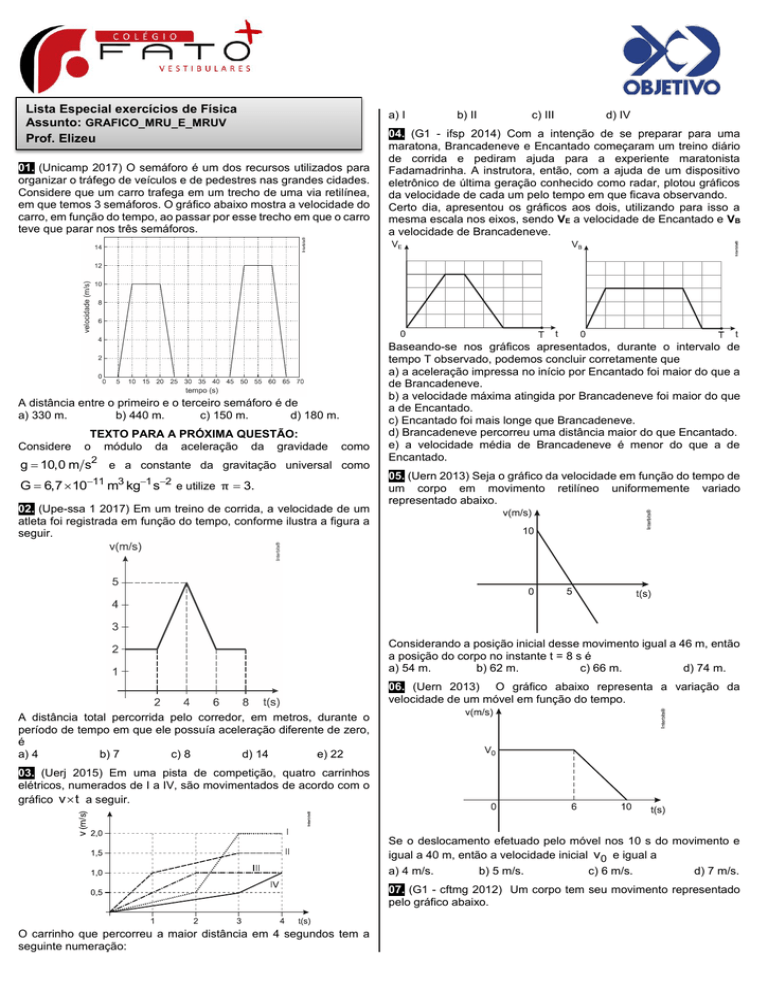
01. (Unicamp 2017) O semáforo é um dos recursos utilizados para
organizar o tráfego de veículos e de pedestres nas grandes cidades.
Considere que um carro trafega em um trecho de uma via retilínea,
em que temos 3 semáforos. O gráfico abaixo mostra a velocidade do
carro, em função do tempo, ao passar por esse trecho em que o carro
teve que parar nos três semáforos.
A distância entre o primeiro e o terceiro semáforo é de
a) 330 m.
b) 440 m.
c) 150 m.
d) 180 m.
Considere
TEXTO PARA A PRÓXIMA QUESTÃO:
o módulo da aceleração da gravidade
2
g  10,0 m s
11
G  6,7  10
como
e a constante da gravitação universal como
m3 kg1 s2 e utilize π  3.
02. (Upe-ssa 1 2017) Em um treino de corrida, a velocidade de um
atleta foi registrada em função do tempo, conforme ilustra a figura a
seguir.
b) II
c) III
d) IV
04. (G1 - ifsp 2014) Com a intenção de se preparar para uma
maratona, Brancadeneve e Encantado começaram um treino diário
de corrida e pediram ajuda para a experiente maratonista
Fadamadrinha. A instrutora, então, com a ajuda de um dispositivo
eletrônico de última geração conhecido como radar, plotou gráficos
da velocidade de cada um pelo tempo em que ficava observando.
Certo dia, apresentou os gráficos aos dois, utilizando para isso a
mesma escala nos eixos, sendo VE a velocidade de Encantado e VB
a velocidade de Brancadeneve.
Baseando-se nos gráficos apresentados, durante o intervalo de
tempo T observado, podemos concluir corretamente que
a) a aceleração impressa no início por Encantado foi maior do que a
de Brancadeneve.
b) a velocidade máxima atingida por Brancadeneve foi maior do que
a de Encantado.
c) Encantado foi mais longe que Brancadeneve.
d) Brancadeneve percorreu uma distância maior do que Encantado.
e) a velocidade média de Brancadeneve é menor do que a de
Encantado.
05. (Uern 2013) Seja o gráfico da velocidade em função do tempo de
um corpo em movimento retilíneo uniformemente variado
representado abaixo.
Considerando a posição inicial desse movimento igual a 46 m, então
a posição do corpo no instante t = 8 s é
a) 54 m.
b) 62 m.
c) 66 m.
d) 74 m.
06. (Uern 2013) O gráfico abaixo representa a variação da
velocidade de um móvel em função do tempo.
A distância total percorrida pelo corredor, em metros, durante o
período de tempo em que ele possuía aceleração diferente de zero,
é
a) 4
b) 7
c) 8
d) 14
e) 22
03. (Uerj 2015) Em uma pista de competição, quatro carrinhos
elétricos, numerados de I a IV, são movimentados de acordo com o
gráfico v  t a seguir.
Se o deslocamento efetuado pelo móvel nos 10 s do movimento e
igual a 40 m, então a velocidade inicial v0 e igual a
a) 4 m/s.
b) 5 m/s.
c) 6 m/s.
d) 7 m/s.
07. (G1 - cftmg 2012) Um corpo tem seu movimento representado
pelo gráfico abaixo.
O carrinho que percorreu a maior distância em 4 segundos tem a
seguinte numeração:
e) I – acelerado; II – repouso; III – retrógrado.
11. (Pucpr 2010) Um motociclista dirige uma motocicleta ao longo de
uma estrada reta como mostrado no diagrama velocidade x tempo.
Ao final de duas horas de movimento, seu deslocamento, em km,
será igual a
a) 0.
b) 20.
c) 40.
d) 80.
08. (Espcex (Aman) 2012) O gráfico abaixo representa a
velocidade(v) de uma partícula que se desloca sobre uma reta em
função do tempo(t). O deslocamento da partícula, no intervalo de 0 s
a 8 s foi de:
A respeito dessa situação, assinale a alternativa correta:
a) Entre os instantes t = 3 s e t = 5 s o movimento é acelerado.
b) A aceleração no intervalo de tempo entre t = 5 s e t = 7 s vale – 4
m/s2.
c) O deslocamento do motociclista entre os instantes t = 3 s e t = 5 s
foi de 20 m.
d) A aceleração no intervalo de tempo entre t = 5 s e t = 7 s vale 2
m/s2.
e) A aceleração no intervalo de tempo entre t = 0 e t = 3 s é nula.
12. (G1 - cftsc 2010) O gráfico abaixo representa a variação da
velocidade em função do tempo de uma partícula em movimento
uniformemente variado.
a) – 32m
b) – 16m
c) 0 m
d) 16 m
e) 32 m
09. (Espcex (Aman) 2011) O gráfico abaixo indica a posição (S) em
função do tempo (t) para um automóvel em movimento num trecho
horizontal e retilíneo de uma rodovia.
Da análise do gráfico, pode-se afirmar que o automóvel
a) está em repouso, no instante 1 min.
b) possui velocidade escalar nula, entre os instantes 3 min e 8 min.
c) sofreu deslocamento de 4 km, entre os instantes 0 min e 3 min.
d) descreve movimento progressivo, entre os instantes 1 min e 10
min.
e) tem a sua posição inicial coincidente com a origem da trajetória.
Em relação à área abaixo da reta do gráfico, é correto afirmar que
ela representa a:
a) aceleração média.
b) velocidade média.
c) variação da velocidade.
d) distância percorrida pela partícula.
e) velocidade instantânea.
13. (Ufla 2010) Um móvel se desloca numa trajetória retilínea e seus
diagramas de velocidade e espaço em relação ao tempo são
mostrados a seguir:
10. (G1 - ifsc 2011) O gráfico a seguir apresenta o movimento de um
carro.
O móvel muda o sentido de seu movimento na posição:
a) 10 m
b) 30 m
c) 5 m
d) 20 m
Em relação ao tipo de movimento nos trechos I, II e III, assinale a
alternativa correta.
a) I – acelerado; II – repouso; III – MRUv.
b) I – retardado; II – repouso; III – retrógrado.
c) I – acelerado; II – MRU; III – retrógrado.
d) I – acelerado; II – repouso; III – progressivo.
14. (Unemat 2010) Um corpo possui movimento retilíneo, com
velocidade variando no decorrer do tempo, conforme o gráfico
abaixo.
Assinale a alternativa correta.
a) A aceleração do corpo é nula no intervalo de tempo IV.
b) A aceleração do corpo é constante no intervalo de tempo IV.
c) A aceleração do corpo é nula no intervalo de tempo I.
d) A aceleração do corpo é maior no intervalo de tempo III do que no
intervalo de tempo I.
e) A aceleração do corpo é variável nos intervalos de tempo II e IV.
15. (G1 - cftmg 2010) O gráfico da velocidade em função do tempo
representa o movimento de uma partícula.
Esse movimento pode ser classificado como ____________ no
intervalo de tempo compreendido entre __________.
A opção que completa, corretamente, as lacunas acima é
a) acelerado, zero e 1 h.
b) acelerado, zero e 2 h.
c) desacelerado, zero e 1 h.
d) desacelerado, 1 h e 2 h.
GABARITO:
Resposta da questão 1: [A]
A distância pedida (d) é numericamente igual à soma das áreas dos
dois trapézios, destacados no gráfico.

 2  0,5 1
2  0,5

 1 2  0,5  1,25  2  3,75 m.
DI 
2
2





1,5  1 2  1,5  1  0,5  2,5  1,5  4,5 m.
1 1

DII 
2
2





2 1
 2  1  1  2  3 m.
DIII 
2





D  3  0,5   0,5  11  0,75  0,75  1,5 m.
 IV
2
2
Resposta da questão 4: [D]
 25  5    20  10    10  25  5    20  10   12
d  A1  A2  

2
2
d   20  10   5   20  10   6  150  180 

Tomando como unidade (u) o lado de cada quadrículo, e usando a
propriedade do gráfico da velocidade  tempo, as áreas dos trapézios
fornecem as distâncias percorridas por Encantado (dE) e
Brancadeneve (dB):

5 1
dE  2  4  dE  12 u.

d  6  4  3  d  15 u.
B
 B
2
d  330 m.
Resposta da questão 2: [D]
A distância percorrida nos gráficos de velocidade por tempo é obtida
a partir do cálculo da área sob o mesmo. Para o caso de trechos onde
a aceleração é diferente de zero, correspondem aos trechos em que
a velocidade muda, ou seja, entre 2 e 6 segundos, conforme figura
abaixo.

dB  dE .
Resposta da questão 5: [B]
Dado: S0 = 46 m.
Do gráfico:
Δv 0  10
t  0  v 0  10 m/s
 a

 a  2 m/s2 .

t

5
s

v

0
Δ
t
5

0

Aplicando a função horária do espaço para o instante t = 8 s:
a
2
S  S0  v0 t  t 2  S  46  10  8  
8 2  46  80  64 
2
2
S  62 m.
Resposta da questão 6: [B]
A área do trapézio entre a linha do gráfico e o eixo dos tempos é
numericamente igual ao deslocamento efetuado.
d  A1  A 2
43
d
 4  2  d  6  8  d  14 m
2
40 
10  6
80
v0  v0 
2
16

v 0  5 m/s.
Resposta da questão 7: [A]
Resposta da questão 3: [B]
No gráfico v  t, a distância percorrida é obtida pela ”área" entre a
linha do gráfico e o eixo dos tempos. Calculando cada uma delas:
No gráfico da velocidade em função do tempo, a “área” (A) entre a
linha do gráfico e o eixo t dá o deslocamento escalar.
1 40  1 40 
ΔS  ΔS01  ΔS12 

 20  20 
2
2
ΔS  0.
Resposta da questão 8: [C]
As áreas da figura abaixo representam o deslocamento. Como uma
é positiva e a outra negativa de mesmo módulo, o deslocamento total
é nulo.
S = S – S0  10 = S – 20  S = 30 m.
Resposta da questão 14: [B]
Como o movimento é retilíneo, a aceleração tem módulo igual ao
módulo da aceleração escalar, dado por:
| a |
| v |
. Assim:
t
aI = aII (constante)  0; aIII = 0; aIV  0 (constante)
Resposta da questão 9: [B]
Note que entre 3 e 8 min a posição não varia. Portanto, o carro está
parado.
Resposta da questão 10: [E]
No trecho I, a declividade da curva espaço-tempo está aumentando,
portanto o módulo da velocidade está aumentando, logo o
movimento é acelerado.
No trecho II, o espaço é constante, portanto o móvel está em
repouso.
No trecho III, o espaço diminui linearmente com o tempo, tratandose de um movimento uniforme retrógrado.
Resposta da questão 11:[B]
Analisemos cada intervalo:
– De 0 a 3 s: o movimento é uniformemente acelerado; a aceleração
escalar é
a1 =
v1 8
  2,7 m/s2.
t1 3
O espaço percorrido é calculado pela “área” de 0 a 3 s
S1 
38
 12 m.
2
– De 3 s a 5 s: o movimento é uniforme, com velocidade escalar v2 =
8 m/s.
O espaço percorrido é:
S2 = v2 t2  8  2 = 16 m.
– De 5 s s 7 s: o movimento é uniformemente retardado; a aceleração
escalar é:
a3 =
v 3 0  8 8


 4 m/s2.
t3 7  5 2
O espaço percorrido é:
S3 
28
 8 m.
2
Resposta da questão 12: [D]
Propriedade do gráfico v  f(t) : a área entre a linha do gráfico e o
eixo t representa o espaço percorrido pelo móvel ( S). Como não
há mudança de sentido, o espaço percorrido é igual à distância
percorrida.
Resposta da questão 13: [B]
Como o gráfico da velocidade em função do tempo é uma reta, tratase de movimento uniformemente variado. Desses gráficos podemos
tirar que:
S0 = 0; v0 = 10 m/s.
Podemos ainda concluir que no instante t = 2 s a velocidade se anula
(v = 0), ou seja, o móvel inverte o sentido de seu movimento, uma
vez que a trajetória é retilínea.
Calculando o espaço percorrido de 0 a 2 s pela “área” no primeiro
gráfico:
S =
Mas:
2  10
 10 m.
2
Resposta da questão 15: [C]
No intervalo de 0 a 1 h, a velocidade escalar é positiva e tem módulo
decrescente. Então, o movimento é progressivo e desacelerado.
No intervalo de 1 h a 2 h, a velocidade escalar é negativa e tem
módulo crescente. Então, o movimento é regressivo (ou retrógrado)
e acelerado.