Gráficos de MUV – Velocidade pelo tempo

Gráficos de M.U.V. – Movimento Uniformemente Variado
Velocidade pelo Tempo
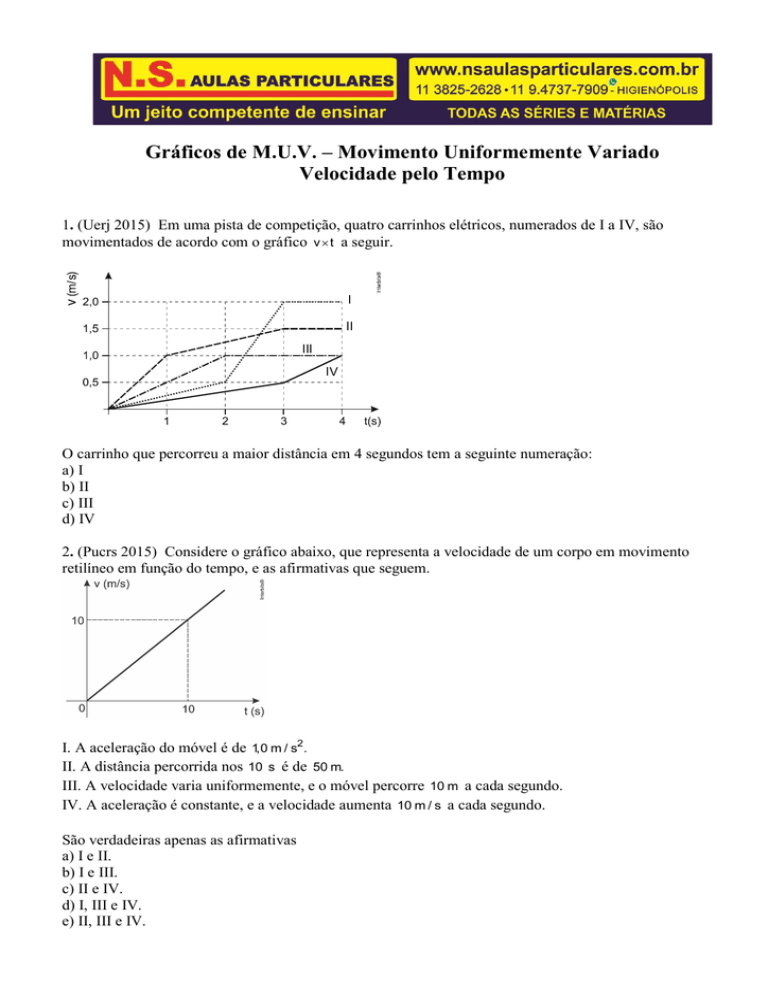
1. (Uerj 2015) Em uma pista de competição, quatro carrinhos elétricos, numerados de I a IV, são
movimentados de acordo com o gráfico v  t a seguir.
O carrinho que percorreu a maior distância em 4 segundos tem a seguinte numeração:
a) I
b) II
c) III
d) IV
2. (Pucrs 2015) Considere o gráfico abaixo, que representa a velocidade de um corpo em movimento
retilíneo em função do tempo, e as afirmativas que seguem.
I. A aceleração do móvel é de 1,0 m / s2.
II. A distância percorrida nos 10 s é de 50 m.
III. A velocidade varia uniformemente, e o móvel percorre 10 m a cada segundo.
IV. A aceleração é constante, e a velocidade aumenta 10 m / s a cada segundo.
São verdadeiras apenas as afirmativas
a) I e II.
b) I e III.
c) II e IV.
d) I, III e IV.
e) II, III e IV.
3. (Uern 2015) O gráfico representa a variação da velocidade de um automóvel ao frear.
Se nos 4 s da frenagem o automóvel deslocou 40m, então a velocidade em que se encontrava no instante em
que começou a desacelerar era de
a) 72km / h.
b) 80km / h.
c) 90km / h.
d) 108km / h.
4. (Ufpr 2015) Um veículo está se movendo ao longo de uma estrada plana e retilínea. Sua velocidade em
função do tempo, para um trecho do percurso, foi registrada e está mostrada no gráfico abaixo. Considerando
que em t  0 a posição do veículo s é igual a zero, assinale a alternativa correta para a sua posição ao final
dos 45s.
a)
b)
c)
d)
e)
330m.
480m.
700m.
715m.
804m.
5. (Imed 2015) Considere um carro que se movimenta ao longo de uma pista retilínea. O gráfico abaixo
descreve a velocidade do carro em função do tempo, segundo um observador em repouso sobre a calçada.
Em relação a essa situação, assinale a alternativa correta.
a) O movimento é uniformemente variado.
b) O carro realiza um movimento retilíneo uniforme.
c) Ao final do movimento (t  8s), o carro retorna à sua posição de
origem (t  0).
d) O carro está freando no intervalo 4s  t  8s.
e) Em t  4, o carro inverte o sentido do seu movimento.
6. (Unesp 2014) Um motorista dirigia por uma estrada plana e retilínea quando, por causa de obras, foi
obrigado a desacelerar seu veículo, reduzindo sua velocidade de 90 km/h (25 m/s) para 54 km/h (15 m/s).
Depois de passado o trecho em obras, retornou à velocidade inicial de 90 km/h. O gráfico representa como
variou a velocidade escalar do veículo em função do tempo, enquanto ele passou por esse trecho da rodovia.
Caso não tivesse reduzido a velocidade devido às obras, mas mantido sua velocidade constante de 90 km/h
durante os 80 s representados no gráfico, a distância adicional que teria percorrido nessa estrada seria, em
metros, de
a) 1 650.
b) 800.
c) 950.
d) 1 250.
e) 350.
7. (Uerj 2014) O gráfico abaixo representa a variação da velocidade dos carros A e B que se deslocam em
uma estrada.
Determine as distâncias percorridas pelos carros A e B durante os primeiros cinco segundos do percurso.
Calcule, também, a aceleração do carro A nos dois primeiros segundos.
8. (G1 - ifsp 2014) Com a intenção de se preparar para uma maratona, Brancadeneve e Encantado
começaram um treino diário de corrida e pediram ajuda para a experiente maratonista Fadamadrinha. A
instrutora, então, com a ajuda de um dispositivo eletrônico de última geração conhecido como radar, plotou
gráficos da velocidade de cada um pelo tempo em que ficava observando.
Certo dia, apresentou os gráficos aos dois, utilizando para isso a mesma escala nos eixos, sendo VE a
velocidade de Encantado e VB a velocidade de Brancadeneve.
Baseando-se nos gráficos apresentados, durante o intervalo de tempo T observado, podemos concluir
corretamente que
a) a aceleração impressa no início por Encantado foi maior do que a de Brancadeneve.
b) a velocidade máxima atingida por Brancadeneve foi maior do que a de Encantado.
c) Encantado foi mais longe que Brancadeneve.
d) Brancadeneve percorreu uma distância maior do que Encantado.
e) a velocidade média de Brancadeneve é menor do que a de Encantado.
9. (Uern 2013) Seja o gráfico da velocidade em função do tempo de um corpo em movimento retilíneo
uniformemente variado representado abaixo.
Considerando a posição inicial desse movimento igual a 46 m, então a posição do corpo no instante t = 8 s é
a) 54 m.
b) 62 m.
c) 66 m.
d) 74 m.
10. (Uem 2013) Analise as alternativas abaixo e assinale o que for correto.
01) O gráfico da velocidade em função do tempo, para um móvel descrevendo um Movimento Retilíneo e
Uniforme, é uma reta paralela ao eixo dos tempos.
02) O gráfico da posição em função do tempo, para um móvel descrevendo um movimento Retilíneo e
Uniforme, é uma reta, e o coeficiente angular dessa reta fornece a velocidade do móvel.
04) O gráfico do espaço percorrido em função do tempo é uma reta para um móvel que realiza um
Movimento Uniforme qualquer.
08) O espaço percorrido por um móvel, em um dado intervalo de tempo, pode ser obtido calculando-se a
“área sob a curva” do gráfico da velocidade em função do tempo, para aquele dado intervalo de tempo.
16) O gráfico da velocidade em função do tempo, para um móvel descrevendo um Movimento Retilíneo
Uniformemente Variado, é uma parábola.
11. (Unesp 2013) Dois automóveis estão parados em um semáforo para pedestres localizado em uma rua
plana e retilínea. Considere o eixo x paralelo à rua e orientado para direita, que os pontos A e B da figura
representam esses automóveis e que as coordenadas x A(0) = 0 e xB(0) = 3, em metros, indicam as posições
iniciais dos automóveis.
Os carros partem simultaneamente em sentidos opostos e suas velocidades escalares variam em função do
tempo, conforme representado no gráfico.
Considerando que os automóveis se mantenham em trajetórias retilíneas e paralelas, calcule o módulo do
deslocamento sofrido pelo carro A entre os instantes 0 e 15 s e o instante t, em segundos, em que a diferença
entre as coordenadas xA e xB, dos pontos A e B, será igual a 332 m.
Gabarito:
Resposta da questão 1:
[B]
No gráfico v  t, a distância percorrida é obtida pela ”área" entre a linha do gráfico e o eixo dos tempos.
Calculando cada uma delas:

 2  0,5 1
2  0,5

 1 2  0,5  1,25  2  3,75 m.
DI 
2
2





1,5  1 2
1 1

 1,5  1  0,5  2,5  1,5  4,5 m.
DII 
2
2





2 1
 2  1  1  2  3 m.
DIII 
2





D  3  0,5   0,5  11  0,75  0,75  1,5 m.
 IV
2
2
Resposta da questão 2:
[A]
[I] Verdadeira. Aplicando a definição de aceleração escalar média:
a  am 
Δv 10

 a  1 m/s2.
Δt 10
[II] Verdadeira. O espaço percorrido é dado pela área entre a linha do gráfico e o eixo dos tempos.
ΔS 
10  10
 ΔS  50 m.
2
[III] Falsa. A velocidade é variável.
[IV] Falsa. A velocidade aumenta 1,0 m/s a cada segundo.
Resposta da questão 3:
[A]
Utilizando os dados fornecidos no enunciado, temos que:
ΔS  v o  t 
a  t2
2
Onde,
a
ΔV v  vo vo


Δt
4
4
Logo,
 v o  2
 4 4

40  v o  4  
2
40  4  v o  2  v o
v o  20 m s ou v o  72 km h
Resposta da questão 4:
[D]
Como a posição inicial é zero, a sua posição final será exatamente igual à distância percorrida. Sabendo que a
distância percorrida é igual numericamente à área do gráfico, então:
ΔST  A1  A2  A3  A4  A5
Porém, para que seja possível calcular as áreas 4 e 5, é necessário encontrar o tempo em que acontece a
mudança de sentido na velocidade (ponto em que cruza o eixo x).
Sabendo que o movimento de 1 para 2 é um Movimento Retilíneo Uniformemente Variado (MRUV),
podemos analisar este intervalo de tempo para encontrar a aceleração.
v  v 0  at
10  36  a  5
a  9,2 m s
Agora, analisando o trecho de 1 para 3, temos que:
v  v 0  at
0  36  9,2  t
t 3,9 s
Assim,
 15  5   28   10  28   3,9  36    6,1  5   10 
ΔST   35  8   




2
2

  2   2  

ΔST  280  280  140  70,2  55,5
ΔST  714,7 m
ΔST
715 m
Resposta da questão 5:
[D]
Analisando as alternativas,
[A] INCORRETA. Em um movimento uniformemente variado, a aceleração é constante durante o
movimento. O Gráfico mostra claramente que na primeira parte do movimento o módulo da velocidade
está aumentando (aceleração maior que zero) e na segunda parte diminuindo (aceleração menor que zero).
Desta forma, pode-se dizer que a aceleração não é constante durante o movimento.
[B] INCORRETA. Um movimento retilíneo uniforme tem aceleração nula.
[C] INCORRETA. Em momento algum do movimento descrito na figura existe uma inversão de sentido do
movimento. Logo, o carro não irá retornar a sua posição inicial.
[D] CORRETA.
[E] INCORRETA. Inverte o sentido de sua aceleração e não do movimento (velocidade).
Resposta da questão 6:
[E]
A distância (D) pedida é numericamente igual à área hachurada no gráfico.
D
50  20
 10  D  350 m.
2
Resposta da questão 7:
 Distâncias percorridas pelos carros:
No gráfico v  t a distância percorrida é numericamente igual à área entre a linha do gráfico e o eixo dos
tempos. Assim:
53

DA  2  2  DA  8 m.


D   4  1  2    3  1  D  8 m.
A
B
 2




 Aceleração do carro A:
Dados: v0 = 0; v = 2 m/s; Δt  2s.
Entendendo por aceleração apenas a aceleração escalar do veículo, temos:
a
Δv 2  0

 a  1 m/s2 .
Δt
2
Resposta da questão 8:
[D]
Tomando como unidade (u) o lado de cada quadrículo, e usando a propriedade do gráfico da velocidade 
tempo, as áreas dos trapézios fornecem as distâncias percorridas por Encantado (dE) e Brancadeneve (dB):

5 1
dE  2  4  dE  12 u.

d  6  4  3  d  15 u.
B
 B
2

dB  dE.
Resposta da questão 9:
[B]
Dado: S0 = 46 m.
Do gráfico:
t  0  v 0  10 m/s



t  5 s  v  0
 a
Δv 0  10

 a  2 m/s2 .
Δt
50
Aplicando a função horária do espaço para o instante t = 8 s:
S  S0  v 0 t 
a 2
2
t  S  46  10  8  
8 2  46  80  64 
2
2
S  62 m.
Resposta da questão 10:
01 + 02 + 04 + 08 = 15.
[01] Correta.
A velocidade não varia com o tempo, tratando-se de uma função constante, assim, o gráfico uma reta
paralela ao eixo dos tempos.
[02] Correta.
A função horária da posição em função do tempo para o Movimento Uniforme é S  S0  vt. Tratando-se
de uma função do 1º grau, o gráfico é uma reta cujo coeficiente angular é  ΔS Δt  v .
[04] Correta.
A função horária do espaço percorrido em função do tempo para o Movimento Uniforme é ΔS  vt.
Tratando-se de uma função do 1º grau, o gráfico é uma reta.
[08] Correta.
No gráfico v  t, a “área” entre a linha do gráfico e o eixo dos tempos dá o espaço percorrido.
[16] Incorreta.
No Movimento Uniformemente Variado, a função horária da velocidade é v  v0  at. Como é uma função do
1º grau, o gráfico da velocidade em função do tempo é uma reta.
Resposta da questão 11:
Calculando o deslocamento  Δx A  do móvel A até o instante t = 15 s.
Da propriedade do gráfico v  t.
x A  "área" 
15  10
 10  x A  25  5 
2
x A  125 m.
Calculando o instante em que a distância entre os móveis é igual a 332 m, usando novamente a propriedade
anterior:
Δx A 
t   t  5
2
 10   2 t  5  5
 Δx A  10 t  25.
Sendo x0A  0, temos:
x A  x0A  Δx A  0  10 t  25  x A  10 t  25 .
 t   t  8 
ΔxB   
  10    2 t  8  5
2


 ΔxB  10 t  40.
Sendo x0B  3 m, temos:
xB  x0B  Δx A  3  10 t  40  xB  10 t  43.
No instante t a distância entre os móveis DAB  deve ser 332 m.
DAB  x A  xB  332  10 t  25   10 t  43   332  20 t  68  20 t  400
t  20 s.
