1. (2,0 pontos) Transforme os números para a base 2: a. 1345,125

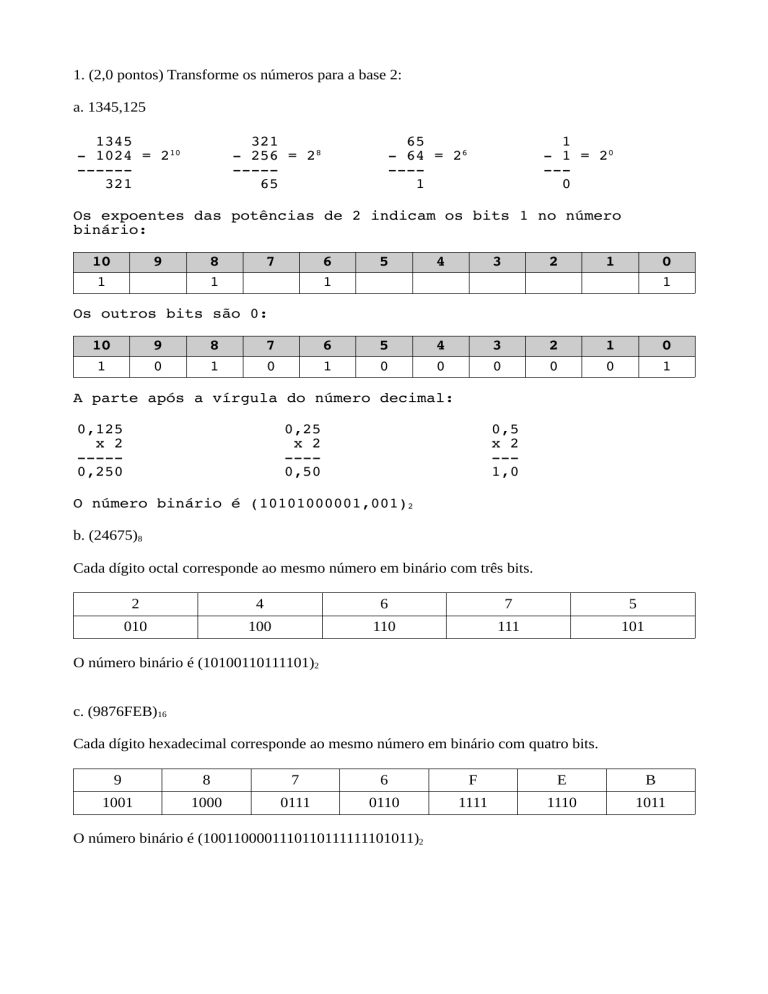
1. (2,0 pontos) Transforme os números para a base 2:
a. 1345,125
1345
- 1024 = 210
-----321
321
- 256 = 28
----65
65
- 64 = 26
---1
1
- 1 = 20
--0
Os expoentes das potências de 2 indicam os bits 1 no número
binário:
10
1
9
8
1
7
6
1
5
4
3
2
1
0
1
6
1
5
0
4
0
3
0
2
0
1
0
0
1
Os outros bits são 0:
10
1
9
0
8
1
7
0
A parte após a vírgula do número decimal:
0,125
x 2
----0,250
0,25
x 2
---0,50
0,5
x 2
--1,0
O número binário é (10101000001,001)2
b. (24675)8
Cada dígito octal corresponde ao mesmo número em binário com três bits.
2
4
6
7
5
010
100
110
111
101
O número binário é (10100110111101)2
c. (9876FEB)16
Cada dígito hexadecimal corresponde ao mesmo número em binário com quatro bits.
9
8
7
6
F
E
B
1001
1000
0111
0110
1111
1110
1011
O número binário é (1001100001110110111111101011)2
2. (2,0 pontos) Transforme os números para a base 8:
a. (1011010100111)2
Cada três bits do menos significativo ao mais significativo (da direita para a esquerda) corresponde
a um dígito octal.
1
011
010
100
111
1
3
2
4
7
O número em octal é (13247)8
b. 1371
1371
- 1368
---3
/ 8
171
- 168
--3
/ 8
21
- 16
-5
/ 8
2
- 0
2
/ 8
0
O número em octal é (2533)8
c. (910ABC473)16
A maneira mais rápida de realizar a transformação de um número hexadecimal para octal é primeiro
passá-lo para binário e depois para octal. Cada dígito hexadecimal correspondem ao mesmo número
em binário com quatro bits.
9
1
0
A
B
C
4
7
3
1001
0001
0000
1010
1011
1100
0100
0111
0011
Agora, basta considerar do bit menos significativo ao mais significativo (da direita para a esquerda),
cada três bits correspondem ao mesmo número em octal.
100
100
010
000
101
010
111
100
010
001
110
011
4
4
2
0
5
2
7
4
2
1
6
3
O número em octal é (442052742163)8
3. (2,0 pontos) Transforme os números para a base 10:
a. (1001110,111)2
6
5
4
3
2
1
0
1
0
0
1
1
1
0
3
2
1
,
-1
-2
-3
1
1
1
2
6
-1
-2
0
0
2
2
2
0
,
2
2
2-3
64
0
0
8
4
2
0
,
0,5
0,25
0,125
64 + 8 + 4 + 2 + 0,5 + 0,25 + 0,125 = 78,875
O número decimal é 78,875
b. (3241)8
3
2
1
0
3
2
4
1
3 * 83
2 * 82
4 * 81
1 * 80
3 * 512
2 * 64
4*8
1*1
1536
128
32
1
1536 + 128 + 32 + 1 = 1697
O número decimal é 1697
c. (CEF)16
2
1
C
0
E
F
12 * 16
2
14 * 16
15 * 160
12 * 256
14 * 16
15 * 1
3072
224
15
3072 + 224 + 15 = 3311
O número decimal é 3311
1
4. (2,0 pontos) Transforme os números para a base 16:
a. (1111010111110)2
A partir do bit menos significativo cada quatro bits correspondem a um dígito hexadecimal.
1
1110
1011
1110
1
E
B
E
O número em hexadecimal é (1EBE) 16
b. 1231
1231
- 1216
-----15
/
16
76
- 64
---12
12 = (C)16
/ 16
4
- 0
--4
/ 16
0
15 = (F)16
O número hexadecimal é (4CF)16
c. (7531)8
A maneira mais rápida de realizar esta transformação é passando o número inicialmente para binário
e depois para hexadecimal.
7
5
3
1
111
101
011
001
1111
0101
1001
F
5
9
O número hexadecimal é (F59)16
5. (2,0 pontos) Realize as operações sem transformar os números de base. Se o número binário for
negativo, considere o complemento de 2 do mesmo.
a. (1001)2 - (100111)2
O complemento de 2 do subtraendo deve ser calculado:
100111
||||||
011000 -> Complemento de 1
+ 1
------011001 -> Complemento de 2
Este complemento de 2 será somado com o minuendo com a mesma
quantidade de bits:
11 1
001001
+ 011001
-------100010 -> Resultado da subtração em binário
b. (3456)8 + (7654)8
1111
3456
+ 7654
-----13332 -> Resultado da soma em octal
c. (ABDE8)16 + (76A459)16
11111
ABDE8
+ 76A459
-------816241 -> Resultado da soma em hexadecimal
d. (101011)2 + (10101)2
111111
101011
+ 10101
-------1000000 -> Resultado da soma em binário
e. (1001)2 * (110)2
1001
* 110
-----0000
1001
+ 1001
-------110110 -> Resultado da multiplicação em binário
f. (100101)2 / (1101)2
100101
- 1101
-------001011
/ 1101
10
Quociente = (10)2
Resto = (1011)2