2 - Portal IFSC SJ

Instituto Federal de Santa Catarina
Campus São José
Área de Telecomunicações
Curso Técnico Integrado em Telecomunicações
Eletrônica Digital
Sistema de Numeração
INTRODUÇÃO
• Eletrônica digital trabalha com sinais discretos;
• Usa os mesmos componentes da eletrônica analógica – resistores,
capacitores, diodos, transistores, etc;
• Sinal analógico: contínuo no tempo;
• Sinal digital: discreto no tempo – existe uma descontinuidade entre
uma condição e outra;
• Exemplo: termômetro.
Grandeza
Grandeza
Analógico vs Digital
Sinal analógico ou contínuo
Sinal Discreto
Grandeza
Tempo
Tempo
Sinal Digital
Tempo
Sistema de Numeração
• Origem dos números surgiu da necessidade de contar;
• Dizem que surgiu há mais de 3500 anos. O Teorema de Pitágoras data
de 500 anos A.C., para se ter uma ideia;
• O sistema de numeração normalmente utilizado é o DECIMAL, com
números entre 0 e 9;
• Descrição geral de um número em qualquer base:
Y
...+ X.Base +...
• X → dígito do número em questão;
• Base → é a base do sistema de numeração.
Sistema de Numeração
• Y → posição do dígito em relação a vírgura. Positivo à esquerda e
negativo à direita (os números decimais);
• Y → vale 0 para o 1º dígito à direita da vírgula, 1 para o 2º dígito e
assim por diante;
• Y → vale -1 para o 1º dígito à esquerda da vírgula, -1 para o 2º dígito
e assim por diante;
• Os dígitos sempre iniciam em zero;
• Para um sistema de numeração com base N, os dígitos vão de 0 até
N-1;
• Quando se atinge a contagem N, um novo dígito é acrescentado à
direita do número (parte inteira), por exemplo: 9 para 10.
Exemplos
3
2
1
0
-1
-2
• (1.036,87)10 = 1 x 10 + 0 x 10 + 3 x 10 + 6 x 10 + 8 x 10 + 7 x 10 =
1000 + 0 + 30 + 6 + 0,80 + 0,07 = 1036,8710
0
-1
-2
-3
• (0,013)10 = 0 x 10 + 0 x 10 + 1 x 10 + 3 x 10 = 0,010 + 0,003 =
0,01310
5
4
2
1
0
• (230.941)10 = 2 x 10 + 3 x 10 + 9 x 10 + 4 x 10 + 1 x 10 = 200000 +
30000 + 900 + 40 + 1 = 23094110
Exercícios
• Represente os números decimais na forma:
• (13)10;
• (0,13)10;
• (128)10;
• (2.049,05)10;
• (935.089)10;
• (1.000.001,009)10;
• (0,00001)10;
X.Base
Y
Sistema Binário
• Base é 2;
• O dígitos que formam este sistema de numeração são: 0 e 1;
• Amplamente utilizado em projetos de circuitos eletrônicos. Por
exemplo, o bit 0 pode representar uma tensão de -5V e o bit 1 uma
tensão de +5V;
• Conversão de número binário para decimal:
5
4
3
2
1
0
• (110101)2 = 1 x 2 + 1 x 2 + 0 x 2 + 1 x 2 + 0 x 2 + 1 x 2 =
= (1 x 32) + (1 x 16) + (0 x 8) + (1 x 4) + (0 x 2) + (1 x 1) =
= 32 + 16 + 4 + 1 = (53)10
• Sempre que o dígito mais a direita for 1, então, o número será
sempre ímpar! Por quê?
Sistema Binário
• Outros exemplos:
3
2
1
0
• (1110)2 = 1 x 2 + 1 x 2 + 1 x 2 + 0 x 2 =
= (1 x 8) + (1 x 4) + (1 x 2) + (0 x 1) =
= 8 + 4 + 2 = (14)10
5
4
3
2
1
0
• (001110)2 = 0 x 2 + 0 x 2 + 1 x 2 + 1 x 2 + 1 x 2 + 0 x 2 =
= (0 x 32) + (0 x 16) + (1 x 8) + (1 x 4) + (1 x 2) + (0 x 1) =
= 8 + 4 + 2 = (14)10
5
4
3
2
1
0
• (111000)2 = 1 x 2 + 1 x 2 + 1 x 2 + 0 x 2 + 0 x 2 + 0 x 2 =
= (1 x 32) + (1 x 16) + (1 x 8) + (0 x 4) + (0 x 2) + (0 x 1) =
= 32 + 16 + 8 = (56)10
Sistema Binário
• Conversão de decimal para binário:
• (14)10: 14 2
0 7
1
• (17)10:
2
3
2
1
1
1410 = 11102
17 2
1
8
0
2
4
0
1710 = 100012
2
2
0
2
1
Exercícios
• Converta os números abaixo do sistema binário para o decimal:
• (100)2:
• (101)2:
• (1000)2:
• (111001)2:
• (00111)2:
• (0101)2:
• (101010)2:
• (1111111111)2:
Exercícios
• Converta os números abaixo do sistema decimal para o binário:
• (100)10:
• (17)10:
• (63)10:
• (32)10:
• (8)10:
• (79)10:
• (21)10:
• (127)10:
Sistema Binário
• Conversão da parte fracionário do nº decimal para binário:
• Multiplica-se a parte fracionária pelo valor da base;
• O número resultante à esquerda da vírgula é o dígito (0 ou 1)
procurado;
• Se o dígito à esquerda for 0 (zero) continuar multiplicando pela base;
• Se o dígito à esquerda for 1 (um), retira-se o 1 e prossegue a
multiplicação;
• O processo continua até obter-se 0 (zero) como resultado, ou atingir
a resolução estabelecida, no caso de dízima (nº de casas após a
vírgula);
• A leitura dos dígitos é feita de cima para baixo, ao contrário da parte
inteira.
Exemplos
• (0,625)10:
0,625
x 2
1,250
0,250
x 2
0,50
0,50
x 2
1,00
(0,101)2
Exemplos
• (0,27)10:
0,27
x 2
0,54
0,54
x 2
1,08
0,08
x 2
0,16
0,16
x 2
0,32
0,32
x 2
0,64
0,64
x 2
1,28
(0,010001)2
Exercícios
• Faça a conversão dos seguintes números decimais para binário, com
até cinco casas decimais após a vírgula:
• (0,32)10:
• (0,66)10:
• (1,20)10:
• (13,48)10:
• (230,01)10:
• (1010,10)10:
• (8036,85)10:
Sistema Octal
• A base do sistema de numeração é igual o número de dígitos que ela
usa. No sistema octal a base é 8, portanto tem 8 dígitos:
0, 1, 2, 3, 4, 5, 6 e 7 (0 até N-1, N → base do sistema de numeração)
• Sua utilidade nos sistemas digitais vem do fato de que, associando-se
os algarismos de um número binário (bits) em grupos de três, obtémse uma corresnpondência direta com os dígitos do sistema octal.
23 = 810 (2 → sistema binário; 3 → quantidade de bits)
• Conversão de octal para decimal:
Sistema Octal
• 1247,2358 = ?10
= 1 x 83 + 2 x 82 + 4 x 81 + 7 x 80 + 2 x 8-1 + 3 x 8-2 + 5 x 8-3 =
= 1 x (23)3 + 2 x (23)2 + 4 x (23)1 + 7 x (23)0 + 2 x (23)-1 + 3 x (23)-2 +
+ 5 x (23)-3 =
= 1 x 29 + 2 x 26 + 4 x 23 + 7 x 20 + 2 x 2-3 + 3 x 2-6 + 5 x 2-9 =
= 1 x 512 + 2 x 64 + 4 x 8 + 7 x 1 + 2 x (1/8) + 3 x (1/64) + 5 x (1/512) =
= 512 + 128 + 32 + 7 + 0,125 + 0,046875 + 0,009765625 =
= 679,18164062510
= 679,18164110
Sistema Octal
• Conversão de decimal para octal:
• 22310 = ?8
223 8
7 27
3
8
3
= 3378
• Converter o número fracionário 380,796 da base decimal para octal,
com 4 casas decimais após a vírgula:
• 380,79610 = 38010 + 0,79610
• Primeiro converte-se a parte inteira, depois a fracionária.
Sistema Octal
• Parte inteira:
Parte fracionária:
380 8
4 47
7
8
5
= 5748
0,796
x 8
6,368
0,368
x 8
2,944
0,944
x 8
7,952
0,952
x 8
4,416
= 0,62748
Para → 4 casas após a vírgula!
• 380,79610 = 574,62748
Sistema Octal
• Conversão de octal em binário:
• O mais intuitivo é converter primeiro para a base decimal e depois
para a base binária. Mas como a base octal é 23, ou seja, terceira
potência de 2, existe uma correspondência direta entre as bases.
OCTAL
BINÁRIO
0
000
1
2
001
010
3
4
011
100
5
6
7
101
110
111
Sistema Octal
• Por exemplo:
001
175,4328
010
011
111
101
100
• 175,4328 = ( 001 111 101 , 100 011 010 )2
• Reescrevendo: 1111101,100011012
• Agrupa-se os valores binários sempre de 3 em 3 bits. Adicionando-se
zeros à esquerda na parte inteira, e à direita na parte fracionária,
quando necessário.
Sistema Octal
• Conversão de binário para octal:
• Agrupa-se os bits de 3 em 3 a partir da vírgula, para a direita e para a
esquerda:
• 10111011001,00011012 =
= 010 111 011 001 , 000 110 100
= 2
7
3
1 , 0
6
4
= 2731,0648
• 1011101,11112 = 001 011 101 , 111 100
= 1
3
5 , 7
4 = 135,748
Sistema Octal
• Converta o número 123810 para binário:
• 1ª alternativa: dividir 123810 sucessivamente por 2. Mas é uma
solução bastante extensa!
• 2ª alternativa: converter 123810 para octal e, em seguida, converter
para binário. Solução menos trabalhosa, veja!
• 123810
1238 8
6 154 8
2 19 8
3 2
= 23268
• Agora converte-se 23268 para binário:
Sistema Octal
• 23268 = (010 011 010 110)2 = 100110101102
• Exercícios:
• Resolva as conversões numéricas propostas a seguir:
– (24)10 = (?)8 = (?)2
– (132)10 = (?)8 = (?)2
– (98)10 = (?)8 = (?)2
– (556)10 = (?)8 = (?)2
– (1024)10 = (?)8 = (?)2
– (100)10 = (?)8 = (?)2
Sistema Hexadecimal
• Este sistema apresenta a base 16, portanto possui 16 dígitos
distintos. Os valores usados são:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
• Nomenclatura mais usadas na base hexadecimal:
– 53A,E216
– 0x53A,E2
• O sistema hexadecimal também apresenta equivalência direta entre
seus dígitos e grupos de 4 dígitos binários:
Sistema Hexadecimal
HEXADECIMAL
BINÁRIO
0
1
0000
0001
2
3
0010
0011
4
5
6
0100
0101
0110
7
0111
8
1000
9
1001
A
1010
B
1011
C
1100
D
1101
E
1110
F
1111
Sistema Hexadecimal
• Conversão de decimal para hexadecimal:
• 637,3310 = ?16
637 16
13 39 16
7 2
= 27D16 = 0x27D
• 637,3310 = 27D,547A16
0,33
x 16
5,28
0,28
x 16
4,48
0,48
x 16
7,68
0,68
x 16
10,88
= 0,547A16
Sistema Hexadecimal
• Conversão de hexadecimal para decimal:
• AFC0,7D16 = ?10
= A x 163 + F x 162 + C x 161 + 0 x 160 + 7 x 16-1 + D x 16-2 =
= 10 x 163 + 15 x 162 + 12 x 161 + 0 x 160 + 7 x 16-1 + 13 x 16-2 =
= 44992,4882810
• Conversão de hexadecimal para binário:
• FAFA,CACA16 = ?2
=
F
A
F
A ,
C
A
C
A
= 1111 1010 1111 1010 , 1100 1010 1100 1010
= 1111101011111010,11001010110010102
Sistema Hexadecimal
• Conversão de binário para hexadecimal:
• 1011101010111010,0011111012 = ?16
= 1011 1010 1011 1010 , 0011 1110 1000
= B
A
B
A , 3
E
8
= BABA,3E816
• Tabela de conversão de sistemas de numeração:
Tabela de conversões
DE/PARA
2
8
10
16
2
8
10
16
Operações Numéricas
• Adição e subtração no sistema decimal:
• Adição:
Vai um - Transporte - “ Carry”
1111
6489
+ 4768
11257
Obs.: Toda vez que a soma
de dígitos for maior ou igual
ao valor da base (10) oc orre
um vai um.
Operações Numéricas
• Subtração:
Empresta um - Vem um - “ Borrow”
11 1
8123
- 678
7445
Operações Numéricas
• Adição e Subtração no Sistema Binário:
• Como serão os procedimentos que realizarão as operações de soma e
subtração em circuitos digitais?
• Primeiro veremos como representar números positivos e negativos
através de sequências de bits em um tamanho definido pelo HW.
• Para números fracionários o número de bits da sequência deve ser
considerada para a parte fracionária da mesma forma que a parte
inteira.
Operações Numéricas
• Representação de números binários sinalizados:
• A subtração de números binários A e B, A – B, é calculado como a
soma entre o número A e o negativo do número B (– B). Logo,
devemos calcular o negativo do segundo número.
• Para representar números binários negativos serão utilizadas 3
representações:
– Sinal-Magnitude;
– Complemento de 1;
– Complemento de 2.
Operações Numéricas
• Sinal – Magnitude:
• O bit mais significativo, ou seja, o bit mais à esquerda é utilizado para
o sinal.
• 0 → para número positivo
• 1 → para número negativo
• Os demais bits contém o valor da magnitude. Assim um número com
8 bits, possui apenas 7 bits representando a magnitude.
• 0000 11012 = + 1310
• 1000 11012 = – 1310
Operações Numéricas
• Sinal – Magnitude:
• Sendo o formato de 8 bits, é possível representar 28 = 256 números
válidos. No entanto, existem 255 números diferentes nesta
representação. Pois:
• + 010 = 0000 00002
• – 010 = 1000 00002
• Assim os números se estendem no intervalo de -127 até +127.
Operações Numéricas
• Complemento de um:
• O complemento de 1 de um número binário é obtido trocando todos
os zeros por um e os uns por zeros.
• Os números, +13 e -13 decimal, em formato de 8 bits serão:
• 0000 11012 = + 1310
• 1111 00102 = – 1310
• O bit mais significativo (mais à esquerda) representa o sinal. Assim:
• 0 → número positivo
• 1 → número negativo
Operações Numéricas
• Complemento de um:
• Neste caso também teremos o zero positivo (0000 00002) e o zero
negativo (1111 11112).
• E os números se estendem dentro do intervalo de -127 até +127.
• Complemento de dois:
• O complemento de 2 de um número binário é obtido calculando
primeiro o complemento de 1 do número e depois somando 1.
• Por exemplo:
Operações Numéricas
• Os números, +13 e -13 decimal, em formato de 8 bits serão:
• 0000 11012 = + 1310
• 1111 00102 = – 1310 (complemento de 1)
• 1111 00102 + 0000 00012 = 1111 00112
• 1111 00112 = – 1310 (complemento de 2)
• O bit mais significativo do número também é 1 quando o número for
negativo, e 0 quando o número for positivo.
• No formato de 8 bits, agora é possível representar os 256 números
válidos, pois, +0 (0000 00002) e –0 (0000 00002) possuem a mesma
representação binária. COMPROVE!
Operações Numéricas
Operações Numéricas
• Para realizar a subtração entre dois números, é necessário calcular o
complemento de 2 do subtraendo e somar com o minuendo. Isto
resulta em economia de HW e redução de sua complexidade.
• O bit mais significativo vai indicar se o resultado desta subtração
ainda é um número negativo. Você pode saber sua magnitude se fizer
o processo inverso, ou seja, debitar de 1 o resultado e complementar
todos os bits, ou melhor ainda, realizar o complemento 2 sobre este
número.
• Ou seja, complementar 2 vezes é retornar ao número original em
magnitude com sinal positivo. Se o resultado da soma (seja ela entre
números positivos ou negativos) extrapolar o número da seqüência
de bits definida pelo sistema digital, basta ignorar o bit excedente à
esquerda do mais significativo da seqüência.
Overflow
• Overflow é a mudança no sinal do resultado devido a realização de
operações com números que levam ao estouro da capacidade do
registrador (sequência de bits).
• Esta situação ocorre quando se realiza operações equivalentes de
soma de dois números positivos ou de dois números negativos.
• Por exemplo, considere um registrador de 4 bits e uma representação
usando complemento de 2.
• 310 + 210 = 00112 + 00102 =
0011
+ 0010
0101 = 510 -> resultado correto!
Overflow
• 510 + 410 = 01012 + 01002 =
0101
+ 0100
1001 = -710 -> resultado ERRADO! Houve overflow! O
número 1 do bit mais significativo indica número negativo. Portanto,
pela representação de complemento de 2 o resultado obtido foi -7.
1001
– 0001
1000 -> Complementando os bits, obtém-se 01112 = +7
Overflow
• –310 – 210 = 11012 + 11102 =
1101
+ 1110
1 1011 = -510 -> resultado CORRETO! Ou seja:
1011
– 0001
1010 -> Complementando os bits, obtém-se 01012 = +5
Overflow
• –510 – 410 = 10112 + 11002 =
1011
+ 1100
1 0111 = +710 -> resultado ERRADO! Houve overflow! O
zero mais à esquerda indica que o número é positivo, portanto o
resultado obtido foi +7
Operações Numéricas
• Adição e subtração no sistema de numeração octal e hexadecimal:
• A forma mais prática de efetuar uma operação artimética em um
número octal ou hexadecimal é transformá-lo em binário, efetuar a
operação e depois reconvertê-lo para octal ou hexadecimal.
• Por exemplo:
1478
001 100 111
+ 6548
+ 110 101 100
10238
1 000 010 011
(1 0
2
3 )8
Operações Numéricas
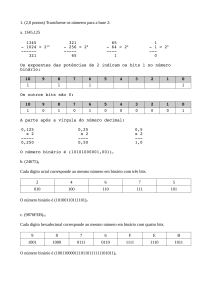
• Transformar os números octais para binário e verificar se o resultado
da operação está correto:
• 147 – 121 = 26
• 100 + 37 = 41
• 6234 – 2351 = 3663
• Transformar os números hexadecimais para binário e verificar se o
resultado da operação está correto:
• F0FC + 0A73 = FB6F
• 900 + CA1 = 15A1
• F731 – 11 = F720
• BEBE + 62DEB = 6ECA9
Resumo Sistema Num.
De
Para
Binário
Binário (base
2)
Octal (base 8)
Decimal (base
10)
Hexadecimal
(base 16)
Octal
Decimal
Hexadecimal
Agrupa 3
... +X.2y+...
Agrupa 4
...+X.8y+...
Desagrupa 3
(Desagrupa 3 /
Agrupa 4)
Converte base 2
Agrupa 4
PI / 2
PI / 8
PI / 16
PF x 2
PF x 8
PF x 16
Desagrupa 4
Converte base 2
Agrupa 3
(Desagrupa 4 /
Agrupa 3)
...+X.16y+...