9º ano – Exame 1ª Fase – 2016 – em formato word /

EXAME MATEMÁTICA – 9º ANO – 2016 – 1ª FASE
ENUNCIADO E RESOLUÇÃO (questão a questão)

Caderno 1: 35 + 10 minutos – com calculadora
Questão:
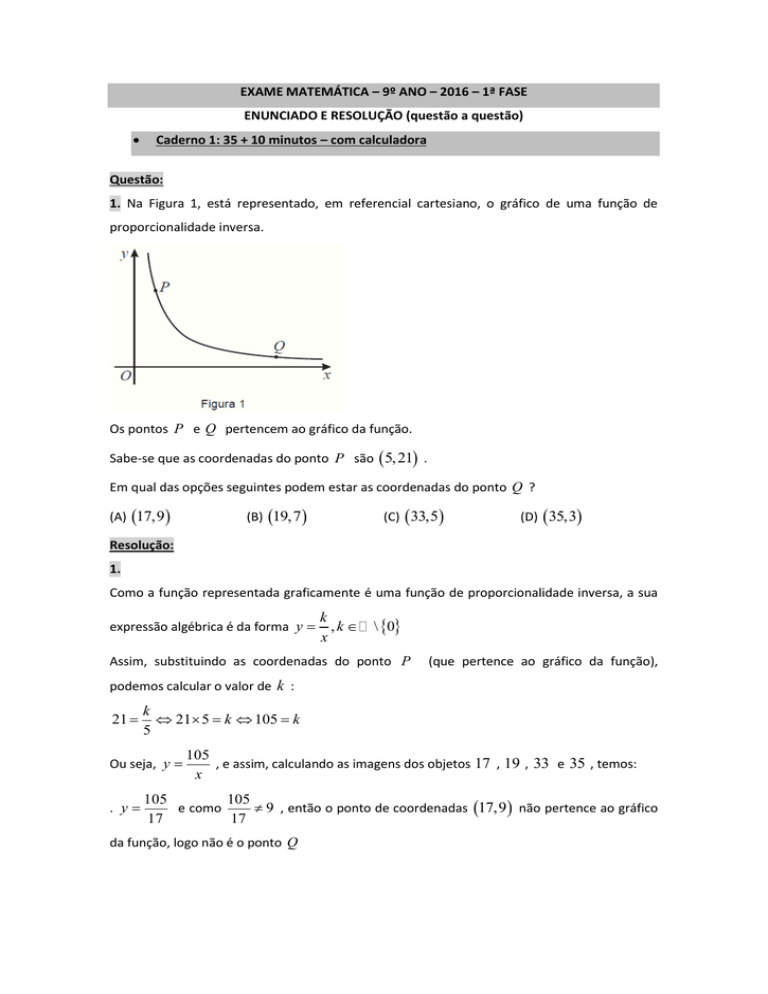
1. Na Figura 1, está representado, em referencial cartesiano, o gráfico de uma função de
proporcionalidade inversa.
Os pontos P e Q pertencem ao gráfico da função.
Sabe-se que as coordenadas do ponto P são  5, 21 .
Em qual das opções seguintes podem estar as coordenadas do ponto Q ?
(A) 17,9
(B) 19,7 
(C)  33,5
(D)  35,3
Resolução:
1.
Como a função representada graficamente é uma função de proporcionalidade inversa, a sua
expressão algébrica é da forma y 
k
,k 
x
\ 0
Assim, substituindo as coordenadas do ponto P
(que pertence ao gráfico da função),
podemos calcular o valor de k :
21 
k
 21 5  k  105  k
5
Ou seja, y 
. y
105
, e assim, calculando as imagens dos objetos 17 , 19 , 33 e 35 , temos:
x
105
105
 9 , então o ponto de coordenadas 17,9 não pertence ao gráfico
e como
17
17
da função, logo não é o ponto Q
. y
105
105
e como
 7 , então o ponto de coordenadas 19,7  não pertence ao gráfico
19
19
da função, logo não é o ponto Q
. y
105
105
e como
 5 , então o ponto de coordenadas  33,5 não pertence ao gráfico
33
33
da função, logo não é o ponto Q
. y
105
105
e como
 3 , então o ponto de coordenadas  35,3 pertence ao gráfico da
35
35
função, logo pode ser o ponto Q
Resposta: Opção (D)
Questão:
2. Na Figura 2, apresenta-se uma notícia publicada num jornal acerca dos fundos de que a ONU
(Organização das Nações Unidas) necessitava, em 2011, para atuar no combate à fome em
África.
Domingo, 7 de agosto de 2011
São precisos 1700 milhões de euros.
Até agora, a ONU só obteve 45% 45% desta verba.
Figura 2
Escreve, utilizando notação científica, o valor, em euros, de que a ONU dispunha, à data da
notícia, para atuar no combate à fome em África.
Apresenta todos os cálculos que efetuares.
Resolução:
2.
Escrevendo 1 milhão em notação científica, temos:
1000000  1106
Pelo que, 1700 milhões, em notação científica, é:
1700 1106  1,7 103 1106  1,7 103 106  1,7 1036  1,7 109
Determinando 45% deste valor, em euros, e escrevendo o resultado em notação científica,
vem que:
1, 7 109 
euros.
45
 1, 7 109  0, 45  0, 765 109  7, 65 10 1 109  7, 65 10 19  7, 65 108
100
Questão:

3. Na Figura 3, estão representadas duas retas paralelas, r e s , e duas semirretas, O C e

OD .
Sabe-se que:


. A reta r interseta as semirretas O C e O D nos pontos
A e B , respetivamente;


. A reta s interseta as semirretas O C e O D nos pontos
C e D , respetivamente;
. O ponto A pertence ao segmento de reta OC  ;
. OA  8, 0 cm , AC  4,5 cm e OB  9, 6 cm ;
A figura não está desenhada à escala.
Determina BD .
Apresenta o resultado em centímetros.
Apresenta todos os cálculos que efetuares.
Resolução:
3.
Como os triângulos  ABO e CDO são semelhantes (porque têm um ângulo comum e os
lados opostos a este ângulo – os lados  AB  e CD são paralelos).
Assim, a razão entre lados correspondentes é igual, ou seja:
OD OC

OB OA
Temos ainda que:
OC  OA  AC  8  4,5  12,5 cm
Desta forma, substituindo os valores conhecidos, vem que:
OD 12,5
12,5  9,6

 OD 
 OD  15 cm
9,6
8
8
Como OD  OB  BD  BD  OD  OB , calculando o valor de BD , em centímetros,
vem:
BD  OD  OB  15  9, 6  5, 4 cm
Questão:
4. Na Figura 4, estão representados um prisma reto  ABCDEFGH  , de bases quadradas, e
um cilindro cujas bases estão inscritas na base do
prisma.
Sabe-se que:
. AB  20 cm ;
. A diferença entre o volume do prisma e o volume
do cilindro é igual a 3000cm3 .
A figura não está desenhada à escala.
4.1. Identifica, recorrendo a letras da figura, uma
reta perpendicular ao plano que contém a base
 ABCD
do prisma.
4.2. Determina CH .
Apresenta o resultado em centímetros, arredondado às unidades.
Sempre que, em cálculos intermédios, procederes a arredondamentos, conserva, no mínimo,
duas casas decimais.
Apresenta todos os cálculos que efetuares.
Resolução:
4.1.
Como as arestas laterais de um prisma são perpendiculares às bases do prisma, também o são
relativamente ao plano que contém uma das bases do prisma.
Assim, uma reta perpendicular ao plano ABC , é, por exemplo:
a reta AF
4.2.
Como CH
é a medida da altura do cilindro e também do prisma, podemos determinar
expressões do volume do prisma VP  e do volume do cilindro VC  , em função de CH :
2
 VP  ABase  altura  AB  CH  400CH
2
2
 AB 
 20 
 VC  ABase  altura   r  CH  
  CH       CH  100 CH
 2 
 2 
2
Como a diferença dos volumes, é de 3000cm3 , vem que:
VP  VC  3000  400CH  100 CH  3000  CH  400  100   3000  CH 
Assim, o valor de CH , em centímetros, arredondado às unidades, é CH  35 cm
Questão:
5. A Figura 5 é uma fotografia do farol do Cabo de Santa Maria,
situado na Ria Formosa, na Ilha da Culatra.
A Marta e o Rui estão a fazer um trabalho de trigonometria.
A Marta colocou-se num ponto a partir do qual podia observar o
topo do farol segundo um ângulo de amplitude 60 . Fez
algumas medições e esboçou um esquema idêntico ao que se
apresenta na Figura 6.
Nesse esquema, o ponto T
corresponde ao topo do farol, o
ponto M corresponde ao ponto de observação da Marta, e o
ponto R corresponde ao ponto de observação do Rui.
O esquema não está desenhado à escala.
Relativamente ao esquema da Figura 6, sabe-se que:
.  MCT  é um triângulo retângulo;

. O ponto R pertence à semirreta M C ;
. T MC  60 e T RC  45 ;
MC  25, 6 m .
Determina MR , ou seja, determina a distância entre a Marta e o Rui.
3000
400  100
Apresenta o resultado em metros, arredondado às unidades.
Sugestão: Começa por determinar TC .
Sempre que, em cálculos intermédios, procederes a arredondamentos, conserva, no mínimo,
duas casas decimais.
Apresenta todos os cálculos que efetuares.
Resolução:
5.
O triângulo CMT  é retângulo em C . Como, relativamente ao ângulo CMT , o lado
 MC 
é o cateto adjacente e o lado TC 
é o cateto oposto, usando a definição de
tangente, temos:
tg 60 
TC
TC
 tg 60 
 25,6  tg 60  TC
25,6
MC
Como tg 60  1, 73 , vem que:
TC  25, 6 1, 73  44, 29
O triângulo CRT  é retângulo em C . Como, relativamente ao ângulo CRT , o lado CR 
é o cateto adjacente e o lado TC  é o cateto oposto, voltando a usar a definição de
tangente, temos:
tg 45 
TC
TC
 CR 
tg 45
CR
Como tg 45  1 , vem que:
CR 
44, 29
 44, 29
1
Assim, determinando o valor de MR , em metros, e arredondando o resultado às unidades,
vem que:
MR  MC  CR  25, 6  44, 29  70 m
Questão:
6. Para cada número natural n maior do que 1 , seja A  1, n  um intervalo de números


reais.
Qual é o menor valor de n para o qual o intervalo A tem, exatamente, vinte e oito números
naturais?
Resolução:
6.
Para que o intervalo A  1, n  tenha 28 números naturais,

intervalo é aberto à direita,

n  28 , porque como o
nA
Assim, como 282  784 , temos que o menor número natural que verifica a condição
n  28 é:
n  282  1  784  1  785

Caderno 1: 55 + 20 minutos – sem calculadora
Questão:
7. Na tabela seguinte apresentam-se dados relativos às idades de uma amostra de alunos do
3º ciclo de uma escola básica.
Idade (em anos)
12
13
14
15
Número de alunos
2
7
20
11
Em qual das opções seguintes se apresenta o valor do 1º quartil deste conjunto de dados?
(A) 13
(B) 13,5
(C) 14
(D) 14,5
Resolução:
7.
Como a escola tem 2  7  20 11  40 alunos, dividindo a lista ordenada em duas listas com
20 alunos cada, podemos determinar o 1º quartil, identificando a mediana do 1º conjunto.
Assim, a mediana corresponde à média das idades correspondentes às posições 10 e 11 da
lista ordenada.
Como 9 alunos têm 13 anos ou menos, e são 20 os alunos com 14 anos, as posições 10 e
11 da lista ordenada das idades são ambas 14 anos, pelo que, o primeiro quartil deste
conjunto de dados é 14 anos.
20
20
12 12 13 13 13 13 13 13 13 14 14 14 ... 14 14 ... 15 15 ... 15
10
10
10
10
Resposta: Opção (C)
Questão:
8. O António e a Beatriz estão a jogar um jogo de dados.
Em cada jogada, cada um deles lança um dado cúbico equilibrado, com as faces numeradas de
1 a 6 , e observa o número da face voltada para cima.
Em cada jogada vence aquele cujo dado apresente o maior dos dois números.
Se, numa jogada, os dois dados apresentarem o mesmo número, é declarado empate.
8.1. O António lançou o dado e obteve o número 5 .
Qual é a probabilidade de a Beatriz vencer esta jogada?
Apresenta o resultado na forma de fração.
8.2. O António e a Beatriz lançam novamente os dados.
Qual é a probabilidade de o António vencer esta nova jogada?
Apresenta o resultado na forma de fração irredutível.
Mostra como chegaste à tua resposta.
Resolução:
8.1.
A Beatriz só vence a jogada se o seu dado tiver um número maior que o número do dado do
António. Como só existe no dado uma face com um número superior a 5 , e podem sair seis
números, então o valor da probabilidade da Beatriz vencer a jogada, escrito na forma de
fração, é:
p
1
6
8.2.
Organizando numa tabela todos os conjuntos de lançamentos dos dois dados, e assinalando as
situações em que o António é vencedor  A , em que é declarado empate, e em que a Beatriz
vence  B  , temos:
Beatriz
1
2
3
4
5
6
1
Empate
B
B
B
B
B
2
A
Empate
B
B
B
B
António
3
A
A
Empate
B
B
B
4
A
A
A
Empate
B
B
5
A
A
A
A
Empate
B
6
A
A
A
A
A
Empate
Assim, é possível verificar que, de entre as 36
configurações possíveis de obter no
lançamento dos dois dados (ou seja 36 casos possíveis), em 15 delas o António tem um
número maior (ou seja 15 casos favoráveis).
Assim, recorrendo à Regra de Laplace, calculando a probabilidade de que o António vença a
nova jogada, e tornando a fração irredutível, é:
p
15 5

36 12
Questão:
9. Sejam q e r números reais, tais que q  r .
Qual das seguintes afirmações é verdadeira?
(A) 2q  2r
(B) 2q  2r
(C) q  2  r  2
(D) q  2  r  2
Resolução:
9.
Simplificando cada uma das desigualdades, temos que:
 2q  2r 
2q 2r

qr
2
r
  2q  2r   1   2q    1   2r   2q  2r 
2q 2r

qr
2
r
 q2  r 2  q22  r 22  q  r
 q2  r 2  q2 2  r 2 2  q  r
Assim, se q  r , então a afirmação 2q  2r é verdadeira.
Resposta: Opção (B)
Questão:
10. Observa as igualdades seguintes, que ilustram uma propriedade dos quadrados perfeitos
dos números naturais.
12  1
22  1  3
32  1  3  5
42  1  3  5  7
52  1  3  5  7  9
Qual é a soma dos 80 primeiros números ímpares?
Resolução:
10.
Observando a regularidade das somas apresentadas, podemos verificar que a soma dos
primeiros n números ímpares é n 2
Assim a soma dos primeiros 80 números ímpares é:
1  3  5  ...  159  802  6400
80
Questão:
11.
A reta r , representada em referencial cartesiano na Figura 7, é o gráfico de uma função afim,
f .
Sabe-se que os pontos de coordenadas  0, 1 e  5,1 pertencem à reta r .
Determina uma expressão algébrica que defina a função f .
Apresenta todos os cálculos que efetuares.
Resolução:
11.
Como a função f é uma função afim, a sua expressão algébrica é da forma f ( x)  mx  b
Como gráfico de f interseta o eixo das ordenadas no ponto de coordenadas  0, 1 , temos
que b  1
Como o ponto de coordenadas  5,1 pertence ao gráfico de f , temos que f  5  1 , e
assim, substituindo os valores conhecidos na expressão algébrica, incluindo o valor de b ,
podemos determinar o valor de m :
1  m  5 1  11  m  5 
2
m
5
Desta forma, uma expressão algébrica da função f é:
f ( x) 
2
2
x  (1)  f ( x)  x  1
5
5
Questão:
12. Escreve o número
830
40
  1 na forma de uma potência de base 2 .
30
2
Apresenta todos os cálculos que efetuares.
Resolução:
12.
Observando que 40 é um número par e por isso  1
40
 1 , escrevendo 4 na forma de uma
potência de base 2 e usando as regras operatórias de potências, temos que:
30
30
830
40
8
  1    1  430  22  2230  260
30
2
2
Questão:
13. Relativamente aos trabalhadores de uma certa empresa, sabe-se que o número de homens
é igual a um quarto do número de mulheres.
Se a empresa contratar mais 2 homens e mais 3 mulheres, o número de homens passará a
ser igual a um terço do número de mulheres.
Seja h o número de homens e seja m o número de mulheres que trabalham atualmente
nesta empresa.
Escreve um sistema de equações que permita determinar o número de homens (valor de h ) e
o número de mulheres (valor de m ) que trabalham atualmente na empresa.
Não resolvas o sistema.
Resolução:
13.
Como h é o número de homens e m é o número de mulheres. A afirmação «o número de
homens é igual a um quarto do número de mulheres» pode ser traduzida por h 
1
m
4
Se a empresa contratar mais 2 homens, o número de homens passará a ser h  2 e se a
empresa contratar mais 3 mulheres, o número de mulheres passará a ser m  3 .
Como, nestas condições, o número de homens passará a ser igual a um terço do número de
mulheres, então h  2 
1
 m  3
3
Assim, um sistema de equações que permita determinar o número de homens e o número de
mulheres, pode ser:
1

h  4 m

 h  2  1  m  3

3
Questão:
14. Resolve a equação seguinte.
x2  3  x  2  x  3
Apresenta todos os cálculos que efetuares.
Resolução:
14.
Aplicando a propriedade distributiva, escrevendo a equação na forma canónica e usando a
fórmula resolvente, vem:
x 2  3  x  2   x  3  x 2  3x  6  x  3  x 2  3x  6  x  3  0  x 2  2 x  3  0 
 a  1, b  2, c  3
2  22  4 1 3
2 
x
x
2 1
x
4  12
2  16
x

2
2
2  4
2  4
2
6
 x
x  x
 x  1  x  3
2
2
2
2
C.S.  3,1
Questão:
15. Resolve a inequação seguinte.
x 1 5x 1

6
3
Apresenta o conjunto solução na forma de intervalo de números reais.
Apresenta todos os cálculos que efetuares.
Resolução:
15.
Resolvendo a inequação, temos:
x 1 5x 1
x 1 5x 1
x  1 10 x  2





 x  1  10 x  2 
6
3
6
3 (2)
6
6
1
 x  10 x  2  1  9 x  1  9 x  1  x 
9
1

C.S .   ,  
9

Questão:
16. Na Figura 8, estão representados dois quadrados de lados OA e OB  .
Sabe-se que:
. O ponto A pertence ao segmento de reta OB 
. OA  a
. AB  b
Qual das expressões seguintes representa a área do quadrado de
lado OB  ?
(A) a 2  2ab  b 2
(B) a 2  2ab  b 2
(C) a 2  b 2
(D) a 2  b 2
Resolução:
16.
Como OB  OA  AB  a  b , temos que a área do quadrado de lado OB é:
A  OB   a  b   a 2  2  a  b  b2  a 2  2ab  b2
2
2
Resposta: Opção (A)
Questão:

17. Na Figura 9, estão representados o triângulo escaleno  LMN  , as semirretas M O e

N O , bissetrizes dos ângulos LMN e MNL , respetivamente, e a circunferência inscrita no
triângulo  LMN  .
Sabe-se que:
. A reta MN é tangente à circunferência no ponto P ;
. O ponto Q é a interseção do segmento de reta  MO com a circunferência.
17.1. Sabe-se também que OM N  15 .
Qual é a amplitude do arco QP ?
(A) 70
(B) 75
(C) 80
(D) 85
17.2. Admite que OP  3 e que PN  3 .
Determina o valor exato de ON .
Apresenta todos os cálculos que efetuares.
17.3. Como se designa o ponto O relativamente ao triângulo  LMN  ?
(A) Baricentro
(B) Circuncentro
(C) Incentro
(D) Ortocentro
Resolução:
17.1.
Como a reta MN é tangente à circunferência no ponto P , o raio OP  é perpendicular à
reta MN
Desta forma, o triângulo OPM  é retângulo em P , ou seja, OPM  90 , e assim, como
OM N  OM P  OPM  180  M OP  15  90  180  90  15 
 M OP  180  90  15  M OP  75
Como o ângulo MOP é o ângulo ao centro relativo ao arco QP , a amplitude do arco é igual
à amplitude do ângulo:
QP  75
Resposta: Opção (B)
17.2.
O triângulo
OPN 
é retângulo em P (porque o raio
OP
da circunferência é
perpendicular à reta tangente em P , que contém o lado  PN  do triângulo).
Assim, recorrendo ao Teorema de Pitágoras, temos que:
2
2
2
2
ON  OP  PN  ON 
 3
2
2
2
 32  ON  3  9  ON  12  ON  12
ON  0
17.3.
Como o ponto O é a interseção de duas bissetrizes de ângulos do triângulo  LMN  , então o
ponto O é Incentro do triângulo.
Resposta: Opção (C)