1 1 U W ∆ = ∆ +∆ 22.386 V V L = = (isocórico)⇔ PV PV

Resumo e Exemplos Resolvidos – Processos Termodinâmicos - Física – Prof. Dr. Cláudio S. Sartori
 1a Lei da termodinâmica: Q  U
 Processos termodinâmicos comuns
Processo
Estado
i f
Isotérmico a
temperatura
T
Vf
Wi  f 
 P  dV
Vi
V 
nRT ln  f 
 Vi 
Wi  f 
Adiabático
U i  f
Qi  f
0
V 
nRT ln  f 
 Vi 
Equação
de Estado
PV  nRT

1 
Wi  f  CV Ti  T f
W

nR
Ti  Tf 
 1
Isocórico ou
0
ou
0
CV T f  Ti 
CV T f  Ti 
2a Lei da Termodinâmica:
“Quando se incluem todos os sistemas que tomam
parte num processo, a entropia ou permanece constante ou
aumenta”.
“Não é possível um processo no qual a entropia
decresce”.
“É impossível qualquer transformação cujo único
resultado seja a absorção de calor de um reservatório a uma
temperatura única e sua conversão total em trabalho
mecânico”.
“É impossível qualquer transformação cujo único
resultado seja a transferência de calor de um corpo frio para
outro mais quente”.
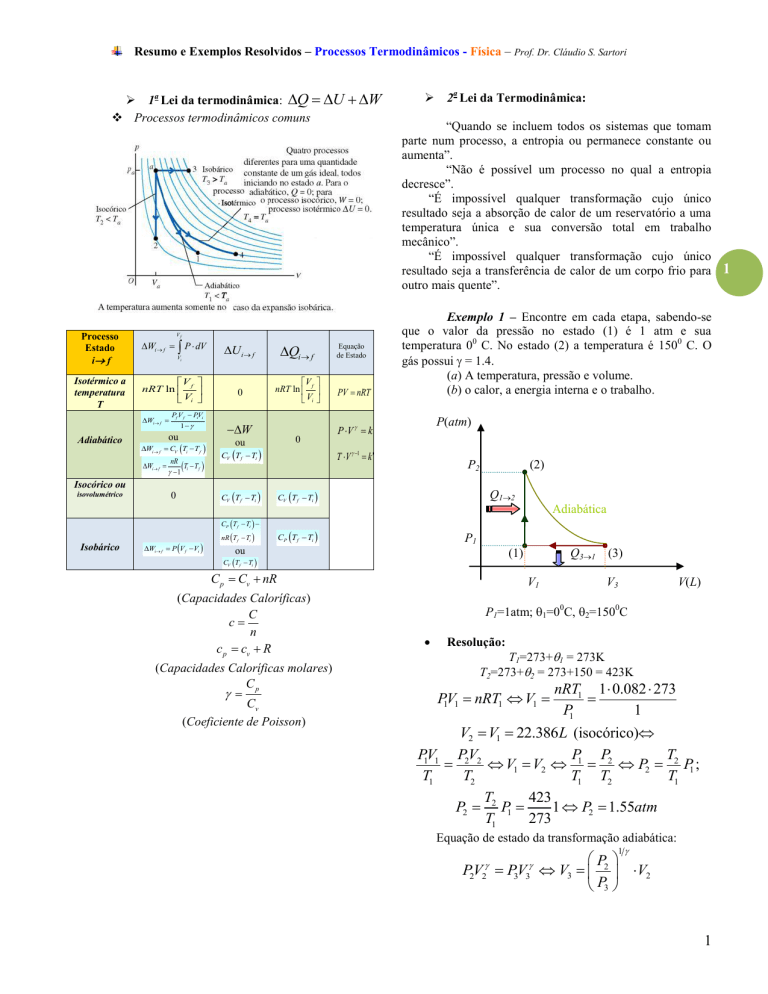
Exemplo 1 – Encontre em cada etapa, sabendo-se
que o valor da pressão no estado (1) é 1 atm e sua
temperatura 00 C. No estado (2) a temperatura é 1500 C. O
gás possui  = 1.4.
(a) A temperatura, pressão e volume.
(b) o calor, a energia interna e o trabalho.
Pf V f  PV
i i
ou
Wi  f 
isovolumétrico
 W
P(atm)
P V   k
T V  1  k 
P2
(2)
CV T f  Ti 
Q12
Adiabática
CP T f  Ti  
Isobárico
Wi  f  P V f  Vi 
nR T f  Ti 
CP T f  Ti 
P1
ou
(1)
CV T f  Ti 
C p  Cv  nR
(Capacidades Caloríficas)
C
c
n
c p  cv  R
(Capacidades Caloríficas molares)
C
 p
Cv
(Coeficiente de Poisson)
Q31
V1
(3)
V3
V(L)
P1=1atm; 1=00C, 2=1500C

Resolução:
T1=273+1 = 273K
T2=273+2 = 273+150 = 423K
nRT1 1 0.082  273

P1
1
V2  V1  22.386L (isocórico)
PV
PV
P P
T
1 1
 2 2  V1  V2  1  2  P2  2 P1 ;
T1
T2
T1 T2
T1
T
423
P2  2 P1 
1  P2  1.55atm
T1
273
PV
1 1  nRT1  V1 
Equação de estado da transformação adiabática:
1
 P2 
PV
 V2
2 2  PV
3 3  V3  
 P3 


1
1
Resumo e Exemplos Resolvidos – Processos Termodinâmicos - Física – Prof. Dr. Cláudio S. Sartori
W23  1032.72 J
1
 1.55 1.4
V3  
  22.386  V3  30.61L
 1 
PV
1 30.61
3 3
PV

 373.29 K
3 3  nRT3  T3 
nR 1 0.082
Etapa 1  2 (isocórica – Não há variação de volume)
U 23  W23
U 23  1032.72 J
Etapa 3  1 (Isobárica)
V1
W31   PdV  P  V1  V3 
V2
W12   PdV  0 ; Q12  CV T12
V3
W31  1  22.386  30.61
V1

Cp
; C p  Cv  nR
Cv
C  nR
C  1 8.31
  v
 1.4  v
Cv
Cv
1.4Cv  Cv  8.31  1.4Cv  Cv  8.31
8.31
0.4Cv  8.31  Cv 
 Cv  20.775 KJ ;
0.4
C p  Cv  nR  C p  20.775  1 8.31
Q31  29.085  273  372.29
C p  29.085 KJ
Q31  2916.93J
W31  8.224atm  L
W31  8.224 101.3
W31  833.09 J
Q31  CP T31
Q31  CP T1  T3 
Q31  W31  U31 (1a Lei da Termodinâmica)
Q12  CV T2  T1 
U31  Q31  W31
Q12  20.775  423  273
U31  2916.93   833.09
Q12  3116.25J
U31  2083.84 J
Q12  W12  U12
Q12  U12  0  U12  Q12  3116.25J
Etapa 2  3 (Adiabática: Calor nulo)
Q23  0
Q23  W23  U 23 (1a Lei da Termodinâmica)
0  W23  U 23  U 23  W23
Vf
Wi  f 

Vf
PdV 
Vi
Wi  f 
 kV

dV 
Pf V f  PV
i i
1 
Vi
nR
Pf V f  PV
i i ou
Wi  f 
T T
 1 i f
1 

Wi  f  nR

T f  Ti
T f  Ti
 Wi  f  nRCV C  C
C
V
P
1 P
CV
T  Ti
Wi  f  nRCV f
nR
Wi  f  CV Ti  T f
2
Como 1 atm.L=101.3 J

W23  CV T2  T3 
W23  20.775  423  373.29
Etapa 1  231 (Ciclo)
Q11  Q12  Q23  Q31
Q11  3116.25  0  2916.3
Q11  199 J
W11  W12  W23  W31
W11  0  1032.72  833.09
W11  199 J
U11  U12  U 23  U31
U11  311625  1032.72  2083.84
U11  0
 Resumo do Ciclo:
Etapa
W ( J )
U ( J )
Q( J )
12
23
31
1
…1
0
1032.72
-833.09
199
3116.25
-1032.72
-2083.84
0
3116.25
0
-2916.93
199
2
Resumo e Exemplos Resolvidos – Processos Termodinâmicos - Física – Prof. Dr. Cláudio S. Sartori
Exemplo 2 – Um cilindro com um pistão contém
0.150 mol de nitrogênio a uma pressão de l,80.10 5 Pa e à
temperatura de 300 K. Suponha que o nitrogênio possa ser
tratado como um gás ideal. O gás inicialmente é comprimido
isobaricamente até ocupar a metade do seu volume inicial. A
seguir ele se expande adiabaticamente de volta para seu
volume inicial e finalmente ele é aquecido isocoricamente até
atingir sua pressão inicial.
(a) Desenhe um diagrama pV para esta sequência de
processos.
(b) Ache a temperatura no início e no fim da
expansão adiabática.
(c) Calcule a pressão mínima.
Exemplo 3 – Use as condições e os processos
mencionados no Exemplo 2 para calcular:
(a) o trabalho realizado pelo gás, o calor fornecido
ao gás e a variação da energia interna durante a compressão
inicial;
(b) o trabalho realizado pelo gás, o calor fornecido
ao gás e a variação da energia interna durante a expansão
adiabática;
(c) o trabalho realizado pelo gás, o calor fornecido
ao gás e a variação da energia interna durante o aquecimento
final.

 Vb 
PV
  Pb
b b  PV
c c  Pc  
 Vc 



1
 Pc    1.8 105
2
C
  p ; C p  Cv  nR
Cv
C  nR
20.76  0.15  8.31
  v
 
   1.06
Cv
20.76
C p  Cv    20.76 1.06  C p  22.0065 KJ
1.06
1
Pc   
2
1.8 105  Pc  86333.77 Pa
1.8 105  0.00103875
 150K
0.15  8.31
86333.77  0.0020775
PV
 143.89 K
c c  nRTc  Tc 
0.15  8.31
PV
b b  nRTb  Tb 
Etapa a  b (isobárica – Não há variação de pressão)
Vb
Wa b   PdV
 Resolução:
Va
Wab  Pa Vb  Va 
P(Pa)
Wab  1.8 105  0.00103875  0.0020775
isobárica
Pi =1,8.105
(b)
(a)
Adiabática
Wab  186.525J
isocórica
Pi
Vi
Cv ( N2 )  20.76
V(m3)
J
K
n = 0.15; R=8.31J/(molK)
Pi=1,8.105Pa; Ti = Ta = 300K
PV
i i  nRTi  Vi 
Qab  CP Tb  Ta 
Qab  22.0065 150  300
(c)
Vf = Vi/2
Qab  CP Tab
nRTi 0.15  8.31 300

Pi
1.8 105
Vi  0.0020775m3
V
V 1
V f  i  b   Vc  Va  0.00103875m3
2
Vc 2
Qab  3300.975J
Qab  Wab  U ab
U ab  Qab  Wab
U ab  3300.975   186.525
U ab  3114.45J
Etapa b  c (Adiabática: Calor nulo)
Qbc
Qbc  0
 Wbc  Ubc
(1a Lei da Termodinâmica)
0  Wbc  Ubc  Ubc  Wbc
3
3
Resumo e Exemplos Resolvidos – Processos Termodinâmicos - Física – Prof. Dr. Cláudio S. Sartori
Vf
Wi  f 

Vi
Vf
PdV 
 kV

dV 
Pf V f  PV
i i
Vi
1 

nR
Pf V f  PV
i i ou
Wi  f 
T T
 1 i f
1 
nR
W 
T  T 
ou i  f CP  1 i f
CV
Wi  f 
Wi  f  nRCV
Wi  f  nRCV

Ti  T f
Onde:
CP  CV
Ti  T f
nR
Wi  f  CV Ti  T f
Exemplo 3 – Dado o Ciclo Diesel, com:
Taxa de expansão:
V
rE  a
Vc
Taxa de compressão:
V
rC  a
Vb
Va  8Vc ; Va  10Vb ;   1.4 ; Tb  350K ;
Vb  2.5 103 m3 ; n  2.5
4
e seu rendimento dado por:

1 1 rE   1 rC 
  1
 1 rE   1 rC 

Wbc  CV Tb  Tc 
Wbc  20.76 150  143.89
Wbc  126.8436 J
Ubc  Wbc
Ubc  126.8436 J
Etapa c  a (Isocórica Vca = 0)

Determine:
(a) As temperaturas, volume e pressão nas etapas a, b e
c.
(b) O trabalho, o calor e a energia interna em cada etapa.
O rendimento  do ciclo.
Dados:  
CP
; CP  CV  nR ; PV  nRT ;
CV
PV
b b  nRTb
Wca  0 J
Qca  CV  Ta  Tc 
Qca  20.76   300  146.39
Qca  3240.84 J
Qca  Wca  U ca
(1a Lei da Termodinâmica)
3240.84  0  U ca
U ca  3240.84 J
Etapa 1  …1
Somas
Etapa
W ( J )
U ( J )
Q( J )
ab
b c
ca
-186.525
126.844
0
-60
-3114.45
-126.844
3240.84
0
-3300.975
0
3240.84
-60
a  … a
Vb
 Resolução:
(a) Va  8Vc ;
Vc
Va
Va  10Vb ;   1.4 ; Tb  350K ;
Vb  2.5 10 m ; n  2.5
3
3
Va  10Vb  10  2.5 103  Va  2.5 102 m3
Va  8Vc  Vc 
Va 2.5 102

8
8
 Vc  3.125 103 m3
4
Resumo e Exemplos Resolvidos – Processos Termodinâmicos - Física – Prof. Dr. Cláudio S. Sartori
U ab  Wab
Vb Vc
V
  Tc  c Tb
Tb Tc
Vb
Tc 
 U ab  10939.57 J
3
3.125 10
350  Tc  437.5K
2.5 103


 1
PV
a a  PV
b b  TaVa
 Etapa b  c: Expansão isobárica.
 1
 TbVb
Vc
Wbc   PdV
 1
V 
 Ta   b 
 Va 
Vb
Tb
Wbc  Pb Vc  Vb   nR Tc  Tb 
Wbc  2.5  8.31  437.5  350
1.4 1
1
Ta    350
 10 
Ta  139.34K


 1
PV
c c  PdVd  TcVc
Qbc  CP Tbc
 Qbc  CP Tc  Tb 
 1
 TdVd
Qbc  72.71  350  139.34
 1
V 
 Td   c 
 Vd 
Tc
 Qbc  6362.125J
Qbc  Wbc  Ubc
 Ubc  Qbc  Wbc
1.4 1
1
Td    437.5
8
Td  190.43K
(b)
C
  P ; CP  CV  nR
CV
C
1.4  P  CP  1.4CV
CV
1.4CV  CV  2.5  8.31  1.4CV  CV  20.775
20.775 
CV  51.93 KJ
0.4CV  20.775  CV 
0.4
CP  1.4CV  CP  1.4  51.93  CP  72.71 KJ
 Etapa a  b: Compressão adiabática.
Qab  0
Qab  Wab  U ab (1a Lei da Termodinâmica)
0  Wab  U ab  U ab  Wab
Wi  f 
Wi  f
Vf
Vf
Vi
Vi
 PdV   kV
P V  PV
i i ou
 f f
1 

dV 
Wi  f  nR
5
 Wbc  1817.81J
Pf V f  PV
i i
C
U bc  CP Tc  Tb  - nR Tc  Tb  =
 nR  Tc   C p  nR  Tb  Cv Tc  Tb 
p
Ubc  Cv  Tc  Tb 
Ubc  6362.125  1817.81
 Ubc  4544.315J
 Etapa c  d: Expansão adiabática.
Qcd
0  Wcd  U cd  U cd  Wcd
Vf
Wi  f 

Vf
PdV 
Vi

dV 
Pf V f  PV
i i
1 
Pf V f  PV
i i ou W
i f
1 
 nR
Wi  f  CV  Ti  T f
T f  Ti
T f  Ti

1   ou
Wcd  CV  Tc  Td 
1 
Wcd  51.93  437.5  190.43
Wi  f  CV Ti  T f   Wab  CV Ta  Tb 
Wab  10939.57 J
 kV
Vi
Wi  f 
1 
Wab  51.93 139.34  350
Qcd  0
 Wcd  U cd (1a Lei da Termodinâmica)
 Wcd
U cd
 12830.34 J
 Wcd  U cd  12830.34 J
5
Resumo e Exemplos Resolvidos – Processos Termodinâmicos - Física – Prof. Dr. Cláudio S. Sartori
 Etapa d  a: isocórico.
Wd a 
1 T  T 
  1  d a 
  Tc  Tb 
Va
 PdV  0
Na expansão adiabática:
Vd
Qd a  CV Tda  Qd a  CV Ta  Td 
Qd a  51.93  139.34  190.43
bc
expansão
isobárica
U ( J )
CV Tb  Ta 
Q( J )
-10939.57
10939.57
Pb Vc  Vb  
CP Tc  Tb 
0
CP Tc  Tb 
6362.125
QH
nR Tc  Tb  =
1817.81
C  nR T 
 C  nR  T 
p
c
p
CV Tc  Td 
cd
expansão
adiabática
12830.34
da
isocórica
0
a  … a
b
Cv Tc  Tb  
4543.875
CV Td  Tc 
0
12830.34
CV Ta  Td 
CV Ta  Td 
-2653.103
-2653.103
0
3709.022
QC
3708.583709
Observe que:

Wciclo
QH
C T  T   nR Tc  Tb   CV Tc  Td 
 V a b
CP Tc  Tb 
nR CV  Ta  Tb   Tc  Td  



CP CP 
Tc  Tb 

C C
C  T  T   Tc  Td  
 P V  V  a b

CP
CP 
Tc  Tb 

1 1  T  T   Tc  Td  
  1   a b

 
Tc  Tb 

1  T  T   Tc  Td  
  1  1  a b


Tc  Tb 

1  Tc  Tb   Ta  Tb   Tc  Td   
  1 

 
Tc  Tb 


 rE 1  Td  rE1 Tc Na
T V 
TaVa  TbVb  a   b   rC 1  Ta  rC1 Tb
Tb  Va 
Vc
1
Vb Vc
T V V
r
T r
r
  c  c  a  E  C  c  C
1 rE
Tb Tc
Tb Vb Vb
Tb rE
rc
Va
 1
W ( J )
CV Ta  Tb 
nR Tc  Tb 
 TcVc
T V 
 c  d 
Td  Vc 
 1
U d a  2653.103J
ab
Compressão
adiabática
TdVd
 1
compressão adiabática:
 Qd a  2653.103J
Etapa
 1
 1
 1
6
1  rE1 Tc  rC1 Tb 
  1 

  Tc  Tb

 1 Tc

rE
 rC1 

Tb
1

  1 
  Tc  1 


Tb
 rE rC rC
 1 rC


rE
 rC1 

rE
1  rE rE rC
1
   1 
  1 
  rC  1 
  rC  rE



rE
rE

 1 1 
rC 
1  rE rC 

  1 
  rC  rE 


rE
1 1

1  rE rC
  1 
  rC  rE
 rC rE
1 1

1  rE rC
  1 
 11
 rE rC















Chega-se, portanto, a:
1  1 r   1 rC 
  1  E
  1 rE   1 rC 





6
Resumo e Exemplos Resolvidos – Processos Termodinâmicos - Física – Prof. Dr. Cláudio S. Sartori

 Resolução:
(a)
 Etapa a  b: Compressão adiabática
Wciclo 3709

 58%
QH
6362
Podemos calcular também, sabendo que:
rE 
Va
V
 8 ; rC  a  10 ;   1.4
Vc
Vb


1  1 rE   1 rC  
  1
  1 rE   1 rC  


1.4
1.4
1  1 8   1 10  
  1
1.4  1 8   1 10  


1  1 8   1 10 
  1
1.4  1 8   1 10 

  58%
1.4
1.4




(a) O trabalho, a energia interna e o calor em cada
etapa.
(b) O rendimento do ciclo.
Vb
Va
é chamada de razão de compressão.
Assim:
  1
1
r
 1
 TbVb
V 
 Ta   b 
 Va 
 1
1
Tb  Ta   
r
Tb
1.4 1
1
Ta   
9
350  Ta  145.33K
Vf
n = 2.5 e r = 9
Vb  2.5 103 m3 . Determine:

TaVa
 1
Qab  0
Qab  Wab  U ab (1a Lei da Termodinâmica)
0  Wab  U ab  U ab  Wab
Exemplo 4 – Dado o Ciclo Otto do motor a
gasolina, com: Tb  350 K e Tc  600 K
Dados: A razão: r
 1
 1
Wi  f 

Vf
PdV 
Vi
Wi  f 
 kV

dV 
Pf V f  PV
i i
1 
Vi
Pf V f  PV
i i ou
1 
Wi  f  nR
7
T f  Ti
1 
Wi  f  CV Ti  T f
ou

 Wa b  CV Ta  Tb 
CP
CV
CP  CV  nR
C
1.4  P  CP  1.4CV ;
CV
1.4CV  CV  2.5  8.31  1.4CV  CV  20.775
20.775
0.4CV  20.775  CV 
0.4
CV  51.93 KJ
CP  1.4CV
CP  1.4  51.93
CP  72.71 KJ
 
Wab  51.93 145.33  350
Wab  10628.5J
U ab  Wab  U ab  10628.5J
 Etapa b  c: Aumento isocórico de volume
Vc
Wbc   PdV  0
Vb
Qbc  CV Tbc  Qbc  CV Tb  Tc 
nRTb
PV
b b  nRTb  Pb 
Vb
7
Resumo e Exemplos Resolvidos – Processos Termodinâmicos - Física – Prof. Dr. Cláudio S. Sartori
2.5  8.31 350
 Pb  2908kPa
2.5 103
Va  rVb  Va  2.5 102 m3
nRTa
PV
a a  nRTa  Pa 
Va
2.5  8.31145.33
Pa 
 Pa  120769.23Pa
2.5 102
Pb 
 1
 1
TcVc
 1
 Td Vd
V 
 Td   c 
 Vd 
 1
1
Tc  Td   
r
Tc
1.4 1
1
Td   
9
600  Td  249 K
Qbc  51.93   600  350 
Qbc  12982.5J
Ubc  12982.5J
 Etapa c  d: Expansão adiabática
Qcd  0
Qcd  Wcd  U cd (1a Lei da Termodinâmica)
0  Wcd  U cd  U cd  Wcd
Wi  f 
Wi  f 
Vf
Vf
Vi
Vi
 PdV   kV

Pf V f  PV
i i ou W
i f
1 
dV 
 nR
Pf V f  PV
i i
1 
T f  Ti
1 
Wi  f  CV Ti  T f
ou

Wcd  51.93  600  249 
Wcd  18227.43J
U cd  Wcd
U cd  18227.43J
 Etapa d  a: Queda isocórica
Va
 PdV  0
Vd
Qd a  CV Tda  Qd a  CV Ta  Td 
Qd a  51.93  145.33  249
Qd a  5383.58J
U d a  5383.58J
cd
expansão
queda de
temperatura de
Tc a Td
da
queda
isocórica da
temperatura
abc
da
W(J)
U(J)
Q(J)
CV (Ta  Tb )
CV (Tb  Ta )
-10628.5
0
10628.5
0
QH  CV Tc  Tb 
12982.5
QH  CV Tc  Tb 
CV (Tc  Td )
CV (Td  Tc )
18227.43
-18227.43
0
12982.5 8
QC  CV Ta  Td 
QC  CV Ta  Td 
0
-5383.58
-5383.58
CV (Ta  Tb ) +
0
CV (Tc  Td )
CV Tc  Tb  +
CV Ta  Td 
7598.9
7598.93
(b) Cálculo do rendimento:
  1
QC
QH
QH  Cv Tc  Tb  e QC  Cv Ta  Td 
Wcd  CV Tc  Td 
Wd a 
Processo
Estado
(PiViTi)
ab
Compressão
Adiabática
Tb>Ta
bc
absorção de
calor QH
  1
Td  Ta
Tc  Tb
Como: TaVa 1  TbVb 1 ; TcVb 1  TdVa 1
Por subtração: Td  Ta Va 1  Tc  Tb Vb 1 
  1
Td  Ta
Tc  Tb
 1
V 
 b 
 Va 
1
r
  1
 1
1
1.4 1
9
  0.5847
  58.47%
QC
QH
5383.58
  1
12982.5
  58%
  1
8
Resumo e Exemplos Resolvidos – Processos Termodinâmicos - Física – Prof. Dr. Cláudio S. Sartori
Wciclo
QH
7598.93

   58%
12982.5

Exemplo 5 – No ciclo de Stirling, os calores
transferidos no processos b → c, e d → a não envolvem
fontes de calor externas, porém usam a regeneração: a
mesma substância que transfere calor ao gás dentro do
cilindro no processo b → c também absorve calor de
volta do gás no processo d → a. Portanto, os calores
transferidos Qb→c, e Qd→a não desempenham pape! na
determinação da eficiência da máquina. Explique esta
última afirmação comparando as expressões de Qb→c, e
Qd→a, obtidas na parte (a),
Calcule a eficiência de um ciclo Stirling em termos das
temperaturas T1 E T2. Como ele se compara com a
eficiência de um ciclo de Camot operando entre estas
mesmas temperaturas? (Historicamente o ciclo Stirling
foi deduzido antes do ciclo de Carnot.) Este resultado
viola a segunda lei da termodinâmica? Explique.
Infelizmente a máquina que funciona com o ciclo
Stirling não pode atingir esta eficiência, devido a
problemas oriundos de transferência de calor e perdas de
pressão na máquina.
QH
Processo / Estado
(PiViTi)
ab
Compressão
Isotémica T1
bc
aumento isocórico
da temperatura e
pressão produzido
pela absorção de
calor QH
cd
expansão
isotérmica
da
queda
isocórica
quase estática da
temperatura
e
pressão de T2 a T1
abcd
a
W(J)
nRT1 ln
1
r
U(J)
Q(J)
QC  nRT1 ln
0
1
r
0
Cv T2  T1 
Cv T2  T1 
nRT2 ln r
0
QH  nRT2 ln r
0
1
+
r
nRT2 ln r
nRT1 ln
Cv T1  T2 
Cv T1  T2 
0
QC+QH
1
Q
r
  1 C    1
nRT2 ln r
QH
nRT1 ln
T1 ln r 1
T2 ln r
T ln r
   1 1
T2 ln r
T
   1 1
T2
   1
QC
9
9
Resumo e Exemplos Resolvidos – Processos Termodinâmicos - Física – Prof. Dr. Cláudio S. Sartori
Exemplo 6 – Processos termodinâmicos para um
refrigerador. Um refrigerador opera mediante o ciclo
indicado na Figura. Os processos de compressão (d→a)
e expansão (b→c) são adiabáticos. A pressão, a
temperatura e o volume do refrigerante em cada um dos
quatro estados a, b, c e d são dados na tabela abaixo.
Estado
T(°C)
P(kPa)
V (m3)
U(kJ)
a
80
2305
0,0682
1969
Per
cen
de
tag
liqu
em
0
ido
b
c
d
80
5
5
2305
363
363
0,00946
0,2202
0,4513
1171
1005
1657
100
54
5
(a) Em cada ciclo, qual é o calor retirado do interior
do refrigerador para o líquido refrigerante enquanto ele se
encontra no evaporador?
(b) Em cada ciclo, qual é o calor rejeitado do
refrigerante para fora do refrigerador enquanto o refrigerante
está no condensador?
(c) Em cada ciclo, qual é o trabalho realizado pelo
motor que aciona o compressor?
(d) Calcule o coeficiente de performance do
refrigerador.
 Etapa a  b: Condensador:
Compressão Isobárica
Vf
Wi  f 
Vb
 PdV   PdV  P Vb  Va   nR Tb  Ta 
Vi
Va
Wab  nR Tb  Ta 
Qab  CP Tb  Ta 
Qab  Wab  U ab  U ab  Qab  Wab
U ab  CP Tb  Ta   nR Tb  Ta 
U ab  Tb  CP  nR   Ta  CP  nR 
U ab  CV Tb  Ta 
10
 Etapa b  c: Válvula de expansão:
Adiabática
Qbc  0
Qbc  Wbc  Ubc (1a Lei da Termodinâmica)
0  Wbc  Ubc  Ubc  Wbc
Wi  f  CV Ti  T f

Wbc  CV Tb  Tc 
Ubc  CV Tc  Tb 
 Etapa c  d: Evaporador:
Expansão Isobárica
Wi  f 
QC
Vf
Vd
Vi
Vc
 PdV 
 PdV  P V
d
 Vc   nR Td  Tc 
Wcd  nR Td  Tc 
Qcd  CP Td  Tc 
Qcd  Wcd  U cd  U cd  Qcd  Wcd
U cd  CP Td  Tc   nR Td  Tc 
Ucd  Td  CP  nR   Tc CP  nR 
U cd  CV Td  Tc 
 Etapa d  a: Compressor:
Compressão Adiabática
Qd a  0
Qd a  Wd a  U d a (1a Lei da Termodinâmica)
0  Wd a  U d a  U d a  Wd a
QH
Wi  f  CV Ti  T f

Wd a  CV Td  Ta 
U d a  CV Ta  Td 
 a  b c d a: Ciclo
Wciclo  nR Tb  Ta   CV Tb  Tc  
nR Td  Tc   CV Td  Ta 
10
Resumo e Exemplos Resolvidos – Processos Termodinâmicos - Física – Prof. Dr. Cláudio S. Sartori
Wciclo   nR  CV  Tb   nR  CV  Ta 
Td  nR  CV   Tc  nR  CV 
(a)
Wciclo  C pTb  C pTa  C pTd  C pTc
Wciclo  C p Tb  Ta  Td  Tc 
Processo / Estado
(PiViTi)
ab
Compressão
Isobárica
bc
Expansão
adiabática
cd
Expansão isobárica
da
Compressão
adiabática
Ciclo
abcd
a
W(J)
U(J)
 Resolução:
PV  nRT  Va 
n  R  TH
Pa
0.2  8.31 400
 Va  6.648 104 m3
106
Vb  2 Va  1.3296 103 m3
n  R  TQ
PV  nRT  Pb 
Vb
0.2  8.31 400
Pb 
 Pb  5.00 105 Pa
1.3296 103
Va 
Q(J)
nR Tb  Ta 
CV Tb  Ta  QH  CP Tb  Ta 
CV Tb  Tc 
CV Tc  Tb 
0
nR Td  Tc 
CV Td  Tc 
QC  CP Td  Tc 
CV Td  Ta 
CV Ta  Td 
0
C p Tb  Ta  Td  Tc 
0
QH  QC
Exemplo 7 – Ciclo de Carnot. Uma quantidade de 0.2
mol de gás com  = 1.4 efetua o ciclo de Carnot
representado. A temperatura da fonte quente é TQ = 400K e a
temperatura da fonte fria TF = 300K. Sabendo que a pressão
inicial é de Pa = 106 Pa e que o volume dobra na expansão
isotérmica, encontre:
(a) A temperatura, o volume e a pressão nos estados a, b,
c e d.
(b) O trabalho, o calor e a energia interna em cada etapa.
(c) o seu rendimento .
11
Tb Vb 1  Tc Vc 1
1
 T   1
Vc   b  Vb
 Tc 
1
 TQ   1
Vc    Vb
 TF 
1
 400 1.41
Vc  
1.3296 103

 300 
Vc  2.7294 103 m3
PV  nRT  Pc 
Pc 
n  R  TF
Vc
0.2  8.31 300
 Pc  1.8267 105 Pa
3
2.7294 10
Td Vd 1  Ta Va 1
1
 T   1
Vd   a  Va
 Td 
1
 T   1
Vd   Q  Va
 TF 
1
 400 1.41
Vd  
 6.648 104

 300 
Vd  1.3647 103 m3
PV  nRT  Pd 
Pd 
n  R  TF
Vd
0.2  8.31 300
 Pd  3.65355 105 Pa
3
1.3647 10
11
Resumo e Exemplos Resolvidos – Processos Termodinâmicos - Física – Prof. Dr. Cláudio S. Sartori
U d a  Wd a
nR
Wi  f 
T  T 
 1 i f
nR
Wd a 
T  T 
 1 d a
0.2  8.31
Wbc 
 300  400
1.4  1
(b)
 Etapa a  b: Expansão isotérmica
U ab  0
Qab  Wab  U ab (1a Lei da Termodinâmica)
Qab  Wab  0  Qab  Wab
Vf
Wi  f 

Vi
n  R  TQ
V 
dV  n  R  TQ  ln  f 
V
 Vi 
Vi
Wi  f  0.2  8.31 400  ln  2
Vf
PdV 

Wbc  415.5J
Wi  f  460.80 J
Qab  460.80 J
Ubc  415.5J
 Etapa b  c: Expansão adiabática
Qbc  0 J
0  Wbc  Ubc (1a Lei da Termodinâmica)
Ubc  Wbc
nR
Wi  f 
T  T 
 1 i f
nR
Wbc 
T  T 
 1 b c
0.2  8.31
Wbc 
 400  300 
1.4  1
Adiabáticas: P V   K  T V  1  cte ;Q = 0
Isotérmicas PV  nRT : (Gás ideal) U = 0
C (Coeficiente de Poisson)
  P
CV
W
U
Q
nRTH ln VVba
0
nRTH ln VVba
Processo
/ Estado
(PiViTi)
ab
460.8
bc
Wbc  415.5J
Ubc  415.5J
PcVc  PbVb
=
1
CV (TH  TC )
460.8=QH
CV (TC  TH )
U cd  0
Qcd  Wcd  U cd (1a Lei da Termodinâmica)
Qcd  Wcd  0  Qcd  Wcd
Vf
Wi  f 

Vi
Vf
PdV 

Vi
n  R  TQ
V
V 
dV  n  R  TF  ln  f 
 Vi 
V 
Wcd  n  R  TF  ln  d 
 Vc 
 1.3647 
Wcd  0.2  8.31 300  ln 
 2.7294 
Wcd  345.6 J
0
-415.5
415.5
cd
nRTC ln VVdc
0
-345.6
 Etapa c d: Compressão isotérmica
12
da
a
b...
a
nRTC ln VVdc
-345.6
CV (TC  TH )
CV (TH  TC )
-415.5
415.5
0
Área do ciclo A
115.2
0
A
115.2
  1
QF Wciclo 115.8


 25%
QQ
QQ
460.8
  1
TF
300 1
 1
  25%
TQ
400 4
Qcd  345.6 J
 Etapa d  a: Compressão adiabática
Qd a  0 J
0  Wd a  U d a (1a Lei da Termodinâmica)
12
Resumo e Exemplos Resolvidos – Processos Termodinâmicos - Física – Prof. Dr. Cláudio S. Sartori
Exemplo 8 - n = 0.04 moles de ar ( = 1.4)
executam o ciclo diesel com taxas: rE = 8 e rC = 10; (taxas de
expansão e compressão, respectivamente).
Sabe-se que no estado a a temperatura é a = 27°C e
a pressão Pa = 1atm;
1.4
0.04  8.31
1.4  1
J
CP  1.1634
mol
CP 
Processo
Estado (PiViTi)
ab
compressão
adiabática
Vf
 PdV
Wi f 
Ui f  CV  Tf  Ti 
Qi f  Wi f  Ui f
(J)
(J)
(J)
CV  Ta  Tb 



CV  Tb  Ta 



0
Vi
0.831 300753.57 376.91
bc
isobárica
376.91
QH
62.62

Pc  Vc  Vb 
13
CP  Ta  Tb 



156.55




CV  Tc  Tb 
1.1634 941.96753.57 

219,17
n  R  (Tc  Tb )
(a) Determine o volume Va, Vb e Vc.
(b) Encontre as pressões e as temperaturas nos
estados a, b, c e d.
(c) Encontre o trabalho, o calor e a energia interna
em cada etapa.
(d) Determine o rendimento do ciclo.
cd
expansão
adiabática
da
isocórica
CV  Tc  Td 



CV  Td  Tc 



0
C
Ta  Td)
V  (

C
Ta  Td)
V  (

442.06
442.06
0
a  ...a
QC
91.41
A  Wciclo


91.41
QH  QC



0
127.7
127.77

Solução:
Va 
1  1 r   1 rC 
  1  E
  1 rE   1 rC 

n  R  Ta
0.04  0.082  300
 Va 
Pa
1
Va  0.98L
Va
0.984
 Vb 
 Vb  0.0984L
rC
10
V
0.984
Vc  a  Vc 
 Vc  0.123L
rE
8
Vb 
  1
r
10
Tc  c Tb  Tc  753.57  Tc  941.96K
re
8
Tc
941.95
 Td  1.41  Td  410K
rE 1
8
Pc
25.12
Pd    Pd  1.4  Pd  1.366atm
rE
8
Td 
a
b
c
d
CV 
CV 
P
(atm)
1
25.12
1.366
1.4
1.4
1  1 8   1 10  


1.4  1 8   1 10  
1  0.054409  0.0398107 

1.4 
0.025
  1  0.41709    58%
Tb  rC 1  Ta  Tb  101.41  300  Tb  753.57K
V
(L)
0.98
0.0984
0.123
0.98



  1
Pb  rC  Pa  Pb  101.4 1  Pb  25.12atm
Processo / Estado
(PiViTi)

T
(K)
300
753.57
941.96
410

Wciclo
127.77
 
   58.3%
QH
219.17
Exemplo 9 n = 0.04 moles de ar ( = 1.4) executam
o ciclo Otto com taxas: r = 10; (taxa de compressão).
Sabe-se que no estado a a temperatura é a = 27°C e
a pressão Pa = 1atm e após a explosão a pressão aumenta 2
atm.
nR
 1
0.04  8.31
J
 CV  0.831
1.4  1
mol
CP 

n R
 1
13
Resumo e Exemplos Resolvidos – Processos Termodinâmicos - Física – Prof. Dr. Cláudio S. Sartori
(a) Determine o volume Va eVb.
(b) Encontre as pressões e as temperaturas nos
estados a, b, c e d.
(c) Encontre o trabalho, o calor e a energia interna
em cada etapa.
(d) Determine o rendimento do ciclo.

Processo
Estado (PiViTi)
ab
compressão
adiabática
bc
isocórica
Solução:
Va 
Vb 
n  R  Ta
0.04  0.082  300
 Va 
Pa
1
Va  0.98L
Va
0.984
 Vb 
 Vb  0.0984 L
r
10
a  b : Pb  r   Pa  Pb  101.4 1  Pb  25.12atm
Pc  Pb  2  Pc  25.12  2  Pc  27.12atm
Tb  r  1  Ta  Tb  101.41  300  Tb  753.57K
b  c:
Tc 
Ui f  CV  Tf  Ti 
Qi f  Wi f  Ui f
(J)
(J)
CV  Ta  Tb 



CV  Tb  Ta 



0
0

49.86


CV  Tc  Tb 
(J)
0.831 300753.57 376.91
cd
expansão
adiabática
da
isocórica
a  ...a
CV  Tc  Td 



406.92
0
a
b
c
d
0.0984
0.98
CV 
CV 
P
(atm)
1
25.12
27.12
1.079
nR
 1
0.04  8.31
J
 CV  0.831
1.4  1
mol
CP 

n R
 1
1.4
0.04  8.31
1.4  1
J
CP  1.1634
mol
CP 
T
(K)
300
753.57
813.57
323.89
49.86
0
C
Ta  Td)
V  (

C
Ta  Td)
V  (

14
406.92
19.852
0
QC
19.852
QH  QC



30.01
Wciclo
30.01
 
   60.12%
QH
49.86
1
r  1
1
  1  1.41
10
  60.12%
  1
Pc
27.12
 Pd  1.4  Pd  1.079atm
r
10
V
(L)
0.98
CV  Ta  Tb 



CV  Td  Tc 



30.01
Tc
813.57
 Td  1.41  Td  323.89K
r  1
10
Processo / Estado
(PiViTi)
376.91
A  Wciclo


Pd Pa
T
323.89
  Pd  d Pa  Pd 
1  Pd  1.079atm
Td Ta
Ta
300
Pd 
 PdV
Vi
QH

27.12
753.57  Tc  813.57 K
25.12
c  d : Td 
d  a:
Pb Pc
P
  Tc  c Tb
Tb Tc
Pb
Vf
Wi f 
Exemplo 10 - Uma máquina de Carnot cujo
reservatório quente está a uma temperatura de 620 K absorve
550 J de calor nesta temperatura em cada ciclo e fornece 335
J para o reservatório frio.
(a) Qual é o trabalho produzido pela máquina
durante cada ciclo?
(b) Qual é a temperatura da fonte fria?
(c) Qual é a eficiência térmica do ciclo?
(d) Adotando:
n = 0.05 e  = 1.4 e Va = 0.01m3, encontre as
pressões e os volumes nos pontos a, b, c e d.
(e) Determine o trabalho, o calor e a energia interna
em cada etapa do ciclo de Carnot dado.

Solução:
(a) Wciclo  QH  QC  Wciclo  620  335
Wciclo  245J
Wciclo
Q  QC
  H
(c) 
QH
QH
QC
QC
;  1 
QH
QH
335
215
  1
   0.39
; 
550
550
  1
14
Resumo e Exemplos Resolvidos – Processos Termodinâmicos - Física – Prof. Dr. Cláudio S. Sartori
TC
TH
T
T
0.39  1  C  C  1  0.39
620
620
TC
 0.61  TC  378.2 K
620
V 
(d) QH  n  R  TH  ln  b 
 Va 
(b)
 1
Pd 
Estado
V 
550  0, 05  8.31 620  ln  b 
 Va 
V 
ln  b   2.135
 Va 
Vi(m³) Pi (Pa) Ti (K) Vf(m³) Pf (Pa)
Tf (K)
a -> b: isotérmica:
expansão
0,01
25761
620
0,08457 3046,
b -> c: adiabática
:expansão
0,08457
3046
620
0,29099
540
378,2
c -> d: isotérmica
:compressão
0,2909 540,00
378
0,034
4566,
378,2
d -> a: adiabática
:compressão
0,0344
378
0,01
25761
620
4566
620
Matriz: E,W,Q[6,4]
Trabalho Energia
(J)
Interna (J)
Etapa
Calor (J)
a -> b: isotérmica: expansão
549,99
0
549,99
 Vb  2.135
 e
 Va 
b -> c: adiabática :expansão
251,2
-251,2
0
c -> d: isotérmica
:compressão
-335,497
0
-335,49
 Vb 
   8.457
 Va 
c -> d: adiabática
:compressão
-251,2
251,2
0
Ciclo de Carnot
214,49
0
214,498
Rendimento
39 %
Vb  8.457 Va
1
 T   1
TH Vb 1  TC Vc 1  Vc   H  Vb
 TC 
1
 620 1.41
Vc  
 0.08457  Vc  0.2909m3

378.2


n  R  TC
0.05  8.31 378.2
Pc 
 Pc 
Vc
0.2909
Pc  540.19Pa
1
 T   1
TC Vd 1  TH Va 1  Vd   H  Va
 TC 
 620 1.41
Vd  
 0.01  Vd  0.0344m3

 378.2 
Ciclo de Carnot

P (Pa)
Vb  8.457  0.01  Vb  0.08457m3
n  R  TH
0.05  8.31 620
Pa 
 Pa 
Va
0.01
Pa  25761Pa
n  R  TH
0.05  8.31 620
Pb 
 Pb 
Vb
0.08457
Pb  3046.12Pa
1
n  R  TC
0.05  8.31 378.2
 Pc 
Vd
0.0344
Pd  4568.08Pa
20.000
10.000
0,034
4.566,854
0,291
540,009
0
0,05
0,1
g a -> b: isotérmica: expansão
b
c
d
e
f
b c -> d: isotérmica :compressão
c
d
e
f
g
b b -> c: adiabática :expansão
c
d
e
f
g
b Series9
c
d
e
f
g
0,15
V (m³)
0,2
0,25
g c -> d: adiabática :compressão
b
c
d
e
f
b c -> d: adiabática :compressão
c
d
e
f
g
b c -> d: adiabática :compressão
c
d
e
f
g
b Series16
c
d
e
f
g
Exemplo 11 - Comparação entre processos
termodinâmicos. Um cilindro contém l,20 mol de gás ideal
monoatômico inicialmente a uma pressão de 3,60.10 5 Pa e à
temperatura de 300 K e se expande até o triplo do seu
volume inicial. Calcule o trabalho realizado pelo gás quando
a expansão é:
(a) isotérmica;
(b) adiabática;
(c) isobárica;
(d) Usando um diagrama pV, indique cada um
destes processos. Em qual deles o trabalho realizado pelo gás
possui o maior valor absoluto? E o menor valor absoluto?
(e) Em qual destes processos o calor trocado possui
o maior valor absoluto? E o menor valor absoluto?
(f) Em qual destes processos a variação da energia
interna possui o maior valor absoluto? E o menor valor
absoluto?
15
15
Resumo e Exemplos Resolvidos – Processos Termodinâmicos - Física – Prof. Dr. Cláudio S. Sartori
 Solução
(a) A que temperatura correspondem os pontos A, B
E,W,Q[5,4]
e C?
Calor
(J)
a -> b: isotérmica:
expansão
3286,60
0
3286,60
a -> b: adiabática
:expansão
2330,08
-2330,08
0
a -> b: isobárica
5983,2
8974,8
14958
(b) Calcular W, Q e U para cada processo e para
todo o ciclo.
P(atm)
2.4
A
B
1.2
2.2
360000
0,00831
300
0,0249
120000
300
4,4
2,4
Transformações gasosas
2,4
P (atm)
360000
0,00831
2
1,8
1,6
4,4
1,2
1,4
300
0,0249
57689,9
144,22
1,2
3
4
V (L)
g
b
c
d
e
f
b
c
d
e
f
g
b
c
d
e
f
g
300
0,0249
360000
B -> C: isocórica
A -> B: isobárica
A -> B: isobárica
g
b
c
d
e
f
b
c
d
e
f
g
b
c
d
e
f
g
B -> C: isocórica
Series12
Series15
g
b
c
d
e
f
b
c
d
e
f
g
: compressão
C -> A: isotérmica
900
Diagrama PV
300.000
P (Pa)
V(L)
2,2
360000
a -> b:
isobárica
a -> b:
adiabát
ica
:expans
ão
4.4
 Solução
0,00831
a -> b:
isotérm
ica:
expansã
o
16
C
Tf (K)
Pf (Pa)
Vf(m³)
Ti (K)
Pi (Pa)
Energia
Interna (J)
Vi(m³)
Trabalho
(J)
Estado
Etapa
200.000
Energia
Interna
(atm.L)
Etapa
Trabalho
(atm.L)
Calor
(atm.L)
A -> B: isobárica
5,28
7,92
13,2
B -> C: isocórica
0
-7,92
-7,92
C -> A:
isotérmica:
compressão
-3,6597
0
-3,65979
Ciclo
1,62020
0
1,62020
100.000
0,01
g
b
c
d
e
f
b
c
d
e
f
g
b
c
d
e
f
g
b
c
d
e
f
g
0,012
0,014
0,016
0,018
V (m³)
Series2
: expansão
a -> b: adiabática :expansão
a -> b: isobárica
g
b
c
d
e
f
b
c
d
e
f
g
b
c
d
e
f
g
b
c
d
e
f
g
0,02
0,022
0,024
Series3
a -> b: isobárica
a -> b: isotérmica
a -> b: adiabática
Exemplo 12 - Um sistema constituído por 0,32 mol
de gás ideal monoatômico, cm cv = 3R/2, ocupa um volume
de 2,2 L sob a pressão de 2,4 atm, no estado do ponto A da
figura.
O sistema efetua um ciclo constituído por 3
processos:
(i) O gás é aquecido isobaricamente até atingir o
volume de 4,4 L n ponto B.
(ii) O gás é então resfriado isocoricamente até a
pressão se reduzir a 1,2 atm (Ponto C).
(iii) O gás retorna ao ponto A por meio de uma
compressão isotérmica.
Estado
Vi
(L)
Pi
(atm)
Ti
(K)
Vf
Pf
(L) (atm)
Tf
(K)
A -> B: isobárica
2,2
2,4
201,2 4,4
2,4
402,43
B -> C: isocórica
4,4
2,4
402,4 4,4
1,2
201,2
C -> A: isotérmica:
compressão
4,39
1,2
201,2 2,2 2,399
201,2
16
Resumo e Exemplos Resolvidos – Processos Termodinâmicos - Física – Prof. Dr. Cláudio S. Sartori
17
17