Unidade II
ESTATÍSTICA BASICA
Profa. Maria Ester Domingues de Oliveira
Tabela – Representação Gráfica
Gráfico de Barras
M
éd
io
E
d.
de
E
ns
in
o
E
ns
in
o
E
d.
In
fa
nt
il
Fu
nd
am
en
ta
35
30
25
20
15
10
5
0
E
d.
E
sp
ec
Jo
ia
ve
l
ns
e
A
du
lto
E
d.
P
ro
fis
si
on
al
Número de Matrículas de Educação Básica no Brasil,
por Etapas e Modalidade de Ensino, segundo a região
Geográfica em 29/03/2006.
( emmilh
hõesdealunos)
númerodepessoasmatrículadas
Gráfico de Barras
modalidade de ensino
Diagrama de Pareto
Diagrama de Pareto
Gráfico de Setores
Total (100% - 360 graus)
Gráfico de Setores
Histograma
Ponto médio (1º intervalo): 750
Ponto médio (2º intervalo): 1250
Amplitude do intervalo: 1250 – 750 = 500
Amplitude de meio intervalo: 500/2 = 250
1º intervalo:
Limite inferior: 750 – 250 = 500
Limite superior: 750 + 250 = 1000
Polígono de Freqüências
Histograma e Polígono de
Freqüências
Interatividade
a) 150
b) 200
c)300
d)250
e)nda
Medidas de Tendência Central
As três medidas de tendência central mais
usadas são :
Média
Mediana
Moda
Média
Média
Média
Média
Média
Média
Interatividade
a)112 reais
b)115 reais
c)99 reais
d)114,5 reais
e)nda
Resposta
B) 115 Reais.
_
98+104+120+140+112+80+112+132+135+117
X=
10
_
X = 115
Mediana
A mediana divide um conjunto ordenado
de dados em duas partes com igual
número de elementos.
Se a amostra é constituída por um
número ímpar de elementos
elementos, a mediana é
o valor que fica no centro dos dados
ordenados.
Se a amostra é constituída por um
número par de elementos, a mediana é a
média aritmética dos dois valores
centrais dos dados ordenados.
Mediana
Mediana
Média e Mediana
Moda
A moda de um conjunto de dados é o
valor que ocorre com maior freqüência.
9
9
9
9
9
Um conjunto de dados pode ser:
Amodal
Modal
Bimodal
Trimodal
Polimodal
Moda
Interatividade
e)nda
Resposta
A) moda: 112 reais e mediana: 114,5
reais.
X
98
104
120
140
112
80
132
135
117
f
1
1
1
1
2
1
1
1
1
80 98 104 112 112 117 120 132 135 140
Md = 112 +117
2
= 114,5
Medidas de Dispersão
As medidas de dispersão indicam o
quanto os dados variam em torno da
região central.
São medidas de dispersão:
Amplitude.
Variância.
Desvio padrão
Desvio-padrão.
Coeficiente de Variação.
Variância e Desvio-padrão.
Amplitude e Coeficiente de Variação.
A amplitude é a diferença entre o maior e
o menor dado observado.
Exemplo: No conjunto de dados: 2,
2 5,
5 6,
6 9,
9
10, 10, 12, 15, 18, 20, a amplitude é:
20-2=18.
Exemplo
S2 =
∑( x − x )
n −1
2
Exemplo
Exemplo
Distribuição de Freqüências.
Variância
Exemplo
Exemplo
Exemplo
Fórmulas
PM = (LI +LS) / 2
∑ ( x. f )
⎯χ =
S2 =
S=
CV =
n
∑ (x − x)
2
f
n −1
S
S
X
2
x 100
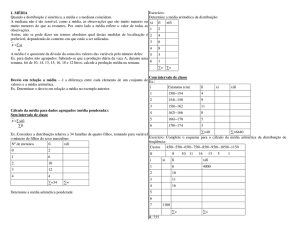
Exercício Resolvido.
Cálculo da média
Calculando a Variância
Calculando a Variância
Comprimento
(em cm)
PM
(xi)
Nº
de
placas
xi.fi
(xi- x)
20
30
25
30
750
25- 49,75=-24,75
30
40
35
45
1575
35- 49,75=-14,75
40
50
45
50
2250
45- 49,75=-4,75
50
60
55
15
825
55- 49,75=5,25
60
70
65
20
1300
65- 49,75=15,25
70
80
75
15
1125
75 49,75=25,25
7549 75=25 25
80
90
85
25
2125
65- 49,75=35,25
200
9950
Total
Calculando a Variância
Comprimento
(em cm)
PM
(xi)
Nº
de
placas
xi.fi
(xi- x)
20
30
25
30
750
-24,75
30
40
35
45
1575
-14,75
40
50
45
50
2250
-4,75
50
60
55
15
825
5,25
60
70
65
20
1300
15,25
70
80
75
15
1125
25 25
25,25
80
90
85
25
2125
35,25
200
9950
Total
Calculando a Variância
Comprimento
(em cm)
PM
(xi)
N de
placas
xi.fi
(xi- x)
(xi- x)2
(f)
20
30
25
30
750
-24,75
(-24,75)2=612,56
30
40
35
45
1575
-14,75
14 75
(-14,75)2 =217,56
40
50
45
50
2250
-4,75
(-4,75)2 =22,56
50
60
55
15
825
5,25
(5,25)2 =27,56
60
70
65
20
1300
15,25
(15,25)2 =232,56
70
80
75
15
1125
25,25
(25 25)2 =637,56
(25,25)
=637 56
80
90
85
25
2125
35,25
35,252 =1242,56
200
9950
Total
Cálculo da Variância
Calculando o Desvio Padrão e
Coeficiente de Variação
S=
CV =
S
S
X
2
x 100
Exemplo.
A partir da tabela abaixo, calcule o valor do desvio padrão
Classes de Salários
(em reais)
Número de
funcionários
800
1000
15
1000
1200
25
1200
1400
5
1400
1600
20
1600
2800
25
1800
2000
10
∑ f= 100
Calculando a média
Salários
PM
(xi)
(f)
xi.fi
800
1000
900
15
13500
1000
1200
1100
25
27500
1200
1400
1300
5
6500
1400
1600
1500
20
30000
1600
1800
1700
25
42500
2000
2200
1900
10
19000
Σf=
f 100
139000
Total
⎯χ =
∑ ( x. f )
n
(xi- x)
(xi- x)2
∑x .f
⎯χ =
∑(139000)
100
= 1390
Calculando a Variância
Salários
PM
(xi)
(f)
xi.fi
(xi- x)
(xi- x)2
800
1000
900
15
13500
-490
240100
1000
1200
1100
25
27500
-290
290
84100
1200
1400
1300
5
6500
-90
8100
1400
1600
1500
20
30000
110
12100
1600
1800
1700
25
42500
310
96100
2000
2200
1900
10
19000
510
260100
Total
Σf= 100
Calculando a Variância
Salários
PM
(xi)
(f)
xi.fi
(xi- x)
(xi- x)2
(xi- x)2.f
800
1000
900
15
13500
-490
240100
3601500
1000
1200
1100
25
27500
-290
84100
2102500
1200
1400
1300
5
6500
-90
8100
40500
1400
1600
1500
20
30000
110
12100
242000
1600
1800
1700
25
42500
310
96100
2402500
2000
2200
1900
10
19000
510
260100
2601000
Total
Σf= 100
Calculando o Desvio padrão
S2
S2
=
∑ (x − x)
2
f
n −1
10990000
=
99
2
S=
S
S=
111.010,101
S = 333,18
= 111.010,101
Interatividade
e)nda
Resposta
a) 18,25 reais.
ATÉ
É A PRÓXIMA!
Ó