1 Exemplos - portuganoia

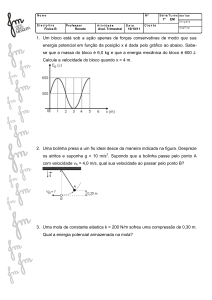
Figura 1.1: Diagrama esquemático ilustrando o sistema do problema.
1
Exemplos
1.1
Um bloco, preso firmemente a uma mola, oscila verticalmente uma frequência de 4 Hertz e uma amplitude
de 7 centímetros. Uma bolinha é colocada em cima do
bloco oscilante assim que chega ao ponto mais baixo
de sua trajetória. Suponha que a massa da bolinha
seja tão pequena que seu efeito sobre o movimento
do bloco seja desprezível. Para qual deslocamento, a
partir da posição de equilíbrio, a bolinha deve perder
contato com um bloco?
Um diagrama esquemático modelando o sistema é exibido na Figura 1.1.
Para resolver esse problema, é preciso considerar que a força elástica da
mola, por ser proporcional ao elongamento, vai decrescendo conforme o sistema
massa mola suba em direção à posição de equilíbrio. É razoável esperar que em
certa etapa desse movimento, a força da mola se torne suficientemente pequena
para produzir o efeito a ser calculado. A primeira etapa dessa solução consiste
em fazer análise das forças através de um diagrama de Corpo Livre aplicado a
sistema massa mola mais a bolinha. Isso está ilustrado na Figura 1.2.
A aplicação da SLN a bolinha gera
N = mg.
(1.1)
No bloco, a a aplicação da SLN na direção y gera a igualdade
−N − M g + kx = 0.
(1.2)
Inserindo o resultado expresso na Equação 1.1 na Equação 1.2, deduz-se que:
(m + M ) g = kx.
1
Figura 1.2: Diagrama de corpo livre da bolinha e da massa.
2
Como M m, M + m ≈ M , e assim,
M g = kx.
Por fim, resolve-se para x:
x=
Mg
.
k
É evidente que a solução passa pela determinação da constante k. Mas isso
pode ser feito aplicando se o resultado extraído da solução da equação diferencial
k
, conclui-se que k = ω 2 M , e
do movimento harmônico simples: como ω 2 = M
como ω = 2πf , então,
x
=
=
=
Mg
ω2 M
g
2
(2πf )
9.8m/s2
2
[2π (4s−1 )]
≈ 1.55cm.
Percebam que esse é o elongamento que a mola terá quando a bolinha perder
contato com a massa. Em relação à posição mínima x = 7cm, a posição será
y ≈ (7 − 1.55) cm = 5.45cm.
1.2
É frequente que especificações militares exigiam que
instrumentos eletrônicos sejam capazes de suportar federações de até 10g. Para se certificar de que os produtos de sua companhia atendam a essa especificação,
seu gerente o instrui a utilizar uma mesa vibratória
que pode fazer comprar um produto com frequências
e amplitudes ajustáveis e controladas. Se um equipamento é colocado sobre a mesa e posto a oscilar com
amplitude de 1,5 centímetros, qual é a frequência que
você deve estar para testar a concordância com as especificações militares?
Para resolvermos esse problema será necessário determinar a velocidade e aceleração de um movimento de oscilação simples.
A velocidade é dada pela derivada da posição em relação ao tempo:
v=
dx
d
=
[xm cos (ωt + φ)]
dt
dt
= xm [− sin (ωt + φ)] ω
= −ωxm sin (ωt + φ) .
3
Já a aceleração é dada pela derivada da velocidade em relação ao tempo:
dv
dt
d
= [−ωxm sin (ωt + φ)]
dt
= [−ωxm cos (ωt + φ)] ω
a=
= − ω 2 xm cos (ωt + φ) .
O valor máximo de aceleração que esse sistema vai suportar corresponde ao
valor máximo da função cosseno. Mas o cosseno é uma função que oscila dentre
os valores -1 e +1. Portanto; o valor máximo de aceleração será dado por
am = ω 2 xm .
Daí, basta relacionar ω e T e usar o valor de xm fornecido no enunciado:
am = 10g = ω 2 xm
2
⇒10g = (2πf ) xm
2
⇒ (2πf ) xm = 10g
10g
2
⇒ (2πf ) =
x
r m
10g
⇒2πf =
xm
q
⇒f =
⇒f =
10g
xm
q2π
10(9.8m/s2 )
1.5×10−2 m
2π
= 1.29 × 101 s−1
= 1.29 × 101 Hz.
1.3
Um cabo de guindaste possui uma área de seção reta
de 1,5 centímetro quadrado de um comprimento de 2,5
metros. O módulo de Young do cabo é de 150GN/m2 .
Um bloco de motor de 950 quilogramas é pendurado
na extremidade do Cabo. (a) de quanto se distende o
cabo? (b) o cabo foi tratado como uma mola simples
Qual é a frequência de oscilação do bloco de motor
extremidade do Cabo?
Esse é um problema que vai demandar a aplicação do conceito de módulo de
Young E, definido por
∆l
F
=E .
A
l
4
A distenção ∆l é dada então por
Fl
AE
M gl
=
AE
(950kg) 9.8m/s2 (2.5m)
=
(1.5 × 10−4 m2 ) 150 × 109 mN2
∆l =
= 1.03 × 10−3 m
= 1.03mm.
Para substituir esse sistema por um sistema massa mola, basta considerar que,
quando sujeito a uma força correspondente ao peso do bloco de motor, o elongamento é x = 1.03mm.
Isso permite a determinação da constante k:
F = kx
⇒M g = kx
⇒kx = M g
Mg
⇒k =
x
(950kg) 9.8m/s2
=
1.03 × 10−3 m
= 9.04 × 106 N/m.
Com tal constante, a frequência será dada por
f=
⇒f =
⇒f =
ω
2π
q
k
M
2π
q
9.04×106 N/m
950kg
2π
= 1.55 × 101 s−1
= 1.55 × 101 Hz.
5
Figura 1.3: Edifício Taipei 101 a esquerda, e a massa do amortecedor, estimada
em torno de 728 toneladas.
1.4
Fortes ventos são capazes de produzir oscilações em
prédios altos (http://sofisica.com.br/conteudos/Ondulatoria/
MHS/movpereosc2.php, http://www.cesec.ufpr.br/etools/
oe3/applets/forca_vento/). Por exemplo, o Taipei 101
é um dos maiores prédios do mundo, e conta com
amortecedor especialmente desenhado para absorver
essas influências externas (veja a Figura 1.3). Imagine
que as oscilações durem 1s. Sabendo disso, determine
o valor da constante das molas usadas no amortecedor, e qual deve ser a amplitude de oscilação do prédio todo, que tem uma massa total aproximada em
700.000 toneladas.
Para resolver esse problema, será necessário fazer uma série de hipóteses e aproximações que vão simplificá-lo.
A primeira hipótese a ser feita é que o período da oscilação não seja afetado
pelo uso do amortecedor, então, continuaria a ser um segundo. É bastante
realista se for considerando que a massa do amortecedor (728 toneladas) é muito
menor que a massa do prédio (700000 toneladas). Se for assim, a expressão
r
r
1
1
M +m
M
0
T =
≈
=T
2π
k
2π
k
mostra que se a massa do amortecedor for pequena se comparada com a do
prédio, o período se manterá inalterado.
Vejamos qual deve ser a constante das molas.
É de se esperar, visando manter o sistema estável, que seja utilizado na
verdade um par de molas conforme ilustrado na Figura 1.4.
Deve se notar que as expressões deduzidas do estudo do oscilador harmônico
envolvem apenas uma mola, de forma que a presença de duas molas introduz
uma complexidade a ser resolvida. Para contorná-la, será aplicado o conceito
de mola equivalente. Uma uma mola será equivalente a esse par de molas se,
sujeita ao mesmo elongamento, produza a mesma força.
6
Figura 1.4: Diagrama esquemático do sistema simplificado.
O elongamento sofrido por uma das molas tem que corresponder a compressão da outra. Isso está ilustrado na Figura 1.5.
A aplicação da SLN na massa produz a equação
FRes = F1 + F2 = k1 x + k2 x.
Como essa deve ser a força produzida pela mola equivalente:
k1 x + k2 x = keq x,
conclui-se que keq = k1 + k2 .
Se as duas molas forem iguais, k1 = k2 e a mola equivalente terá uma
constante que será o dobro de cada uma delas.
Então, esse é o plano: resolver o problema com a mola equivalente, e então
dividi-la por 2 para obter a constante de cada uma dessas molas.
Sendo assim, do período T = 1s, deduz-se keq . Como ω = 2πf , segue que
ω = 2π
T , e daí,
s
2π
M
2π
= q = 2π
T =
ω
keq
k
M
M
⇒T 2 = 4π 2
keq
T2
M
=
2
4π
keq
2
⇒keq T = M 4π 2
⇒
4π 2 M
T2
2
4π 728 × 103 kg
⇒keq =
=
(1s)
2
= 2.9 × 107 N/m.
Logo, a constante de cada mola será
k=
keq
= 1.4 × 107 N/m.
2
Uma mola bastante dura por sinal.
Agora, vejamos a questão da oscilação do prédio.
A segunda hipótese que faremos será considerar que a força que o vento
imprime ao prédio será transformada numa força interna do sistema pelo amortecedor. Sendo assim, a somatória das forças externas seria nula e portanto a
posição do sistema de massa não seria alterada.
7
Figura 1.5: Diagrama esquemático ilustrando a relação entre a compressão e o
elongamento das duas molas. (a) Situação de equilíbrio. (b) Após um pequeno
deslocamento da massa, a mola a esquerda sofre uma compressão ~x e a mola a
direita um elongamento ~x. Se fossem diferentes, ocorreria o absurdo da posição
extrema da mola a direita ter penetrado na massa, ou da mola a esquerda ter
perdido contato com a ela. (c) A mola equivalente, representada por keq deve
produzir a mesma força que as duas molas conjugadas em série dado o mesmo
deslocamento da massa.
8
Desta forma, se o sistema de referência for centrado no sistema de massa
do sistema, ele não será alterado, e permanecerá nulo após o deslocamento da
massa amortecedora.
A Figura 1.6 ilustra tal situação.
Se o centro de massa permanece em zero, então,
x1 M1 + x2 M2 = 0,
(1.3)
sendo x1 a posição do amortecedor após a oscilação, e x2 a posição do prédio
correspondente.
Para determinar x1 , pesquisei na rede qual pode ser a força transmitida pelos
ventos, que é da ordem de 22680N. Se ela for transformada completamente em
uma força interna, a mola deverá imprimir essa força ao amortecedor:
F = keq x1 .
Daí, a amplitude dessa oscilação será
x1 =
22680N
F
= 1.6 × 10−3 m.
=
keq
1.4 × 107 N/m
Fazendo referência à Figura 1.3, verifica se que tal deslocamento se dá no
sentido negativo ao do eixo x e portanto será considerado um valor negativo:
x1 = −1.6 × 10−3 m.
Bom, mas sendo assim, a amplitude da oscilação do prédio será determinada
pela equação 1.3:
x 1 M1 + x 2 M 2 = 0
⇒x2 M2 = −x1 M1
x 1 M1
⇒x2 = −
M2
−1.6 × 10−3 m 728 × 103 kg
=−
7.0 × 107 kg
−5
≈ 1.6 × 10 m = 16µm.
Um resultado excelente!
Mas, muito cuidado!
A hipótese de que a força exercida pelo vento seja convertida totalmente na
força da mola no amortecedor é ingênua!
Muito provavelmente, há outros mecanismos internos que concorrem com a
força da mola, e além disso, há outras formas de se tratar esse tipo de fenômeno
como por exemplo o que se vê quando se estuda um módulo de compressão de
Young.
Então, certamente, há formas mais adequadas de se tratar esse problema.
Não obstante, esse exemplo mostra como problemas complexos são tratados:
são usadas hipóteses simples, refinadas com hipóteses corrigidas e aprimoradas.
9
Figura 1.6: Diagrama esquemático ilustrando que a posição do centro de massa
se manterá inalterada durante uma oscilação do sistema prédio + amortecedor.
10