01 - (ITA SP/2011) Um problema clássico da cinemática considera

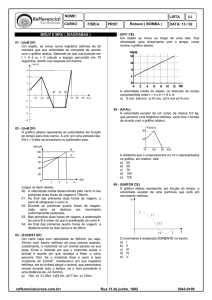
01 - (ITA SP/2011)
Um problema clássico da cinemática considera
objetos que, a partir de certo instante, se movem
conjuntamente com velocidade de módulo
constante a partir dos vértices de um polígono
regular, cada qual apontando à posição
instantânea do objeto vizinho em movimento. A
figura mostra a configuração desse movimento
múltiplo no caso de um hexágono regular.
Considere que o hexágono tinha 10,0 m de lado
no instante inicial e que os objetos se
movimentam com velocidade de módulo
constante de 2,00 m/s. Após quanto tempo estes
se encontrarão e qual deverá ser a distância
percorrida por cada um dos seis objetos?
a)
b)
c)
d)
e)
5,8 s e 11,5 m
11,5 s e 5,8 m
10,0 s e 20,0 m
20,0 s e 10,0 m
20,0 s e 40,0 m
Gab: C
02 - (ITA SP/2009)
Na figura, um ciclista percorre o trecho AB com
velocidade escalar média de 22,5 km/h e, em
seguida, o trecho BC de 3,00 km de extensão. No
retorno, ao passar em B, verifica ser de 20,0 km/h
sua velocidade escalar média no percurso então
percorrido, ABCB. Finalmente, ele chega em A
perfazendo todo o percurso de ida e volta em 1,00
h, com velocidade escalar média de 24,0 km/h.
Assinale o módulo v do vetor velocidade média
referente ao percurso ABCB.
Gab: A
03 - (ITA SP/2007)
A figura mostra uma pista de corrida A B C D E F,
com seus trechos retilíneos e circulares
percorridos por um atleta desde o ponto A, de
onde parte do repouso, até a chegada em F, onde
pára. Os trechos BC, CD e DE são percorridos com
a mesma velocidade de módulo constante.
Considere as seguintes afirmações:
I. O movimento do atleta é acelerado nos
trechos AB, BC, DE e EF.
II. O sentido da aceleração vetorial média do
movimento do atleta é o mesmo nos trechos
AB e EF.
III. O sentido da aceleração vetorial média do
movimento do atleta é para sudeste no trecho
BC, e, para sudoeste, no DE.
Então, está(ão) correta(s)
a) apenas a I.
b) apenas a I e II.
c) apenas a I e III.
d) apenas a II e III.
e) todas.
Gab: E
04 - (ITA SP/2009)
Dentro de um elevador em queda livre num
campo gravitacional g, uma bola é jogada para
baixo com velocidade v de uma altura h. Assinale
o tempo previsto para a bola atingir o piso do
elevador.
a) t  v / g
b) t  h / v
a)
b)
c)
d)
e)
v = 12, 0 km/h
v = 12, 00 km/h
v = 20, 0 km/h
v = 20, 00 km/h
v = 36, 0 km/h
c)
t  2h / g
d)
t  ( v 2  2 gh  v ) / g
e)
t  ( v 2  2 gh  v ) / g
Gab: B
c)
05 - (ITA SP/2009)
Um barco leva 10 horas para subir e 4 horas para
descer um mesmo trecho do rio Amazonas,
mantendo constante o módulo de sua velocidade
em relação à água. Quanto tempo o barco leva
para descer esse trecho com os motores
desligados?
a)
b)
c)
d)
e)
14 horas e 30 minutos
13 horas e 20 minutos
7 horas e 20 minutos
10 horas
Não é possível resolver porque não foi dada a
distância percorrida pelo barco.
Gab: B
06 - (ITA SP/2001)
Uma partícula descreve um movimento cujas
coordenadas são dadas pelas seguintes
equações:
X(t) = X0 cos(w t) e Y(t) = Y0 sen (w t + /6), em
que w, X0 e Y0 são constantes positivas. A
trajetória da partícula é
a) Uma circunferência percorrida no sentido
anti-horário
b) Uma circunferência percorrida no sentido
horário.
c) Uma elipse percorrida no sentido antihorário.
d) Uma elipse percorrida no sentido horário.
e) Um segmento de reta.
Gab: C
07 - (ITA SP/2001)
Uma partícula, partindo do repouso, percorre no
intervalo de tempo t, uma distância D. Nos
intervalos de tempo seguintes, todos iguais a t,
as respectivas distâncias percorridas são iguais a
3D, 5D, 7D etc. A respeito desse movimento
pode-se afirmar que
a) a distância da partícula desde o ponto em
que inicia seu movimento cresce
exponencialmente com o tempo.
b) a
velocidade
da
partícula
cresce
exponencialmente com o tempo.
d)
e)
a distância da partícula desde o ponto em
que inicia seu movimento é diretamente
proporcional ao tempo elevado ao
quadradp.
a velocidade da partícula é diretamente
proporcional ao tempo elevado ao
quadrado.
nenhuma das opções acima está correta.
Gab: C
08 - (ITA SP/2005)
Um avião de vigilância aérea está voando a uma
altura de 5,0 km, com velocidade de 50 10 m/s no
rumo norte, e capta no radiogoniômetro um sinal
de socorro vindo da direção noroeste, de um
ponto fixo no solo. O piloto então liga o sistema
de pós-combustão da turbina, imprimindo uma
aceleração constante de 6,0 m/s2. Após 40 10 / 3s ,
mantendo a mesma direção, ele agora constata
que o sinal está chegando da direção oeste. Neste
instante, em relação ao avião, o transmissor do
sinal se encontra a uma distância de:
a) 5,2 km
b) 6,7 km
c) 12 km
d) 13 km
e) 28 km
Gab: D
09 - (ITA SP/2002)
Billy sonha que embarcou em uma nave espacial
para viajar até o distante planeta Gama, situado a
10,0 anos-luz da Terra. Metade do percurso é
percorrida com aceleração de 15 m/s2, e o
restante com desaceleração de mesma
magnitude. Desprezando a atração gravitacional e
efeitos relativistas, estime o tempo total em
meses de ida e volta da viagem do sonho de Billy.
Justifique detalhadamente.
Gab: 10 anos ou 120 meses
10 - (ITA SP/2011)
Um exercício sobre a dinâmica da partícula tem
seu início assim enunciado : Uma partícula está
se movendo com uma aceleração cujo módulo é
dado por (r + a3/r2) , sendo r a distância entre a
origem e a partícula. Considere que a partícula foi
lançada a partir de uma distância a com uma
velocidade inicial
2 a .
Existe algum erro
pedra também leva para atingir o solo, após ser
lançada para cima até uma altura h, como mostra
a figura.
conceitual nesse enunciado ? Por que razão?
a)
b)
Não, porque a expressão para a velocidade é
consistente com a da aceleração;
Sim, porque a expressão correta para a
velocidade seria 2a 2  ;
c)
Sim, porque a expressão correta para a
velocidade seria 2a 2  / r ;
d)
Sim, porque a expressão correta para a
velocidade seria
e)
2 a 2 / r
Assinale e expressão que dá a altura H.
;
Sim, porque a expressão correta para a
velocidade seria 2a  ;
Gab: E
a)
b) H 
c)
11 - (ITA SP/2007)
Equipado com um dispositivo a jato, o homemfoguete da figura cai livremente do alto de um
edifício até uma altura h, onde o dispositivo a jato
é acionado. Considere que o dispositivo forneça
uma força vertical para cima de intensidade
constante F. Determine a altura h para que o
homem pouse no solo com velocidade nula.
Expresse sua resposta como função da altura H,
da força F, da massa m do sistema homemfoguete e da aceleração da gravidade g,
desprezando a resistência do ar e a alteração da
massa m no acionamento do dispositivo.
H
H
d) H 
e) H 
t12 t 2 2 h
2(t 22 - t12 ) 2
t1 t 2 h
4(t 22 - t12
2 t12 t 22 h
(t 22 - t12 ) 2
4 t1 t 2 h
( t 22 - t12 )
4 t12 t 22 h
( t 22 - t12 ) 2
Gab: E
13 - (ITA SP/2003)
A partir do repouso, uma pedra é deixada cair da
borda no alto de um edifício. A figura mostra a
disposição das janelas, com as pertinentes alturas
h e distâncias L que se repetem igualmente para
as demais janelas, até o térreo. Se a pedra
percorre a altura h da primeira janela em t
segundos, quanto tempo levará para percorrer,
em segundos, a mesma altura h da quarta janela?
(Despreze a resistência do ar).
p ed ra
L
Gab:
h
1 ª ja n e la
h
2 ª ja n e la
L
mgH
F
12 - (ITA SP/2006)
À borda de um precipício de um certo planeta, no
qual se pode desprezar a resistência do ar, um
astronauta mede o tempo t1 que uma pedra leva
para atingir o solo, após deixada cair de uma
altura H. A seguir, ele mede o tempo t2 que uma
h
L
a)
[( L  h  L ) / ( 2L  2h  2L  h )]t
b) [( 2L  2h)  2L  h ) / ( L  h  L )]t
c)
[( 4(L  h)  3(L  h)  L ) / ( L  h  L )]t
d) [( 4(L  h)  3(L  h)  L ) / ( 2L  2h  2L  h )]t
e) [( 3(L  h)  2(L  h)  L ) / ( L  h  L )]t
Gab: C
14 - (ITA SP/2001)
Em um farol de sinalização, o feixe de luz está
acoplado a um mecanismo rotativo que realiza
uma volta completa a cada T segundos. O farol se
encontra a uma distância R do centro de uma
praia de comprimento 2L, conforme a figura. O
tmepo necessário para o feixe de luz “varrer” a
praia, em cada volta, é
Farol
R
L
16 - (ITA SP/2001)
No sistema convencional de tração de bicicletas, o
ciclista impede os pedais, cujo eixo movimenta a
roda dentada (coroa) a ele solidária. Esta, por sua
vez, aciona a corrente responsável pela
transmissão do movimento a outra roda dentada
(catraca), acoplada ao eixo traseiro da bicicleta.
Considere agora um sistema duplo de tração, com
2 coroas, de raios R1 e R2 (R1<R2) e 2 catracas R3 e
R4 (R3<R4), respectivamente. Obviamente, a
corrente só toca uma coroa e uma catraca de cada
vez, conforme o comando da alavanca de câmbio.
A combinação que permite máxima velocidade da
bicicleta, para uma velocidade angular dos pedais
fixa, é
a) coroa R1 e catraca R3
b) coroa R1 e catraca R4
c) coroa R2 e catraca R3
d) coroa R2 e catraca R4
e) é indeterminada já que não se conhece o
diâmetro da roda traseira da bicicleta.
L
Gab: C
a)
b)
c)
d)
e)
arctg(L/R) T/(2)
arctg(2L/R) T/(2)
arctg(L/R) T/
arctg(L/2R) T/(2)
arctg(L/R) T/
Gab: C/E
15 - (ITA SP/2001)
Uma partícula move-se ao longo de uma
circunferência circunscrita em um quadrado de
lado L com velocidade angular constante. Na
circunferência inscrita nesse mesmo quadrado,
outra partícula move-se com a mesma velocidade
angular. A razão entre os módulos das respectivas
velocidades tangenciais dessas partículas é
a)
a)
b)
c)
d)
e)
p2 = 9p1.
p2 = 9p1/4.
p2 = 9p1/7.
p2 = 15p1/7.
p2 = −15p1/7.
Gab: A
2
b) 2 2
c)
2
2
d)
3
2
e)
3
2
Gab: A
17 - (ITA SP/2009)
Um espelho esférico convexo reflete uma imagem
equivalente a 3/4 da altura de um objeto dele
situado a uma distância p1. Então, para que essa
imagem seja refletida com apenas 1/4 da sua
altura, o objeto deverá se situar a uma distância
p2 do espelho, dada por
18 - (ITA SP/2002)
Um ginásio de esportes foi projetado na forma de
uma cúpula com raio de curvatura R = 39,0m,
apoiada sobre uma parede lateral cilíndrica de
raio y = 25,0m e altura h = 10,0m, como mostrado
na figura. A cúpula comporta-se como um espelho
esférico de distância focal f = R/2 , refletindo
ondas sonoras, sendo seu topo o vértice do
espelho. Determine a posição do foco relativa ao
piso do ginásio. Discuta, em termos físicos as
consequências
práticas
deste
projeto
arquitetônico.
pequenos, a distância
adjacentes do CD é de:
entre
duas
trilhas
h
R
//////////////
Considerando nas duas situações 1 e 2 ângulos
.
//////////////
y
Gab: 0,4m
19 - (ITA SP/2007)
Um raio de luz de uma lanterna acesa em A
ilumina o ponto B, ao ser refletido por um espelho
horizontal sobre a semi-reta DE da figura, estando
todos os pontos num mesmo plano vertical.
Determine a distância entre a imagem virtual da
lanterna A e o ponto B.
Considere AD 2 m , BE  3 m e DE  5 m .
Gab: A' B  7,1m
20 - (ITA SP/2006)
Para se determinar o espaçamento entre duas
trilhas adjacentes de um CD, foram montados dois
arranjos:
1. O arranjo da figura (1), usando uma rede de
difração de 300 linhas por mm, um LASER e
um anteparo. Neste arranjo, mediuse a
distância do máximo de ordem 0 ao máximo
de ordem 1 da figura de interferência formada
no anteparo.
2. O arranjo da figura (2), usando o mesmo
LASER, o CD e um anteparo com um orifício
para a passagem do feixe de luz. Neste
arranjo, mediuse também a distância do
máximo de ordem 0 ao máximo de ordem 1
da figura de interferência.
a)
b)
c)
d)
e)
2,7 x 107 m
3,0 x 107 m
7,4 x 106 m
1,5 x 106 m
3,7 x 105 m
Gab: D
21 - (ITA SP/2004)
Ao olhar-se num espelho plano, retangular, fixado
no plano de uma parede vertical, um homem
observa a imagem de sua face tangenciando as
quatro bordas do espelho, isto é, a imagem de sua
face encontra-se ajustada ao tamanho do
espelho. A seguir, o homem afasta-se,
perpendicularmente à parede, numa certa
velocidade em relação ao espelho, continuando a
observar sua imagem. Nestas condições, pode-se
afirmar que essa imagem
a) torna-se menor que o tamanho do espelho tal
como visto pelo homem.
b) torna-se maior que o tamanho do espelho tal
como visto pelo homem.
c) continua ajustada ao tamanho do espelho tal
como visto pelo homem.
d) desloca-se com o dobro da velocidade do
homem.
e) desloca-se com metade da velocidade do
homem.
Gab: C