CAPÍTULO IV - POSIÇÕES RELATIVAS DE UMA RETA E UM

CAPÍTULO IV - POSIÇÕES RELATIVAS
DE UMA RETA E UM PLANO
E
DE DUAS RETAS
4.1 Posições relativas de uma reta e um plano
r
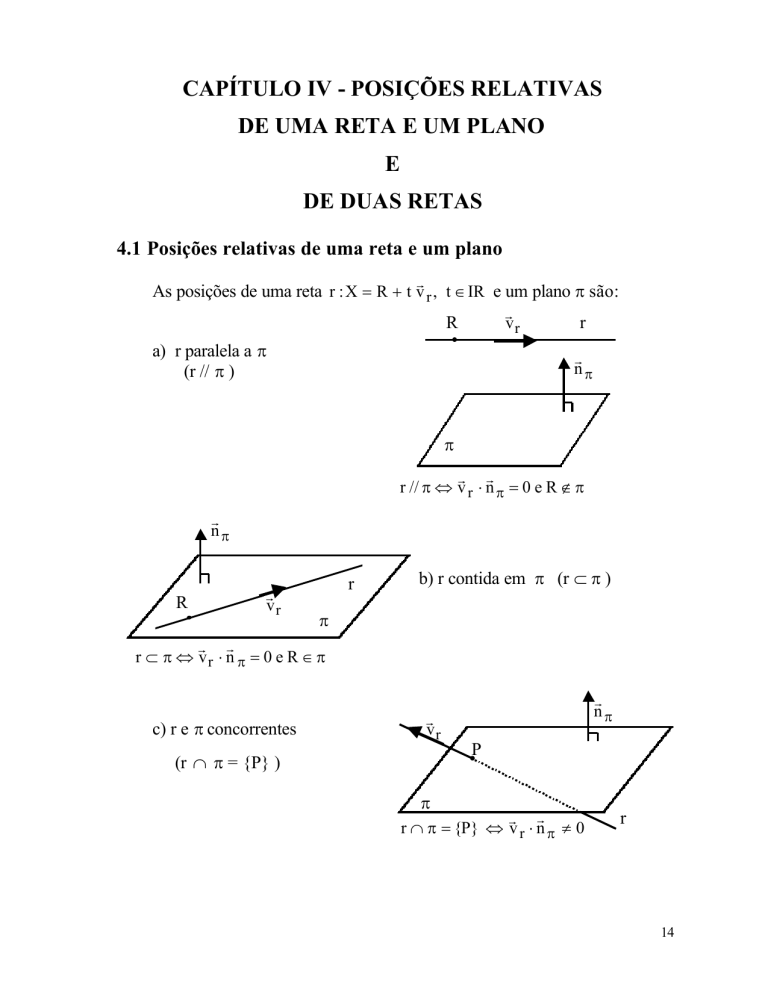
As posições de uma reta r : X = R + t v r , t ∈ IR e um plano π são:
r
vr
R
a) r paralela a π
(r // π )
r
r
nπ
π
r r
r // π ⇔ v r ⋅ n π = 0 e R ∉ π
r
nπ
R
r
vr
r
b) r contida em π (r ⊂ π )
π
r r
r ⊂ π ⇔ vr ⋅ n π = 0 e R ∈ π
c) r e π concorrentes
r
nπ
r
vr
P
(r ∩ π = {P} )
π
r r
r ∩ π = {P} ⇔ v r ⋅ n π ≠ 0
r
14
Caso particular:
r
vr
v
nπ
π
r
Exemplos:
1. Determine a interseção da reta r com o plano π, nos seguintes casos:
a) r : X = (1,6,2) + t (1,1,1) ; t ∈ IR
π: x − z − 3 = 0
b) r : x − 1 = y − 2 = 2 (z − 1)
π : X = h(6,2,1) + t (1,2,1); t, h ∈ IR
x = t

c) r :  y = −3 + 3 t ; t ∈ IR
z = −t

π : x + y + 2z − 1 = 0
Solução:
r
r
a) v r ⋅ n π = (1,1,1) ⋅ (1,0,−1) = 0, logo, r ∩ π = r ou r ∩ π = φ .
Como R(1,6,2) é um ponto de r, verificamos que R ∉ π . Logo r ∩ π = φ .
r
 1 r
b) Sendo v r = 1,1,  e n π = (6,2,1) × (1,2,1) = (0,−5,10), temos que
 2
r r
v r ⋅ n π = 0 . Logo, r ∩ π = r ou r ∩ π = φ . Como R(1,2,1) é um ponto de
r, verificamos que R ∈ π . Logo r ⊂ π e consequentemente r ∩ π = r.
15
r
r
b) De v r ⋅ n π = (1,3,−1) ⋅ (1,1,2) = 2 ≠ 0 concluímos que r e π são
concorrentes. Seja r ∩ π = {P} = {( a, b, c)} . Temos então:
(1) a + b + 2c − 1 = 0.
a = t

(2) b = −3 + 3 t , para algum escalar t .
c = − t

De (1) e (2) obtemos t = 2 e P( 2,3,−2) .
2. Determine uma equação da reta r que passa pelo ponto A(1,0,−2) e é
paralela aos planos α : 2x − y + 2 = 0 e β : x + z − 3 = 0.
Solução:
r
r
r
r
r
r
Como r //α e r // β, temos v r ⊥ n α e v r ⊥ n β . Sendo n α e n β LI,
r
r
r
temos que vr // n α × n β . Assim podemos considerar
r
r
r
vr = n α × n β = (1,01) × (2,−1,0) = (1,2,−1) .
Daí uma equação vetorial da reta r é:
r : X = (1,0, −2) + t (1,2, −1); t ∈ IR
4.2 Posições relativas de duas retas
Se duas retas estão contidas no mesmo plano dizemos que são
coplanares. Caso contrário são denominadas reversas.
As retas coplanares podem ser paralelas (distintas ou coincidentes) ou
concorrentes.
16
Resumindo, duas retas r1 e r2 podem ser:
Coplanares
w Concorrentes : r1 ∩ r2 = {P}
r1
π
P
r2
w Paralelas:
w Distintas : r1
∩ r2 = φ
w Coincidentes : r1
π
r1
≡ r2
π
r1 ≡ r2
r2
Reversas
r1
P
r2
π
Estabeleceremos a seguir condições para a identificação da posição
relativa de duas retas.
r
r
Considere as retas r : X = R + h v r e s : X = S + t v s ; h, t ∈ IR .
→ r
r
Se r e s são coplanares então os vetores RS, v r e vs são coplanares e
→ r r
→ r r
portanto [ RS, v r , vs ] = 0. Reciprocamente, se [ RS, v r , vs ] = 0 podemos
ter:
r
r
i) v r // v s , nesse caso r e s são paralelas, logo coplanares.
17
r
r
ii) v r e v s LI, nesse caso
→ r
r
r
r
RS, vr e vs são LD. Como v r e v s são
→
linearmente independentes, então podemos escrever RS como
r
r
combinação linear de v r e v s . Logo, existem escalares ho e to tais que
r
r
r
r
S = R + h o v r + t o v s . Assim, o plano β : X = R + h v r + t v s ; h, t ∈ IR ,
contém as retas r e s, que portanto são coplanares. Observemos ainda
que, neste caso as retas são concorrentes.
Um caso particular de retas concorrentes
são as retas perpendiculares. Observemos
que se duas retas r e s são perpendiculares
r r
então v r ⋅ v s = 0 .
r
vs
r
vr
r
P
s
π
Exemplos
1. Estude a posição relativa dos seguintes pares de retas:
2x − y − z + 2 = 0
a) r : 
 x + 3y − z + 2 = 0
e s : X = (1,0,2) + h (1,−3,7); h ∈ IR
x = h
1− x y

b) r :  y = 1 − h ; h ∈ IR e s :
= =z−8
2
3
 z = 4 + 4h

x −3
z − 12
= y− 2=
5
9
x = 4

d) r : X = ( 4,−3,1) + h (0,2,1); h ∈ IR e s :  y = −1 − 2t ; t ∈ IR
z = 3 − t

c) r : X = ( −2,1,3) + t ( −10,−2,−18) ; t ∈ IR e s :
Solução:
r
r
a) Como v r // ( 2,−1,−1) × (1,3,−1) = ( 4,1,7 ) e v s // (1,−3,7) temos que as
retas r e s são concorrentes ou reversas. Vamos então considerar
R(0,0,2) e S(1,0,2) pontos de r e s, respectivamente. Assim,
18
1 0 0
r
[ RS, vr , vs ] = 4 1 7 = 28 ≠ 0 .
1 −3 7
→ r
Portanto, as retas r e s são reversas.
r
r
c) Como v r // (1,−1,4) e v s // ( −2,3,1) temos que as retas r e s são
concorrentes ou reversas. Vamos então considerar R(0,1,4) e S(1,0,8)
pontos de r e s, respectivamente.
Assim,
→ r
r
[ RS, v r , vs ] =
1 −1 4
1 − 1 4 = 0 . Logo as retas r e s são concorrentes.
−2 3 1
r
r
c) Como v r // ( −10 ,−2,−18) e v s // (5,1,9) temos que as retas r e s são
paralelas (distintas ou coincidentes). Além disso, o ponto R ( −2,1,3)
pertence às retas r e s. Assim, podemos concluir que as retas r e s são
coincidentes.
r
r
d) Como v r // ( 0,2,1) e v s // (0,− 2,−1) temos que as retas r e s são
paralelas (distintas ou coincidentes). Observemos que o ponto R ( 4,−3,1)
pertence à reta r, no entanto não pertence à reta s, pois o sistema
 4= 4

 − 3 = −1 − 2 t o não tem solução.
 1= 3− t

o
Assim, podemos concluir que as retas r e s são paralelas distintas.
2. Dê uma equação da reta r que passa pelo ponto P( −1,1,1) e é paralela à
 2x − y + 4z + 3 = 0
reta s: 
.
x + 5y − z + 6 = 0
19
Solução:
r
r
s retas paralelas podemos considerar v r = v s . Como
r
v s // (2,− 1,4) × (1,5,−1) = (− 19,6,11) as equações simétricas de s são:
Sendo r
e
x +1 y −1 z −1
=
=
.
− 19
6
11
x = 4 + t

3. Mostre que as retas r : x − 2 = − y = z − 1 e s :  y = −2 − t; t ∈ IR
z = 3

são concorrentes e determine o ponto de interseção.
Solução:
r
r
Sejam v r = (1,−1,1), v s = (1,− 1,0) e R(2,0,1) e S(4, −2,3) pontos de r e
s,
respectivamente.
Então
1 −1 1
r r →
[ v r , vs , RS] = 1 −1 0 = 0
2 −2 2
e
assim
concluímos
r
r
que r e s são coplanares. Como não são paralelas pois v r e v s são
vetores LI, temos que as retas são concorrentes. Seja
{Po } = {( x o , y o , z o )} = r ∩ s .
x o = 4 + t o

Então, x o − 2 = − y o = z o − 1 e  y o = −2 − t o .
z = 3
 o
Daí, t o = 0 e Po = ( 4,−2,3).
4. Determine uma equação da reta r que passa pelo ponto P (1,2,3), é
concorrente com a reta s : X = ( −1,3,5) + h (2,5,1); h ∈ IR, e tem vetor
r
r
direção v r ortogonal ao vetor u = ( 0,1,−4) .
20
Solução:
Seja
{Po } = r ∩ s .
Então
existe
um
real
ho ,
tal
que
→
r
r
Po ( −1 + 2 h o ,3 + 5h o ,5 + h o ) . Consideremos vr = PPo . Como v r é
r
ortogonal a u , temos que ( −2 + 2h o ,1 + 5h o ,2 + h o ) ⋅ (0,1,−4) = 0 . Logo,
h o = 7. Assim,
Po = (13,18,12) e r : X = (1,2,3) + t (2,5,1); t ∈ IR .
5. Determine uma condição necessária e suficiente para que uma reta r
seja paralela ao eixo OX.
Solução:
r
O eixo OX tem vetor direção i = (1,0,0 ). Então, uma reta r é paralela ao
r
r
eixo OX se, e somente se, v r é paralelo ao vetor i = (1,0,0 ).
6. Determine uma equação da reta que passa pelo ponto P = (1,0,2), é
concorrente com a reta s : X = (1,0,1) + t (2,1,1); t ∈ IR e é paralela ao
plano π : 2x − 3y + 4z − 6 = 0 .
Solução:
P0
P
r
Seja
{Po } = r ∩ s
então, existe t ∈ IR tal que
→
Po = (1 + 2t , t ,1 + t ) e PPo = ( 2t , t , t − 1) .
π
s
Como r // π temos ( 2t, t , t − 1) ⋅ ( 2,−3,4) = 0 .
4
Assim, t = .
5
r
Considerando v r = (8,4,−1) , uma equação vetorial de r é:
r : X = (1,0,2) + t (8,4, −1); t ∈ IR .
21