Baixar o arquivo

Aula 4
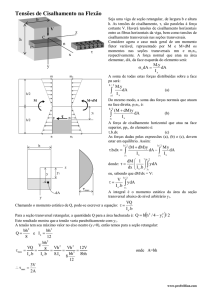
Tensões de Cisalhamento no Regime Elástico
Cisalhamento na flexão
Em elementos estruturais (vigas, eixos e barras) submetidos à ação de esforços
cortantes (cisalhamento) V, surge nas seções transversais destes elementos uma
distribuição de tensão de cisalhamento  não uniforme, quando ela age em conjunto com a
Tensão de Flexão, na qual provoca deformações nas seções transversais, conforme
ilustrado a seguir.
O esforço cortante V GERA
distribuição não uniforme de tensão de cisalhamento .
Fórmula de cisalhamento
Em qualquer seção transversal de um elemento estrutural (vigas, eixos e barras) sob a
ação de um esforço cortante, surge nesta seção transversal uma distribuição de tensão de
cisalhamento não uniforme, conforme ilustrado na figura a seguir:
Considerando que o material do elemento estrutural trabalha no regime elástico, a tensão
de cisalhamento em qualquer ponto p na seção transversal é definida por:
Em que:
 tensão de cisalhamento;
V esforço cortante na seção;
Q = A’. y’ momento estático da área sombreada acima ou abaixo ao nível do ponto p em
análise;
I Momento de inércia da seção transversal relação ao eixo centroidal (C.G.);
t largura da seção ao nível do ponto p em análise.
Para uma viga com seção transversal retangular, a tensão de cisalhamento varia
parabolicamente com a altura, conforme ilustrado na figura anterior.
Analisando a equação acima, observa-se:
A. Pontos localizados no topo e na base da seção transversal possui Q = 0, logo,
a tensão de cisalhamento é nula;
B. Em seções transversais com largura constante a tensão de
cisalhamento máxima ocorre ao longo da linha neutra ou eixo neutro,
conforme ilustra a figura a seguir.
A máxima tensão de cisalhamento para seções de largura constante ocorre ao
nível do centro de gravidade C.G. .
Para seções de largura constante o momento estático Q é máximo ao nível do C.G.
RESULTANDO NA MÁXIMA TENSÃO DE CISALHAMENTO.
C. Para seções com largura que varia ao longo da mesma  Nem sempre a
máxima tensão de cisalhamento ocorre ao nível do centro de gravidade
C.G.
Nestes casos é necessário comparar a tensão ao nível do centro de gravidade C.G.,
com a tensão ao nível da menor largura mais próxima do centro de gravidade C.G, no caso
de existir um nível próximo de menor largura.
Exemplo 01 - ( Exemplo 7.1 Hibbeler): A seção
transversal de uma viga de madeira está sujeita a uma
força de cisalhamento (cortante) vertical interna
resultante V = 3 kN. Determine:
a) A tensão de cisalhamento no ponto p. Represente
o estado de tensão do ponto p desenhando o
resultado
em um elemento infinitesimal de
volume localizado neste ponto;
b) A tensão de cisalhamento máxima que ocorre na
seção.
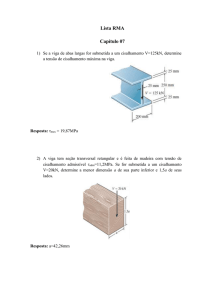
Exemplo 02 - Uma viga de aço tem as mesmas dimensões mostradas na figura a seguir.
Se for submetida a uma força de cisalhamento (cortante) V = 80 kN, determine para cada
caso:
a) a tensão de cisalhamento no ponto p. Represente o estado de tensão do ponto p
desenhando o resultado em um elemento infinitesimal de volume localizado neste
ponto;
b) a tensão de cisalhamento máxima que ocorre na seção.
Exemplo 03 - As extremidades da viga de madeira devem ser entalhadas como mostra a
figura a seguir. Se a viga tiver que suportar o carregamento mostrado, determine o menor valor
para a profundidade d da viga no entalhe, se a tensão admissível for adm = 3 MPa. A largura da
viga é de 200 mm.
R: d = 62,40 mm
Referências:
HIBBELER, R. C, Resistência dos Materiais, 7ª Edição, Pearson Education, São Paulo,
2010
Marcos Vinício - Apostila de Resistência dos Materiais 2