Campo Magnético gerado por corrente elétrica

Cap014 - Campo magnético gerado por corrente
elétrica
S.J.Troise
14.1
INTRODUÇÃO
Até agora os fenômenos elétricos e magnéticos foram apresentados como fatos
isolados. Veremos a partir de agora que os mesmos fazem parte de uma mesma manifestação
da natureza, ou seja, da carga elétrica apresentada por algumas partículas. Isto nos
permitirá ter uma visão mais ampla do universo físico. Lembremos que corrente elétrica
é carga elétrica em movimento, no caso mais geral os elétrons pois os prótons são
fortemente ligados ao núcleo. Portanto sempre que se tem corrente elétrica, têm-se
carga elétrica em movimento.
14.2
FENÔMENO FUNDAMENTAL: CAMPO MAGNÉTICO GERADO POR CARGA
ELÉTRICA EM MOVIMENTO
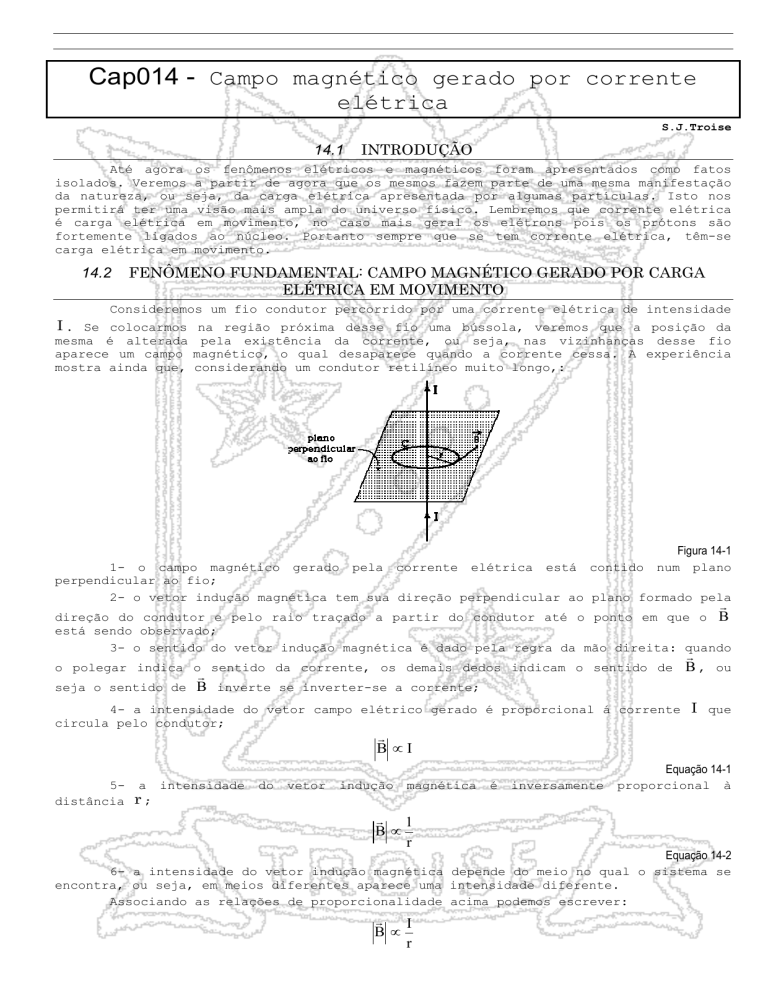
Consideremos um fio condutor percorrido por uma corrente elétrica de intensidade
I . Se colocarmos
mesma é alterada
aparece um campo
mostra ainda que,
na região próxima desse fio uma bússola, veremos que a posição da
pela existência da corrente, ou seja, nas vizinhanças desse fio
magnético, o qual desaparece quando a corrente cessa. A experiência
considerando um condutor retilíneo muito longo,:
Figura 14-1
1- o campo magnético gerado pela corrente elétrica está contido num plano
perpendicular ao fio;
2- o vetor indução magnética tem sua direção perpendicular ao plano formado pela
r
direção do condutor e pelo raio traçado a partir do condutor até o ponto em que o B
está sendo observado;
3- o sentido do vetor indução magnética é dado pela regra da mão direita: quando
r
o polegar indica o sentido da corrente, os demais dedos indicam o sentido de B , ou
r
seja o sentido de B inverte se inverter-se a corrente;
4- a intensidade do vetor campo elétrico gerado é proporcional á corrente I que
circula pelo condutor;
r
B ∝I
5distância
a
r;
intensidade
do
vetor
indução
magnética
r 1
B∝
r
é
inversamente
Equação 14-1
proporcional à
Equação 14-2
6- a intensidade do vetor indução magnética depende do meio no qual o sistema se
encontra, ou seja, em meios diferentes aparece uma intensidade diferente.
Associando as relações de proporcionalidade acima podemos escrever:
r
I
B∝
r
Introdução ã Eletricidade
S.J.Troise
Equação 14-3
Esta nova relação de proporcionalidade pode ser colocada sob a forma de uma
igualdade colocando-se uma constante de proporcionalidade. Trabalhado com unidades do
Sistema Internacional de Unidades, determinou-se que a constante é dada por
µ0
onde
2⋅ π
µ 0 é uma constante denominada permeabilidade magnética do meio e cujo valor para o
vácuo é µ 0 = 4 ⋅ π ⋅ 10 −7 . Assim, podemos escrever:
r
µ ⋅I
B= 0
2⋅π⋅r
Equação 14-4
Que é a expressão que permite calcular a intensidade do vetor indução magnética
gerado por uma corrente num condutor retilíneo longo quando o sistema se encontra num
meio de permeabilidade µ 0 .
Observemos que esta equação pode ser colocada sob a forma
r
B ⋅ 2 ⋅ π ⋅ r = µ0 ⋅ I
Equação 14-5
A qual nos será útil posteriormente.
14.2.1
Exercícios
14.2.1.1 ( ) Um condutor retilíneo muito longo é percorrido por uma corrente de 5 A . Calcule a intensidade do vetor indução
magnética a 10 cm do condutor, supondo que o sistema encontra-se no vácuo.
Resp:
14.2.1.2 ( ) Qual a corrente que deve circular num fio retilíneo muito longo para que a intensidade do vetor indução magnética a 5
cm do mesmo seja 0,5T?
Resp:
14.2.1.3 ( ) Considere dois fios paralelos separados por uma distância de 10 cm, percorridos pela mesma corrente de 0,5 A em
sentidos opostos, no ponto P da figura. . Calcule o vetor indução magnético no ponto P
Resp:
14.2.1.4 ( ) Considere os dois fios da figura acima percorridos pela mesma corrente, porém de mesmo sentido. Calcule o vetor
indução magnético no ponto P.
Resp:
14.2.1.5 ( ) Considere os dois fios da figura abaixo. Calcule o vetor indução magnética por eles gerado quando os fios são
percorridos pela corrente de 3A em duas situações:a) as correntes são de mesmo sentido e b) são de sentidos opostos.
14.3
A LEI CIRCUITAL DE AMPÈRÉ
A Equação 14-5 permite uma generalização muito importante. Para isto definamos o
conceito de circuitação ou circulação do vetor indução magnética.
Consideremos um condutor percorrido por uma corrente I e um caminho qualquer
fechado, que chamaremos de caminho C, que envolva o condutor, conforme a figura ao
lado.
25/5/2005
Teo-14-2005.doc
Página 2 de 6
2
Introdução ã Eletricidade
S.J.Troise
Figura 14-2
Esse caminho fechado é chamado “contorno”
r
ds um deslocamento elementar, isto é, infinitamente pequeno, sobre o
r
caminho C e portanto tangente ao caminho e seja B o vetor indução magnética existente
Seja
na região e gerado pela corrente I .
Por definição chama-se “circulação ou circuitação do vetor indução magnética ao
longo do contorno C”, à integral:
r r
Ci = B ⋅ ds
∫
C
Equação 14-6
Lembremos que essa integral pode ser feita em sentidos opostos sobre o contorno.
Faz-se necessário sempre que se defina o sentido em que a circuitação é calculada,
conforme indicado na figura por uma farpa colocada sobre o contorno.
Figura 14-3
Façamos uma aplicação desta integral calculando a circuitação na situação da
figura acima, na qual se tem um único fio percorrido por uma corrente I e considerando
um contorno circular de raio r . Pode-se observar nessa figura que o deslocamento
r
elementar d s é tangente ao contorno C circular de raio
portanto o produto escalar fica:
r
r e portanto paralelo a B e
r r r r
B ⋅ d s = B ⋅ d s ⋅ cos(0 o )
A Equação 14-6 fica então, lembrando que sobre o circunferência a intensidade do
vetor indução magnética é constante:
∫
∫
C
C
C i = B ⋅ ds = B ⋅ ds
Porém,
∫ ds
é a soma de todos os pedaços infinitamente pequenos existentes sobre
C
a circunferência e portanto é o seu comprimento, ou seja
25/5/2005
Teo-14-2005.doc
Página 3 de 6
2 ⋅ π ⋅ r , Temos portanto que,
3
Introdução ã Eletricidade
S.J.Troise
neste caso, a circuitação se reduz exatamente no primeiro termo da Equação 14-5, ou
seja, podemos escrever:
r r
Ci = B ⋅ ds = µ 0 ⋅ I
∫
C
Equação 14-7
onde I é a corrente que atravessa uma superfície qualquer determinada pelo contorno C.
Pode ocorrer que existam diversas correntes atravessando esta superfície e neste
caso define-se a chamada “corrente concatenada”. Para estabelecer este conceito,
considere a figura abaixo na qual um contorno C tem a superfície por ele determinada
atravessado por diversas correntes em sentidos quaisquer. Todas essas correntes são
chamadas correntes concatenadas pelo contorno. Cada uma dessas correntes será
considerada positiva ou negativa de acordo com a seguinte regra da mão direita: quando
o polegar indicar a direção e o sentido da corrente e os demais dedos indicarem a
sentido de integração a corrente será positiva e negativa caso contrário.
Figura 14-4
Assim, na figura acima, as correntes
I 2 e I 3 são positivas enquanto as correntes
I1 e I 4 são negativas. A medida da correntes concatenada será a soma algébrica dessas
correntes. No caso da figura, ela será:
I CO = −I1 + I 2 + I 3 − I 4
Equação 14-8
A Equação 14-8 deve ser escrita neste caso:
r r
Ci = B ⋅ ds = µ 0 ⋅ I
∫
C
Equação 14-9
Este resultado é chamado Lei Circuital de Ampèré. Sua aplicação só pode ser
feita em situações em que ocorre alta simetria, pois se isto não ocorrer a integração
torna-se extremamente complicada ou até mesmo impraticável.
14.3.1
Exercícios:
14.3.1.1 ( ) Um condutor cilíndrico de raio 4 mm é percorrido por uma corrente de 2 A.. Calcule a intensidade do vetor indução
magnética para pontos internos e externos ao condutor.
Resp:
14.3.1.2 ( ) Um condutor cilíndrico é oco e seus raios interno e externo são respectivamente 0,001 mm e 0,003 mm. Calcule a
intensidade do vetor indução magnética nas três regiões determinadas pelo condutor.
Resp:
14.3.1.3 ( ) Calcule a intensidade do vetor indução magnética no interior de um solenóide de secção retangular cujos raios
interno e externo são respectivamente 0,004 cm e 0,006 cm, supondo que o mesmo é construído em madeira.
14.4
25/5/2005
A LEI DE BIOT-SAVART
Teo-14-2005.doc
Página 4 de 6
4
Introdução ã Eletricidade
S.J.Troise
O vetor indução magnética gerado por um condutor que apresenta uma corrente
elétrica I pode ser calculado por outro processo. Para isto imaginemos um pedaço de
r
r
r
condutor de comprimento ds e seja u o versor de ds no sentido da corrente I que o
r
percorre. Consideremos também um ponto P, a uma distância r de ds onde o vetor indução
r
r
magnética será calculado. Chamemos de r o vetor de posição de P em relação a ds e de
r
u r o seu versor.
Figura 14-5
Sendo o pedaço do condutor infinitamente pequeno, o vetor indução magnética por
ele gerado
magnética
será
também
infinitamente
pequeno.
Chamemos
de
É possível observar-se que o vetor indução magnética
ds apresenta as
r
1- dB
r
2- dB
r
3- dB
r
4- dB
r
dB esse vetor indução
r
dB gerado pelo pedaço
seguintes propriedades:
é proporcional a
ds ;
é proporcional à corrente
I que circula no condutor que contém ds ;
é inversamente proporcional ao quadrado da distância
r;
r
θ é o ângulo entre uv e u r
v r
5- sua direção é perpendicular ao plano que contém u e u r ;
varia proporcionalmente com o sen θ , onde
6- o sentido é dado pela regra da mão direita já apresentada anteriormente.
Podemos colocar as relações de proporcionalidade sob a forma de uma única
relação, escrevendo:
r I ⋅ sen θ ⋅ ds
dB ∝
r2
Esta relação agora pode ser colocada sob a forma de uma igualdade acrescentandose uma constante de proporcionalidade. Trabalhando-se no SI, esta constante assume o
valor
µ0
4⋅π
ou seja, podemos escrever:
r µ I ⋅ sen θ ⋅ ds
dB = 0
4⋅π
r2
r
Por outro lado, sendo dB perpendicular a uv e ur r e sendo seu sentido dado pela
r
regra da mão direita, podemos afirmar que dB esta na direção e sentido do produto
r r
vetorial u ∧ u r que contém a dependência em sen θ e portanto podemos finalmente
escrever:
r µ 0 I ⋅ ur ∧ ur r
dB =
⋅ ds
4⋅π
r2
25/5/2005
Teo-14-2005.doc
Página 5 de 6
Equação 14-10
5
Introdução ã Eletricidade
S.J.Troise
Este resultado é conhecido por Lei de Biot-Savart.
Se considerarmos um condutor muito longo percorrido pela corrente
somar a contribuição de todos os ds que constituem o fio, ou seja:
r
B=
∫
todo
o fio
r
dB =
∫
todo
o fio
I , podemos
r r
µ0 I ⋅ u ∧ u r
⋅ ds
4⋅π
r2
Equação 14-11
14.4.1
Exercícios
14.4.1.1 ( ) Calcule a intensidade do vetor indução magnético produzido por um fio retilíneo, suposto infinito, percorrido por uma
corrente
I , a uma distância r
do mesmo.
Resp.:
14.4.1.2 ( ) Se a corrente que circula no fio do exercício anterior é de 2 A, calcule a intensidade do vetor indução magnética a
uma distância de 0,5m
Resp.:
14.4.1.3 ( ) Considere uma espira circular de raio R . , isto é, um fio de forma circular, percorrido por uma corrente I . Calcule a
intensidade do vetor indução magnética gerado num ponto P sobre o eixo de simetria da espira, e a uma distância r do plano da
mesma.
Resp.:
14.4.1.4 ( ) Considerando a resposta do item anterior, calcule a intensidade do vetor indução magnética no centro da espira.
Resp.:
R . sobre o qual se enrola espiras de fio condutor, que
contém N espiras por unidade de comprimento, percorridas por uma corrente I . Calcule a intensidade do vetor indução magnética
14.4.1.5 ( ) Considere um solenóide, isto é, um tubo cilíndrico de raio
num ponto qualquer no interior do solenóide e sobre o eixo deste.
Resp.:
25/5/2005
Teo-14-2005.doc
Página 6 de 6
6