Document

Dispositivos Eletrônicos
Aula 10: Princípio de funcionamento
de transistores bipolares (2/2)
1
Plano da Aula
• Regime ativo reverso (para poder entender a
saturação)
• Regime de saturação (direta)
• Limitações/efeitos parasitas:
– Efeito Early
– Ruptura
– Variações com a temperatura
– Limitação na potência dissipada
2
Relembrando…
VCE=VBE+VCB
• podemos ter 4 possibilidades para as 2 junções:
• B-E diretamente, B-C inversamente : Região ativa direta
• B-E diretamente, B-C diretamente
: Região de saturação
• B-E inversamente, B-C inversamente: Região de corte
• B-E inversamente, B-C diretamente : Região ativa inversa
3
Regime Ativo Direto
Até agora vimos o regime ativo direto (Forward):
Diretamente
polarizada
Reversamente
polarizada
Consideraremos as
seguintes relações de
dopagem(não universais):
N D − E > N A− B > N D −C
=>Emissor mais dopado do
que a base, que é mais
dopada do que o coletor.
4
Regime Ativo Inverso
Se invertermos as polarizações, operaremos o transistor no
regime ativo inverso (Reverse):
Diretamente
Reversamente
polarizada
polarizada
Regime ativo inverso:
junção B-E: reversamente
junção B-C: diretamente
N D − E > N A− B > N D −C
Por conta da dissimetria da estrutura,
5
BR<<BF (por vezes menor que 1!)
Regime de Saturação
Mas e se polarizarmos diretamente as
junções B-E e B-C?⇒ Regime de Saturação!!
Em termos de densidade de
portadores,
há
uma
“superposição” de curvas
na base.
Observe que o gradiente
na Base diminuiu: para IE
fixo, IC diminui!!
6
Regime de Saturação
Regime de saturação:
Observe a configuração!
7
O modelo Ebers-Moll
Como um modelo equivalente “completo” deve ser fiel à realidade,
deve prever o comportamento tensão-corrente sob qualquer modo
Modelo Ebers-Moll
de operação:
VBE < 0, VBC > 0
VBE > 0, VBC < 0
αF =
βF
βF +1
αR =
βR
βR +1
3 parâmetros: IS, αF e αR!
8
Ebers-Moll: exemplo
Tentemos simular as correntes na condição
abaixo (saturação), usando o modelo Ebers-Moll:
VBE = VBC = 0,7V
αF =
αR =
Apenas
3 parâmetros:
IS, βF e βR
ou:
IS,αF e αR
I DE ≈
I DC ≈
βF
βF +1
βR +1
IS
⋅ exp(
VBE
)
VT
IS
⋅ exp(
VBC
)
VT
αF
αR
βR
9
Ebers-Moll: exemplo
Vamos às “continhas” :
βF
100
= 0,990099
β F + 1 101
βR
6
αR =
= = 0,8571429
βR +1 7
VBE = VBC = 0,7V
αF =
=
I DE
10 −14
0,7
=
⋅ exp(
) = 5,7272 mA
0,990099
0,0258649
I DC
10 −14
0,7
=
⋅ exp(
) = 6,6155 mA
0,8571429
0,0258649
I C = α F ⋅ I DE − I DC = 0,990099 ⋅ 5,7272 ⋅10 −3 − 6,6155 ⋅10 −3 = −945 µA
I E = I DE − α R ⋅ I DC = 5,7272 ⋅10 −3 − 0,8571249 ⋅ 6,6155 ⋅10 −3 = 56,89 µA
I B = I E − I C = 56,89 µA + 945 µA = 1,002 mA
10
Ebers-Moll: exemplo
Comparando com os valores calculados:
I C = −945 µA
I E = 56,89 µA
No PSPICE, a referência
da corrente é “entrar no
dispositivo”
I B = 1,002 mA
E com uma ajudinha de software numérico
(tal como o Scilab), o que dá pra fazer?
11
Ebers-Moll: exemplo
// Função para calcular correntes com base no modelo Ebers-Moll
// (3 parâmetros apenas) e as condições de contorno VBE e VCE (VBC=VCE-VBE)
function [ic,ie,ib]=ebersmoll(is,betaf,betar,vbe,vce);
alfaf=betaf/(betaf+1);
// defina alfaf em função de betaf
alfar=betar/(betar+1);
// defina alfar em função de betar
ide=is/alfaf*exp(vbe/0.0258649);
//cacule IDE
idc=is/alfar*exp((vbe-vce)/0.0258649); // cacule IDC
ie=ide-alfar*idc;
// calcule IE
ic=(alfaf*ide-idc);
// calcule IC
ib=ie-ic;
// calcule IB=IE-IC
endfunction
vce=[0:0.01:0.7];
//vetor de pontos de VCE: 0 a 0.7 V, passo de 10 mV
for i=1:length(vce),
// para cada valor do vetor de pontos, faça:
[ic,ie,ib]=ebersmoll(1e-14,100,6,0.7,vce(i));
//calcule as correntes
meuic(i)=ic;
// aproveite apenas IC, num vetor
end
plot2d(vce,meuic);
// plote o vetor de IC em função de VCE
12
Ebers-Moll: exemplo
Veja o resultado do Scilab:
13
Ebers-Moll: exemplo
Veja o resultado do PSPICE:
Compare com o Scilab!!!
14
Regiões
Saturação profunda (VCB ≤ -0,5 V)
Saturação (VCB ≤ 0V)
: diminuição de IC apreciável!!
Região ativa (VCE≥VBE→ VCB ≥ 0)
VBE=0.750V
IC
VBE=0.725V
{
VBE=0.700V
Saturação leve (efeitos em IC ainda imperceptíveis)
VCE
VBE=0V
Corte:
VBE ≤ 0,4 V
→ IC≈0
15
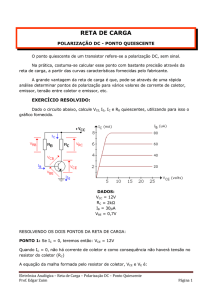
Limitações
Será que é uma fonte de
corrente ideal (resistência
paralela infinita)? Será que o
IDEAL existe de verdade????
Será que posso aumentar VCE
tanto quanto “Siqueira”? Posso
colocar 1 MILHÃO DE volts???
16
Limitações
Efeito Early: modulação da largura efetiva da base
Impacto no gradiente de minoritários na Base (elétrons em um NPN, lacunas
em um PNP)
J. Early, “Effects of space-charge layer widening in junction transistors,”
Proceedings of the IRE, vol. 40, no. 11, pp. 1401–1406, Nov. 1952.
17
Limitações
Com o aumento de VCB (VCE), o
gradiente de minoritários na Base
aumenta: a corrente de coletor
aumenta!! Efeito “quasi-linear”
Se o
gradiente
aumenta, IC
aumenta
VA é a tensão de Early (ai ai ai, mais
um parâmetro do modelo...)
18
Limitações
Modelando o efeito Early:
IC
Regra de triângulos, pra você
matar a saudade do 2º Grau!!!!
-VA
I C (VCE = V A ) = 2 ⋅ I C ("VCE = 0" )
IC2
IC1
VCE1
V CE
VBEBE
I S ⋅ exp(
) ⋅ (1 +
)
VT
VA
VCE2
VCE
OBS: diferentemente
dos livros, no PSPICE
o termo corretivo é
(1+VCB/VA)!
Ao considerar o efeito Early, é preciso conhecer os
parâmetros IS e VA do transistor para determinarmos IC.
Em geral, o impacto em IB pode ser desprezado.
19
Limitações
Uma continha não faz mal a ninguém...
IC (mA)
V BE = 0 , 7V
8
5
∆I=3 mA
∆I=5 mA
-VA
1
∆V=VA+1 V
I S ⋅ exp(
V BE
V
) ⋅ (1 + CE )
VT
VA
5 mA = I S ⋅ exp(
11
VCE (V)
∆V=10 V
Usando a expressão dos livros (ao lado),
determine IS e VA, com base nos dados
experimentais acima.
V A + 1V → 5 mA
5 mA ⋅ 10 V
VA =
− 1V = 15 , 667 V
10 V → 3 mA
3 mA
0 ,7
1
) ⋅ (1 +
) ⇒ I S = 8 , 289 ⋅ 10 −15 A
0 , 0258649
15 , 667
20
Limitações
E seu eu quiser comparar com o PSPICE???
IC (mA)
V BE = 0 , 7V
8
5
∆I=3 mA
VBE=0,7 V⇒
VCB=VCE-0,7 V
-VA
0,3
V BE
V
) ⋅ (1 + CB )
VT
VA
VCB (V)
∆V=10 V
∆V=VA+0,3 V
I S ⋅ exp(
10,3
∆I=5 mA
Usando a expressão DO PSPICE (ao lado),
determine IS e VA, com base nos dados
experimentais acima.
V A + 0 ,3V → 5 mA
5 mA ⋅ 10 V
VA =
− 0 ,3V = 16 ,367 V
10 V → 3 mA
3 mA
5 mA = I S ⋅ exp(
0 ,7
0 ,3
) ⋅ (1 +
) ⇒ I S = 8 , 659 ⋅ 10 −15 A
0 , 0258649
16 ,367
Vamos Simular?
21
Limitações
Implementando o modelo no PSPICE:
22
Limitações
E aí, bateu??
Não se preocupe, você não vai ter que “decorar” 2 expressões. Use a
dos livros. Em casos específicos para comparação com o PSPICE,
eventualmente usaremos a outra. Em todo caso, as diferenças são, em
23
geral, muito pequenas.
Limitações
Existe um limite de VCB, acima do qual a junção B-C “rompe”. Em geral, deseja-se que
este limite seja o maior possível, portanto em geral o processo de ruptura é por
24
avalanche (coletor pouco dopado)
Limitações
Em geral, IC>>IB e VCE>VBE. A potência dissipada no
dispositivo é praticamente o produto IC⋅VCE
+
RTH
Potência
dissipada
Temperatura da
junção
ambiente
A conversão de potência em
temperatura é numericamente
calculada através da resistência
térmica do componente:
RTH
∆T
K
ºC
Unidade = ou
=
W
W
∆P
TJunção = T0 + RTH ⋅ P
Em Si (silício), a temperatura
máxima é da ordem de 150 a 200ºC
Exemplo: se RTH=100K/W, e T ambiente é de 25ºC, a máxima potência 25
dissipada é de 1.75W, para uma temperatura de junção máxima de 200ºC!
Limitações
Com o aumento de temperatura, um menor VBE é
necessário para manter uma mesma corrente de
coletor:
Se fixarmos VBE e VCE com o
transistor em um alto nível
de potência, o aquecimento
leva a um aumento de IC (já
que VBE é fixo) que aumenta
a potência (já que VCE é fixo),
que aumenta a temperatura,
que aumenta IC, que aumenta
a potência... e kabum!!!
Observe o mecanismo de
realimentação positiva.
Tal como no caso do diodo de silício, considere uma variação
de -2mV/°C a corrente de coletor constante.
26
Limitações
Efeito da temperatura e do nível de corrente no ganho
de corrente de um transistor bipolar Si:
Se fixarmos IB e VCE com o
transistor em um alto nível
de potência, o aquecimento
leva a um aumento de IC
(pois β aumenta) que
aumenta a potência (já que
VCE é fixo), que aumenta a
temperatura, que aumenta
IC, que aumenta a potência...
e kabum!!! Observe o
mecanismo de realimentação
positiva.
β varia com a corrente e com a temperatura!!!
27
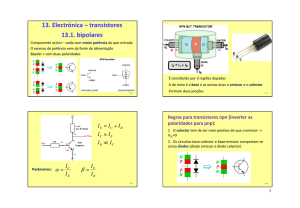
Limitações
Além disso, resistências de acesso e capacitâncias de
difusão/junção. (e eu que pensei que era fácil...)
28
Modelo PSPICE
Em um modelo SPICE, encontramos os seguintes
parâmetros:
BF
: Ganho de corrente em modo ativo direto
BR
: Ganho de corrente em modo ativo reverso
IS
: Corrente de saturação
VAF
: Tensão Early em modo direto
VAR
: Tensão Early em modo reverso
NF
: Fator de idealidade em modo direto (η)
NR
: Fator de idealidade em modo reverso
Rb
: Resistência de acesso da Base
... E mais um monte de parâmetros para modelagem das
variações com o nível de corrente, temperatura, ...
29
Exemplo de
especificações
30
Resumo dos pontos
importantes
• Transistor bipolar: dispositivo em estado
sólido que pode dar ganho de potência (ativo)
• O efeito transistor é o controle da corrente de
coletor através da tensão de controle aplicada
na junção base-emissor
• O dispositivo, como qualquer outro, apresenta
limitações ligadas à sua construção física
• As aplicações são inúmeras (veremos a seguir)
31
Cronograma de
atividades
• Não pense que você vai aprender revisando os slides:
LEIA O LIVRO! Sugere-se o seguinte cronograma:
Atividade
Duração
Razavi: Seções 4.4.5,4.5, 4.6 até 4.6.2 (incluso)
60 minutos
Revisão dos slides
45 minutos
Resolução analítica das questões
(10 minutos/questão)
30 minutos
Simulação das questões (6 minutos/questão)
30 minutos
Total: 2h45min de atividades. Se você levar muito mais
tempo do que esta previsão, converse com o professor.
32
Exercícios: trazer antes
da próxima aula
As questões são individuais, use a
tabela de valores!
33
Exercícios pra trazer na
próxima aula
Esta questão não requer resposta analítica, apenas simulação. Considerando o modelo
ORIGINAL PSPICE do transistor 2N2222, aplique o valor de corrente de base indicado (IBX)
e determine, para este transistor e valor de corrente de base, o valor do ganho de
corrente direto (βF=IX/IBX) e reverso (βR=IY/IBX). Observe atentamente as disposições do
transistor: provavelmente você fará uso de rotação (CTRL+R) e espelhamento (CTRL+F).
34
Exercícios pra trazer na
próxima aula
Observe que nos circuitos abaixo, as 2 junções (B-E e B-C) estão polarizadas diretamente.
Utilize um transistor para o qual IS=10-14 A, BF=100 e BR=BREV. Com a ajuda do modelo
Ebers-Moll, calcule as correntes de base, coletor e emissor (utilize VT=0,0258649 V) em
cada caso. Implemente o modelo no PSPICE, simule e compare resultados (erro esperado
menor que 2%). Depois comente: com uma tensão direta de 0,5 V na junção B-C (circuito
à direita), já se observa um “grande impacto” nas correntes de base e coletor, se
comparadas ao regime ativo?
35
Exercícios pra trazer na
próxima aula
Considere um transistor para o qual IS=10-14 A, BF=100 e VA=VEARLY. Com a ajuda do
modelo na página 19 (expressão dos livros), calcule IC nos seguintes casos:
(a) VCE=1 V
(b) VCE=5 V
(c) VCE=20 V
Implemente o modelo no PSPICE, simule e compare resultados (erro esperado <5%).
36
Exercícios pra trazer na
próxima aula
Considere um transistor para o qual IS=10-14 A, BF=100.
Determine a tensão no emissor (em relação ao terra) quando
uma corrente IE0 é forçada no emissor. Compare seu valor
com uma simulação em 27 °C. Agora considerando uma
variação fictícia de -2mV/°C (chamaremos de φ) em VBE a IC
(≈IE) constante, calcule o novo valor de VBE em: (a) T=-25 °C,
(b) T=50 °C, (c) T=75 °C.
Simule o circuito nestas temperaturas, e com base em seus
resultados DE SIMULAÇÃO, implemente uma função da forma
VBE(T)=K1-K2·(T - 27 °C). Nesta sua função, o valor de φ estará
naturalmente explícito. Qual a diferença percentual em
relação ao valor -2mV/°C? (diferença esperada < 25%). Agora
inverta a função, para que, dado VBE, você encontre T (ou seja
T=f(VBE)) para a faixa de temperatura considerada (-25 a 75
°C). Você pode fazer um sensor de temperatura com o
circuito!
37
Exercícios pra trazer na
próxima aula
Preste bastante atenção nesta questão, ela é interessante pra você botar os neurônios
pra pensar. A questão não requer resposta analítica, apenas simulação. Você irá comparar
o impacto na corrente de coletor de dois efeitos distintos: o Efeito Early (com
temperatura fixa), e o aumento do β em função da temperatura (com VCE fixo).
Considerando o modelo ORIGINAL PSPICE do transistor 2N2222, e uma temperatura
default de 27 °C, simule o circuito mostrado inicialmente com VCE=1 V. Anote o valor da
corrente de coletor (este valor será nomeado IC1).
Em seguida, e na mesma temperatura, faça VCE=5
V. Anote o valor da corrente de coletor (IC2). Com
base neste novo valor e na diferença de 4 V em
VCE, determine a tensão de Early do transistor
(ver slide 21). Abra o modelo, e compare com o
valor de VAF. Em seguida, coloque a temperatura
em 37 °C (apenas 10 °C a mais) e VCE=1 V. Anote o
valor da corrente de coletor (IC3). Compare IC3 e IC2.
Finalmente, faça VCE=5 V (com 37 °C), e anote o valor da corrente de coletor (IC4).
Agora olhe o próximo slide...
38
Exercícios pra trazer na
próxima aula
Se você medisse o transistor com VCE em 1V, e a pequena potência dissipada (já que VCE é
pequeno) fosse tal que a temperatura do transitor se elevaria apenas de 2,5 °C em
relação a uma sala em 24,5 °C, você iria medir o valor IC1. Ao mudar VCE para 5V
(portanto multiplicando a potência dissipada por 5 vezes, se desprezarmos a variação em
IC), a temperatura do transitor se elevaria de 5·2,5 °C=12,5 °C em relação à sala em 24,5
°C, e você mediria IC4. Se no momento do experimento você usasse a regra de triângulos
(pag. 13) para determinar VAF a partir de IC1 e IC4, que valor acharia? Este valor
corresponde ao valor no modelo? Qual o erro?
Veja que o problema acima é que você não levou em conta o impacto da variação do β
com a temperatura. Agora bote todos os seus neurônios para, juntos, responderem à
questão:
Se, para ganhar o emprego na empresa dos seus
sonhos, você tivesse que modelar corretamente a
tensão de Early do transistor, em que níveis de
potência/IC/VCE você faria o experimento?
39