SUB-PROJETO DE PESQUISA: IMAGEM MATEMÁTICA

PROJETO DE PESQUISA: IMAGEM MATEMÁTICA
Esequiel R. Oliveira UERJ (Coord. da Pesqisa: Imagem Matemática)
Maria Ignez Rocha David (Pesquisadora – Professora do Instituto de Aplicação da UERJ)
RESUMO
Esta comunicação pretende apresentar a pesquisa – em andamento – que investiga a aplicação
de aspectos da teoria lingüística à leitura/produção do texto visual, de modo a qualificar a sua
contribuição na produção do conhecimento escolar. Propõe uma reflexão sobre a associação do instituto
do Signo Lingüístico (Schaff, 1968; Peirce, 2000) à Teoria Gerativa (Chomsky, 1986), com vistas ao
aproveitamento da competência lingüística do aluno expressa na leitura de imagem: desde signos visuais
mínimos até estruturas significativas complexas. Considerando que no sentido amplo qualquer produção
humana dotada de sentido é um signo, a pesquisa pretende estabelecer – sem prejuízo da marca
polissêmica da imagem – bases para subsidiar a produção de seqüências didáticas onde o uso da
imagem na prática pedagógica cotidiana se sustente cientificamente. No que diz respeito à sua
adequação e potencialidade em determinado contexto. A pesquisa prevê três etapas: (i) a
fundamentação teórico-conceitual, (ii) a análise de diferentes propostas de utilização da imagem no livro
didático de matemática e (iii) a criação e testagem de seqüências didáticas onde o uso da imagem
apresente eficácia comprovada na produção do conceito matemático.
INTRODUÇÃO
A linguagem é uma forma de organizar o mundo e de compreendê-lo; é uma ferramenta de
comunicação entre indivíduos e de distinção entre culturas; é um meio identificar as coisas do mundo
físico e de distinguir duas idéias de modo claro e constante 1. Muitas são as definições possíveis para
linguagem, no entanto todas, possivelmente convergem para um ponto comum ao universo aqui tratado,
o conhecimento – no Ensino Básico. Qualquer que seja a abordagem (específica ou geral) o
conhecimento é a substância da experiência escolar. É comum dizer-se que a produção escolar
imprescinde do conhecimento de mundo do aluno. Desse modo a linguagem que é responsável pela
inserção da criança no mundo cultural e social, antes mesmo da sua chegada à escola, recebe desta um
tratamento especial, investigativo e normativo. Visando não apenas a comunicação e a compreensão do
que é visível – uso predominante da linguagem na infância – mas também da dimensão abstrata do
conhecimento. Quando a linguagem torna-se objeto de conhecimento em si.
Esse novo universo desvenda, para a criança, o mistério de como se produz o registro de uma
história, já que a criação é fácil para ela. E, embora ela saiba que os livros registram (contam) histórias e
que a escola é o lugar onde se aprende os segredos da escrita, possivelmente a atitude de surpresa
diante da amplitude da ciência lingüística – ainda que tratada em seu nível – seja um fato que se repete
durante toda experiência escolar. Inclusive pelo fato de ser a linguagem matéria de estudo obrigatório
durante toda formação básica. Até aqui há uma simplificação de conceito, uma vez que o uso do termo
linguagem está associado à palavra falada ou escrita. Ocorre, porém, que a linguagem verbal não é a
única existente2, há diversos sistemas lingüísticos. Entretanto, para ser fiel à definição apresentada no
início deste texto, todos estão relacionados à compreensão do mundo, à categorização das coisas e das
ações humanas, estabelecendo diferenças e significados que variam de acordo com os grupos sociais,
sejam elas pequenos ou grandes. Ao ouvirmos tal grito agimos de forma particular numa atitude que
reúne cautela, curiosidade, solidariedade. A correspondência entre a idéia (significado) e o som
(significante) constitui a estrutura da linguagem, o signo (Saussure, 1969) 3.
1
Saussure (1969)
Fiorin (2002) p. 58
3 Saussurre (1969)
2
Embora a definição de signo proposta por Saussurre esclareça a importância da linguagem na
produção de sentido, ela restringe o conceito à linguagem verbal quando afirma ser aquele a união de um
significado a uma imagem sonora. Todavia é possível ampliar a noção de significante sem prejuízo da
relação significante/significado, conforme propõem Barthes (1990) e Fiorin (2002) 4. E é sobre essa
proposta que se fundamenta essa argumentação. Que tem por objetivo promover uma reflexão sobre a
relação entre alguns aspectos da teoria lingüística (verbal) e a leitura /produção do texto (mensagem)
visual, de modo a qualificar a contribuição deste na produção do conhecimento escolar em geral e na
aprendizagem matemática em particular.
JUSTIFICATIVA
Sendo a linguagem visual um sistema de signo que precede a fala e a escrita mas que
permanece presente nas produções humanas nas mais variadas formas, desde as artísticas até os sinais
de comunicação, há que se supor que a sua estrutura seja objeto durante a formação escolar. Mas, se de
um lado isto já ocorre nas aulas de artes de outro este exercício freqüentemente se restringe a estes
espaços.
Tal fato não se verifica no uso da linguagem verbal. O uso de formas descritivas: relatórios,
descrições e histórias são comuns em todos momentos da atividade escolar, tanto fornecidas pelo
professor quanto solicitadas ao aluno. Mesmo que se diga que os desenhos dos alunos são comuns nas
aulas, que os mapas, as ilustrações dos livros, os cartazes e os vídeos são exemplos da presença da
imagem no âmbito escolar, ainda assim não se poderia creditar a tal presença um exercício lingüísticovisual consciente. Pelo simples fato de que a formação do educador não inclui um exercício de
competência nessa linguagem5. Isto é, não há clareza sobre um conhecimento do signo visual que
possibilite a produção de significados em diversas áreas de conhecimento.
Ao contrário, é comum dizer-se que tal competência é um talento concedido a poucos. O que
permite presumir a aplicação do conceito de leitura e expressão imagética com vistas a produção de
novos signos estão restritos a setores particulares como o da criação artística ou da habilidade para
reprodução de imagens. Desprezando-se, dessa forma, a hipótese de que a linguagem no sentido amplo
não se restringe a essas finalidades específicas. Pois se assim fosse somente estenógrafos, poetas,
cronistas e romancistas produziriam conhecimento através da linguagem verbal. A competência
lingüístico-visual é inerente aos humanos habilitados ao sentido da visão. Mesmo admitindo eventual
polêmica à essa afirmativa no que concerne, por exemplo, à percepção espacial proporcionada pelo tato,
ela está aqui posta com a finalidade de delimitar o espaço da reflexão, uma vez que trataremos de
Signos Visuais. Termo que doravante será utilizado especificamente para a linguagem visual. Enquanto
que em referência a abordagem verbal (ou mesmo geral) do conceito será usado apenas a expressão
signo.
METODOLOGIA
A fim de subsidiar esta reflexão, serão apresentadas analogias entre alguns aspectos da teoria
geral dos signos, relevantes ao signo visual, que potencialize o aproveitamento da idéia da competência
lingüístico-visual no desenvolvimento da habilidade de leitura de imagem e seu aproveitamento na prática
cotidiana da construção do conhecimento escolar. Tais analogias serão fundamentadas em três
abordagens do tema: (i) a composição do signo, (ii) o estudo de suas características e (iii) a classificação
dos signos. Cada abordagem será composta de uma base teórico-conceitual que sustente a proposição
Barthes (1990) p.43: “Hoje é necessário ampliar a noção totalizante de liíngua, sobretudo do ponto de vista
semântico: a liígua é a abstração totalizante das mensagens emitidas erecebidas”. Fiorin (2002) p.58: “Não se pode
falar em imagens acústicasquando se trabalha com outros sistemas de signos. Por isso é necessário ampliar a noção
de significante para que ela possa ser usada em todas as linguagens”.
5 Chomsky (1986) Descreve a gramática universal: a capacidade linguística humana, determinada geneticamente. O
que pressupõe um conhecimento lingüístico comum a todos os falantes em qualquer língua, independente de um
processo de escolarização.
4
de atividades cuja testagem indicará caminhos para análise, seleção e adequação de imagens na
elaboração de seqüências didáticas no ensino de matemática.
RELATO DE EXPERIÊNCIA
Como forma de exemplificar a pesquisa apresenta-se seguir o relato de uma experiência que
aborda o uso de imagens homotéticas como ferramenta na compreensão das operações com números
racionais. Onde a discussão se dá em torno de proposições de alteração das dimensões de figuras
semelhantes (através de transformações no plano) e da coerência destas com as suas traduções
aritméticas (ou vice-versa). Nesse caso, todo conceito se constrói com a intermediação da imagem 6.
Todavia, apesar de bem sucedida a experiência, em alguns momentos do processo verificou-se
fatos relativos à compreensão – à composição do signo – das figuras utilizadas, o que motivou a
substituição de algumas. A avaliação desses fatos levou a conclusão de que a imagem pode contribuir
ou comprometer a aprendizagem escolar, por isso exige seleção cuidadosa e consciente.
Uma rápida reflexão sobre esta conclusão associada a avaliação preliminar de alguns livros
didáticos permite caracterizar o uso da imagem na sala de aula da seguinte forma:
(a)
pode intermediar a construção do conceito viabilizando a produção (formalização) do
texto matemático;
(b)
pode ilustrar demonstrações desenvolvidas em linguagem matemática, com vistas a
identificar aplicações de determinados conceitos;
(c)
pode ser irrelevante para o processo de aprendizagem ou até comprometê-lo.
CONCLUSÃO
A pesquisa pretende, portanto, numa de suas etapas investigar o tema nestes domínios.
Identificar situações (na pesquisa em material didático e na realização de experiências pedagógicas) que
exemplifiquem os três casos e determinar suas causas à luz da semiologia da imagem. E desse modo
contribuir para a escolha de imagens, consciente e cientificamente sustentável, na produção de material
didático.
BIBLIOGRAFIA:
BARTHES, R. O Óbvio e o Obtuso: ensaios críticos III. Tradução Lea Novaes. Rio de Janeiro:
Nova Fronteira, 1990.
CHOMSKY, N. O Conhecimento da língua: sua natureza, origem e uso. Tradução Anabela
Gonçalves e Ana Teresa Alves. Lisboa: Editorial Caminho, 1986.
FIORIN, José luiz. Introdução à lingüística I. Objetos teóricos. São Paulo: Contexto: 2002.
LURIA, A. R. Pensamento e Linguagem. Últimas conferências de Luria.Porto Alegre: Artes
Médicas, 1987.
PEIRCE, C. S. Semiótica. Tradução J. Teixeira Neto. São Paulo: Editora Perspectiva, 2000.
SAUSSURE, Ferdinand. Curso de Lingüística Geral. São Paulo: Cultrix/Edusp, 1969.
6
Ver relatório da experiência em anexo.
ANEXO
MULTIPLICAÇÃO DE NÚMEROS RELATIVOS ATRAVÉS DE HOMOTETIAS
Maria Ignez Rocha David
Objetivo: conceituar produto de números relativos através da composição de homotetias. As
demonstrações ou mesmo outros argumentos que justificam as regras de sinais para o produto de
números relativos, para a maioria dos alunos de 6ª série, são muito abstratos, sem significado.
Trabalhando com a composição de homotetias, os alunos estabelecem tais regras de forma conclusiva,
observando as figuras construídas. Em futuras discussões, o professor rapidamente retoma as regras
concluídas, pois as imagens são facilmente resgatadas da memória dos alunos.
I) HOMOTETIAS
A transformação denominada homotetia possui um ponto fixo, que também se chama centro da
homotetia, e um número pelo qual se multiplica a distância de cada ponto a esse centro. Esse número é
dito razão da homotetia.
Para encontrar a figura transformada, liga-se cada ponto da figura dada ao ponto fixo e marcase, a partir desse centro, a nova distância, resultado da multiplicação da distância inicial pela razão.
OBS: O centro, cada ponto inicial e seu transformado encontram-se sobre uma mesma reta.
ATIVIDADES
1) a) Desenhe uma bandeirinha e escolha fora dela um ponto que será o centro da homotetia.
b) Encontre a nova localização dos vértices, multiplicando por 2 as distâncias.
c) Desenhe a nova figura.
OBS: chame de A, B, C, ... os pontos da figura inicial e de A’, B’, C’, ... os novos pontos.
2) Faça para a figura abaixo a homotetia pedida:
O  Ponto fixo
/
razão: 3/5
II) COMPOSIÇÃO DE HOMOTETIAS DE MESMO CENTRO ( 1ª Parte )
A cada figura aplique a composição de homotetias proposta pelo esquema e encontre a razão da
homotetia que leva diretamente a primeira figura à última. Você deve colorir cada figura encontrada de
uma cor diferente.
2) FIG ABCDE
x2

FIG A’B’C’D’E’
R = 4/3

x 2/3
FIG A”B”C”D”E”
III) HOMOTETIA DE RAZÃO NEGATIVA
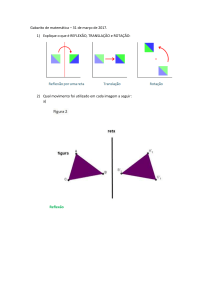
1) Desenhe um triângulo qualquer no centro desta folha, com base paralela ao seu rodapé e um
ponto P no prolongamento desta base, situado a 2 cm do vértice direito do triângulo. Este ponto
será o centro das homotetias. Chame o triângulo de figura 1.
a) Efetue uma homotetia de razão 2 sobre a figura 1, encontrando a figura 2.
b) Efetue uma homotetia de razão – 2 sobre a figura 1, encontrando a figura 3.
IV) COMPOSIÇÃO DE HOMOTETIAS DE MESMO CENTRO ( 2ª Parte)
1) Efetue as composições de homotetias de acordo com os esquemas dados. Determine também a
razão da homotetia que leva diretamente a primeira figura à última.
a) Fig ABC
--- x 2  Fig A”B”C” --- x(-3) 
--
Fig A”B”C”
x(-6) 
C’
b) Fig ABCDE -- x (-1)  Fig A’B’C’D’E’ -- x (-1/2)  Fig A”B”C”D”E”
-- x ( 1/2 ) 
B’