Resoluções das atividades

FÍSICA 2
Resoluções das atividades
Aula 13
Eletrodinâmica III – Resistores
Série
30 Ω
10 Ω
Atividades para sala
12 V
30 Ω
20 Ω
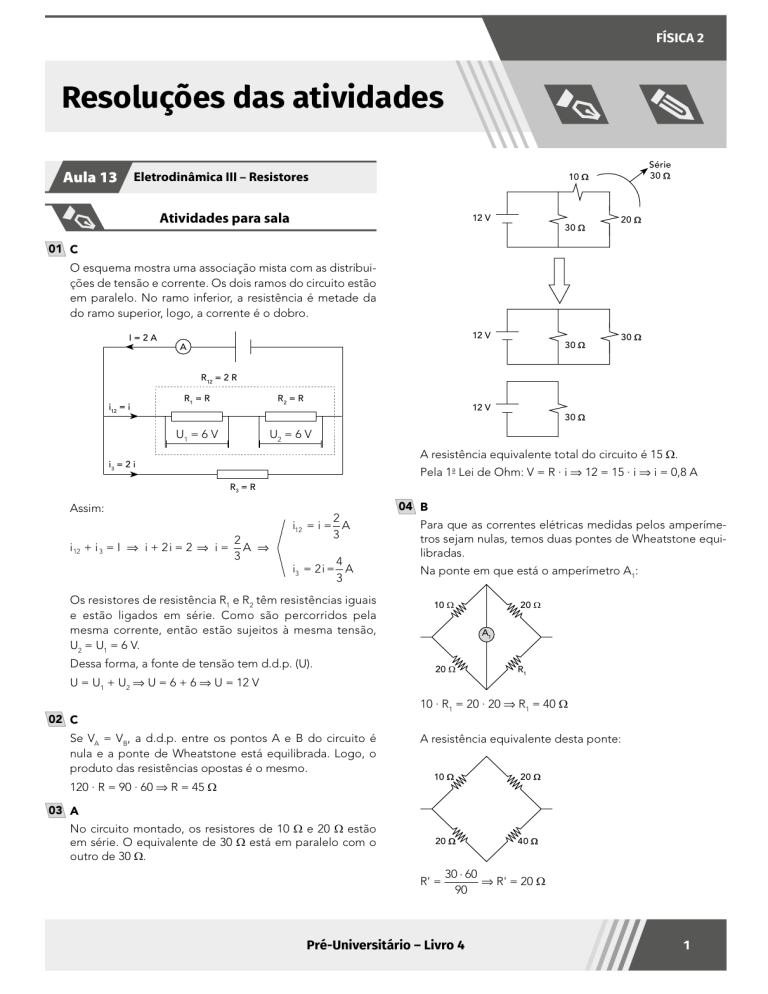
01 C
O esquema mostra uma associação mista com as distribuições de tensão e corrente. Os dois ramos do circuito estão
em paralelo. No ramo inferior, a resistência é metade da
do ramo superior, logo, a corrente é o dobro.
I=2A
12 V
30 Ω
A
30 Ω
R12 = 2 R
i12 = i
R1 = R
R2 = R
U1 = 6 V
U2 = 6 V
12 V
i3 = 2 i
A resistência equivalente total do circuito é 15 Ω.
Pela 1a Lei de Ohm: V = R · i ⇒ 12 = 15 · i ⇒ i = 0,8 A
R3 = R
Assim:
2
i12 + i 3 = I ⇒ i + 2i = 2 ⇒ i = A ⇒
3
04 B
2
i12 = i = A
3
4
i3 = 2i = A
3
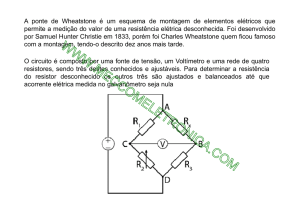
Para que as correntes elétricas medidas pelos amperímetros sejam nulas, temos duas pontes de Wheatstone equilibradas.
Na ponte em que está o amperímetro A1:
Os resistores de resistência R1 e R2 têm resistências iguais
e estão ligados em série. Como são percorridos pela
mesma corrente, então estão sujeitos à mesma tensão,
U2 = U1 = 6 V.
Dessa forma, a fonte de tensão tem d.d.p. (U).
U = U1 + U2 ⇒ U = 6 + 6 ⇒ U = 12 V
10 Ω
20 Ω
A1
20 Ω
R1
10 · R1 = 20 · 20 ⇒ R1 = 40 Ω
A resistência equivalente desta ponte:
02 C
Se VA = VB, a d.d.p. entre os pontos A e B do circuito é
nula e a ponte de Wheatstone está equilibrada. Logo, o
produto das resistências opostas é o mesmo.
120 · R = 90 · 60 ⇒ R = 45 Ω
03 A
30 Ω
10 Ω
20 Ω
20 Ω
40 Ω
No circuito montado, os resistores de 10 Ω e 20 Ω estão
em série. O equivalente de 30 Ω está em paralelo com o
outro de 30 Ω.
R' =
30 ⋅ 60
⇒ R' = 20 Ω
90
Pré-Universitário – Livro 4
1
FÍSICA 2
Para a ponte na qual está o amperímetro A2 ficar equilibrada, o produto das resistências opostas é o mesmo.
20 Ω
03 D
Com a chave K aberta, o circuito equivalente é o seguinte:
60 Ω
R
A2
30 Ω
R
R
⇒i =
i A
R2
ε
3R
ε
Com K fechada, o circuito equivalente passa a ser o
seguinte:
20 · R2 = 60 · 30 ⇒ R2 = 90 Ω
Atividades propostas
3R
01 A
3R ⋅ 2R
5R
6R
5
2R
Como a ponte de Wheatstone está equilibrada, a resistência ligada entre os pontos B e D não funciona.
i' A
⇒
i' A
⇒ i' =
2R
ε
ε
A
B
Portanto:
5ε
i' 6R 5
=
= ⇒ i' = 2, 5i
ε
2
i
3R
2R
Re =
2R
⇒ Re = R
2
04 C
02 B
Como as três lâmpadas são idênticas, todas têm a mesma
resistência.
127 V

R
Corrente total:
Corrente no amperímetro (i2):
i = i1 + i2
3i2 = 36 ⇒i2 = 12 A
05 E
R
Como i2 = 3 A, a d.d.p. entre os pontos C e B vale:
V
V = R · iP ⇒ iP =
R
VCB = R2 · i2 ⇒ VCB = 10 · 3 ⇒ VCB = 30 V
V
2R
Assim,
VCB = R3 · i3
Logo, iP > iQ.
VP = R · iP
VQ = R · iQ
30 = 15i3
Como iP > iQ ⇒ VP > VQ.
i3 = 2 A
No nó C, tem-se:
i = i2 + i3
2
10
i ⇒ i = 36 A
3
2i1 = 4i2 ⇒ i1 = 2i2 ⇒36 = 2i2 + i2
Q
iQ
Resistência equivalente:
2⋅4
10
∴ Re =
Ω
Re = 2 +
2+ 4
3
V = Re · i ⇒ 120 =
P
As d.d.p.:

R
iP
V = 2R · iQ ⇒ iQ =

Pré-Universitário – Livro 4
5ε
6R
FÍSICA 2
A
R AB
i
R1
i = 3 + 2
i=5A
i
VAC = R1 · i
08 B
i
ε
C
VAC = 5 · 5
Desse modo:
e = VAB ⇒ e = VAC + VCB
e = 25 + 30
e = 55 V
A
R3
10 Ω
R2
R1
R''= 5 Ω
3Ω
6Ω
Série
2Ω
10 Ω
R'= 8 Ω
G
R2
R
2
R1 + R2 = R ⇒ Re =
Corrente iA:
R
2V
⋅ iA ⇒ iA = A
2
R
Interruptor 2 ligado e 1 desligado:
RX
2 volts
(bateria A)
iA
iA
B
De acordo com o esquema, tem-se:
B
R
R
06 D
2Ω
R1
R2
i
Série
Interruptor 1
iA
iA
15 Ω
B
Interruptor 1 ligado e 2 desligado:
i3
i2
VAC = 25 V
5Ω
14R2
14R
= 4 ⇒ R AB =
.
15R
15
4
VA =
12 V
Dessa forma, tem-se uma ponte de Wheatstone equilibrada.
5Ω
R2
8Ω
R1 + R 2 = R
R1
G
10 Ω
No equilíbrio: 5Rx = 8 · 10 ⇒ Rx = 16 W.
R1 + R 2 = R
R2
R1
RX
iB
iB
07 A
Observe a associação e os resistores equivalentes em cada
trecho.
3R
A
Interruptor 2
R'
iB
B
iB
V
(bateria B)
2R
Como R1 + R2 = R ⇒ Re =
3R ⋅ R
3R
R' =
⇒ R' =
3R + R
4
No trecho superior, a resistência será:
3R
7R
R1 = R + R' ⇒ R1 = R +
⇒ R1 =
.
4
4
No trecho inferior, a resistência R2 = 2R.
R
2
R
⋅ iB
2
2 VA
R
⋅2⋅
Se iB = 2iA ⇒ VB =
2
R
VB = 2VA ⇒ VB = 2 ⋅ 2 ⇒ VB = 4 V.
VB = Re ⋅ iB ⇒ VB =
7R
⋅ 2R
R1 ⋅ R2
Entre os pontos A e B ⇒ RAB =
⇒ R AB = 4
7R
R1 + R2
+ 2R
4
Pré-Universitário – Livro 4
3
FÍSICA 2
09 B
O valor de X pode ser determinado considerando:
(20 + X) · 30 · 10–3 = 1,2. Daí, obtém-se X = 20 Ω.
Quando a chave C for fechada, as três resistências de
20 Ω estarão ligadas em paralelo. A resistência equivalente
da ligação em paralelo é calculada a partir de:
1
1
1
1
3
=
+
+
+⇒
=
2
R 20 20 20
⇒
A corrente deve satisfazer:
20 

 20 +  i = 1, 2 ⇒ i = 45 mA.
3
1 3
20
=
⇒R =
Ω
R 20
3
10 D
O circuito está representado a seguir.
A
i1
U = 10 V
A
470 Ω
B
100 Ω
i2
470 Ω
C
120 Ω
Considerando o voltímetro ideal:
10
1
=
A
570 57
U=R·i
10
1
=
A
10 = (470 + 120) · i2 ⇒ i2 =
590 59
10 = (470 + 100) · i1 ⇒ i1 =
1
1
–VA + VB = –470 ·
57
57
⇒
1
1
VA – VC = 470 ·
VA – VC = 470 ·
59
59
VA – VB = 470 ·
⇒
470 470
–
≅ –0,28 V ⇒
59
57
⇒ VB – VC ≅ –0,3 V.
VB – VC =
4
Pré-Universitário – Livro 4