Estudo de Forças de Resistência na Queda de Corpos por Meio de

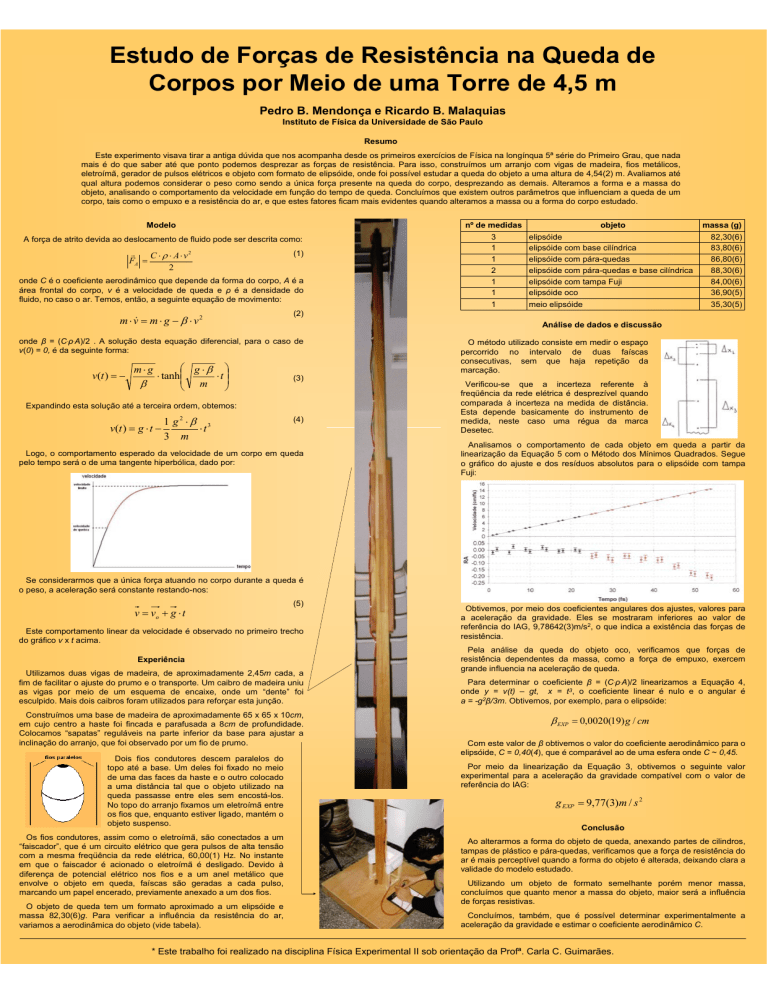
Estudo de Forças de Resistência na Queda de
Corpos por Meio de uma Torre de 4,5 m
Pedro B. Mendonça e Ricardo B. Malaquias
Instituto de Física da Universidade de São Paulo
Resumo
Este experimento visava tirar a antiga dúvida que nos acompanha desde os primeiros exercícios de Física na longínqua 5ª série do Primeiro Grau, que nada
mais é do que saber até que ponto podemos desprezar as forças de resistência. Para isso, construímos um arranjo com vigas de madeira, fios metálicos,
eletroímã, gerador de pulsos elétricos e objeto com formato de elipsóide, onde foi possível estudar a queda do objeto a uma altura de 4,54(2) m. Avaliamos até
qual altura podemos considerar o peso como sendo a única força presente na queda do corpo, desprezando as demais. Alteramos a forma e a massa do
objeto, analisando o comportamento da velocidade em função do tempo de queda. Concluímos que existem outros parâmetros que influenciam a queda de um
corpo, tais como o empuxo e a resistência do ar, e que estes fatores ficam mais evidentes quando alteramos a massa ou a forma do corpo estudado.
Modelo
A força de atrito devida ao deslocamento de fluido pode ser descrita como:
r
C ⋅ ρ ⋅ A ⋅ v2
FA =
2
(1)
onde C é o coeficiente aerodinâmico que depende da forma do corpo, A é a
área frontal do corpo, v é a velocidade de queda e ρ é a densidade do
fluido, no caso o ar. Temos, então, a seguinte equação de movimento:
m ⋅ v& = m ⋅ g − β ⋅ v 2
⎛ g ⋅β ⎞
⋅ tanh⎜⎜
⋅ t ⎟⎟
β
⎠
⎝ m
(3)
Expandindo esta solução até a terceira ordem, obtemos:
1 g2 ⋅β 3
⋅t
3 m
meio elipsóide
massa (g)
82,30(6)
83,80(6)
86,80(6)
88,30(6)
84,00(6)
36,90(5)
35,30(5)
Análise de dados e discussão
m⋅ g
v(t ) = g ⋅ t −
1
objeto
elipsóide
elipsóide com base cilíndrica
elipsóide com pára-quedas
elipsóide com pára-quedas e base cilíndrica
elipsóide com tampa Fuji
elipsóide oco
(2)
onde β = (C.ρ.A)/2 . A solução desta equação diferencial, para o caso de
v(0) = 0, é da seguinte forma:
v(t ) = −
nº de medidas
3
1
1
2
1
1
(4)
Logo, o comportamento esperado da velocidade de um corpo em queda
pelo tempo será o de uma tangente hiperbólica, dado por:
O método utilizado consiste em medir o espaço
percorrido no intervalo de duas faíscas
consecutivas, sem que haja repetição da
marcação.
Verificou-se que a incerteza referente à
freqüência da rede elétrica é desprezível quando
comparada à incerteza na medida de distância.
Esta depende basicamente do instrumento de
medida, neste caso uma régua da marca
Desetec.
Analisamos o comportamento de cada objeto em queda a partir da
linearização da Equação 5 com o Método dos Mínimos Quadrados. Segue
o gráfico do ajuste e dos resíduos absolutos para o elipsóide com tampa
Fuji:
Se considerarmos que a única força atuando no corpo durante a queda é
o peso, a aceleração será constante restando-nos:
v = vo + g ⋅ t
(5)
Este comportamento linear da velocidade é observado no primeiro trecho
do gráfico v x t acima.
Experiência
Utilizamos duas vigas de madeira, de aproximadamente 2,45m cada, a
fim de facilitar o ajuste do prumo e o transporte. Um caibro de madeira uniu
as vigas por meio de um esquema de encaixe, onde um “dente” foi
esculpido. Mais dois caibros foram utilizados para reforçar esta junção.
Construímos uma base de madeira de aproximadamente 65 x 65 x 10cm,
em cujo centro a haste foi fincada e parafusada a 8cm de profundidade.
Colocamos “sapatas” reguláveis na parte inferior da base para ajustar a
inclinação do arranjo, que foi observado por um fio de prumo.
Dois fios condutores descem paralelos do
topo até a base. Um deles foi fixado no meio
de uma das faces da haste e o outro colocado
a uma distância tal que o objeto utilizado na
queda passasse entre eles sem encostá-los.
No topo do arranjo fixamos um eletroímã entre
os fios que, enquanto estiver ligado, mantém o
objeto suspenso.
Os fios condutores, assim como o eletroímã, são conectados a um
“faiscador”, que é um circuito elétrico que gera pulsos de alta tensão
com a mesma freqüência da rede elétrica, 60,00(1) Hz. No instante
em que o faiscador é acionado o eletroímã é desligado. Devido à
diferença de potencial elétrico nos fios e a um anel metálico que
envolve o objeto em queda, faíscas são geradas a cada pulso,
marcando um papel encerado, previamente anexado a um dos fios.
O objeto de queda tem um formato aproximado a um elipsóide e
massa 82,30(6)g. Para verificar a influência da resistência do ar,
variamos a aerodinâmica do objeto (vide tabela).
Obtivemos, por meio dos coeficientes angulares dos ajustes, valores para
a aceleração da gravidade. Eles se mostraram inferiores ao valor de
referência do IAG, 9,78642(3)m/s2, o que indica a existência das forças de
resistência.
Pela análise da queda do objeto oco, verificamos que forças de
resistência dependentes da massa, como a força de empuxo, exercem
grande influencia na aceleração de queda.
Para determinar o coeficiente β = (C.ρ.A)/2 linearizamos a Equação 4,
onde y = v(t) – gt, x = t3, o coeficiente linear é nulo e o angular é
a = -g2β/3m. Obtivemos, por exemplo, para o elipsóide:
β EXP = 0,0020(19) g / cm
Com este valor de β obtivemos o valor do coeficiente aerodinâmico para o
elipsóide, C = 0,40(4), que é comparável ao de uma esfera onde C ~ 0,45.
Por meio da linearização da Equação 3, obtivemos o seguinte valor
experimental para a aceleração da gravidade compatível com o valor de
referência do IAG:
g EXP = 9,77(3)m / s 2
Conclusão
Ao alterarmos a forma do objeto de queda, anexando partes de cilindros,
tampas de plástico e pára-quedas, verificamos que a força de resistência do
ar é mais perceptível quando a forma do objeto é alterada, deixando clara a
validade do modelo estudado.
Utilizando um objeto de formato semelhante porém menor massa,
concluímos que quanto menor a massa do objeto, maior será a influência
de forças resistivas.
Concluímos, também, que é possível determinar experimentalmente a
aceleração da gravidade e estimar o coeficiente aerodinâmico C.
* Este trabalho foi realizado na disciplina Física Experimental II sob orientação da Profª. Carla C. Guimarães.