escalas - aula 3 - geoprocessamento

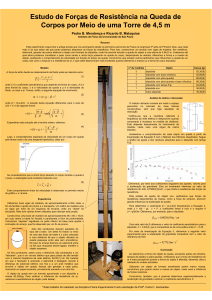
LABORATÓRIO DE GEOPROCESSAMENTO DIDÁTICO
Professora: Selma Regina Aranha Ribeiro
Estagiários: Ricardo Kwiatkowski Silva / Carlos André Batista de Mello
ESCALAS - AULA 3
Precisão Gráfica
É a menor grandeza medida no terreno, capaz de ser representada em um mapa
na mencionada escala. A experiência demonstrou que o menor comprimento
gráfico que se pode representar em um “desenho” é de 1/5 mm ou 0,2mm, sendo
este o erro admissível.
Em função do erro admissível pode-se calcular o erro tolerável para determinada
escala.
•
•
•
E=1/N;
et= erro tolerável em metros;
ea = erro admissível;
et= ea x N= 0,2mm X N= 0,0002 metro x N
O erro tolerável varia na razão direta com o denominador da escala
, portanto quanto menor a escala maior o erro tolerável.
Exemplo.
Escala = 1:1000;
et= 0,0002m x 1000 = 0,2m
Se o menor comprimento que vou utilizar é de 10 metros e a menor medida
que posso representar no desenho (mapa) é de 0,2mm, qual será a escala que
representa este menor comprimento?
et=0,0002;
D= 10 m= 10000 mm
E=d/D= 0,2 mm /10000 mm – 0,2\0,2\10000/0,2 = 1:50.000.
Exercícios:
Escala Gráfica
Talão
escala inteira.
Tabela 1 - escalas
Escala
Em centímetro
No terreno
1:1.000
1cm-1.000cm
10 metros
5 cm
50 metros
1cm-2.000cm
1cm10.000cm
1cm25.000cm
20 metros
100 metros
5 cm
5 cm
100 metros
500 metros
250 metros
5 cm
1.250 metros
1:2.000
1:10.000
1:25.000
Desenhar as escalas gráficas da Tabela 1.
NOÇÕES DE PROJEÇÕES CARTOGRÁFICAS
A TERRA E SUA REPRESENTAÇÃO PLANA
Como a Terra é um corpo rotante, a referência a partir da qual podemos definir sua
geometria é o eixo de rotação.
A superfície física da Terra não admite, por sua complexidade, que se tenha uma
expressão matemática para descrevê-la. Para finalidades práticas, de acordo com o
tipo e a finalidade do trabalho que se deseja realizar, podemos considerar a Terra
como um plano, uma esfera ou um elipsóide de revolução - este é o modelo que
mais se aproxima da forma real da Terra (são simplificações).
N
A(ϕ, λ)
PARALELO – círculo
mínimo // ao equador
ϕ
Q’
EQUADOR - círculo
máximo primário
EIXO DE ROTAÇÃO
(posição média)
Q
λ
MERIDIANO – semi-círculo
máximo secundário
Gr
S
Modelo esférico
Latitude de um ponto (ϕ) é o ângulo que a vertical desse ponto forma com a sua projeção
equatorial. Varia de 0o a 90o, sendo positivo para o norte e negativo para o sul.
Longitude de um ponto (λ) é o ângulo diedro formado entre o meridiano de Greenwich e o
meridiano local. Varia de 0o a 180o, sendo positivo para leste e negativo para oeste.
Temos a Terra dividida em paralelos e meridianos. A rede resultante dos paralelos e
meridianos é conhecida como REDE GEOGRÁFICA. E a interseção do paralelo ϕ
com o meridiano λ é conhecida como coordenadas geográficas (ϕ, λ) - dessa forma
temos um ponto referenciado espacialmente de forma única ou mundial.
Para representarmos a Terra - superfície curva - num plano é necessária utilizarmos
uma projeção cartográfica.
Projeção cartográfica é qualquer arranjo sistemático de meridianos e
paralelos, que representa a superfície curva da esfera ou do elipsóide sobre
um plano.
Como a esfera e o elipsóide não são superfícies desenvolvíveis sobre o plano, as
correspondências não podem ser exatas:
Ν
Y
A(ϕ, λ)
ϕ
PROJEÇÃO
x
Q
Q’
CARTOGRÁFICA
Gr
λ
S
x = f(ϕ, λ)
y = f(ϕ, λ)
SUPERFÍCIE DE REFERÊNCIA
Esfera
Elipsóide
Definidas de acordo com o propósito do
levantamento e do mapeamento.
≠
a (x,y)
y
X
SUPERFÍCIE DE PROJEÇÃO
Plano
Cilindro
Cone
OBS: Plano tangente à Terra num ponto de sua superfície.
Esfera de raio adequado.
Elipsóide de revolução de dimensões adequadas.
→
temos distorções, equivalente a esticar ou rasgar a superfície curva;
→
é necessário uma mudança de escala:
Natureza dos dados espaciais
Dados espaciais caracterizam-se especificamente pelo atributo da localização
geográfica. Há outros fatores importantes inerentes aos dados espaciais, mas a
localização é preponderante. Um objeto qualquer (como uma cidade, a foz de um rio
ou o pico de uma montanha) somente tem sua localização geográfica estabelecida
quando se pode descrevê-lo em relação a outro objeto cuja posição seja
previamente conhecida ou quando se determina sua localização em relação a um
certo sistema de coordenadas.
O estabelecimento de localizações sobre a superfície terrestre sempre foi um dos
objetos de estudo da Geodésia, ciência que se encarrega da determinação da forma
e das dimensões da Terra.
Formas e dimensões da Terra
Geóide: é a superfície equipotencial do campo gravimétrico da terra. É a superfície
de referência para as observações astronômicas. Forma da Terra: a forma de nosso
planeta que tudo é uma questão de ponto de vista. Para os geólogos tem a forma de
um geóide; para a topografia necessitamos realizar adaptações até porque o geói
de não é passível de representação geométrica, assim sendo substituímos
inicialmente o geóide por um elipsóide de revolução, sendo que, a superfície desse
elipsóide muito se aproxima da superfície gerada pelo nível médio dos mares,
supostos tranqüilos e prolongados através dos continentes.
Elipsóide: é uma superfície regular teórica que acompanha aproximadamente o nível
médio dos mares, criada para fins geodésicos e cartográficos.
Elipsóide de referência
Relação entre Superfície física da Terra, geóide, elipsóide:
Esta superfície de nível, chamada geóide não pode ser definida geometricamente,
diferindo do elipsóide de revolução (forma geométrica que dela mais se aproxima)
por ondulações desigualmente distribuídas e devidas à irregularidade de repartições
das massas na crosta terrestre.
Raramente > 30 m
Raramente > 3º
O geóide e o elipsóide de revolução achatado são duas superfícies muito vizinhas,
podendo a segunda ser tomada para superfície de referência relativamente às
medidas de distâncias e ângulos horizontais, que se consideram projetadas naquela
superfície, simplificando-se assim todos os cálculos a serem efetuados com aqueles
elementos.
Já o nivelamento não pode ser referido ao elipsóide, por causa do seu
afastamento em relação ao geóide, e como, além disso, e necessário referir as
altitudes a uma superfície de nível, considera-se neste caso o geóide como
superfície de referência, com a designação habitual de superfície de nível zero.
Equação fundamental da elipse:
Definições: