revisão 2ª fase fuvest – prof.: pica pau

REVISÃO 2ª FASE FUVEST – PROF.: PICA PAU - FÍSICA
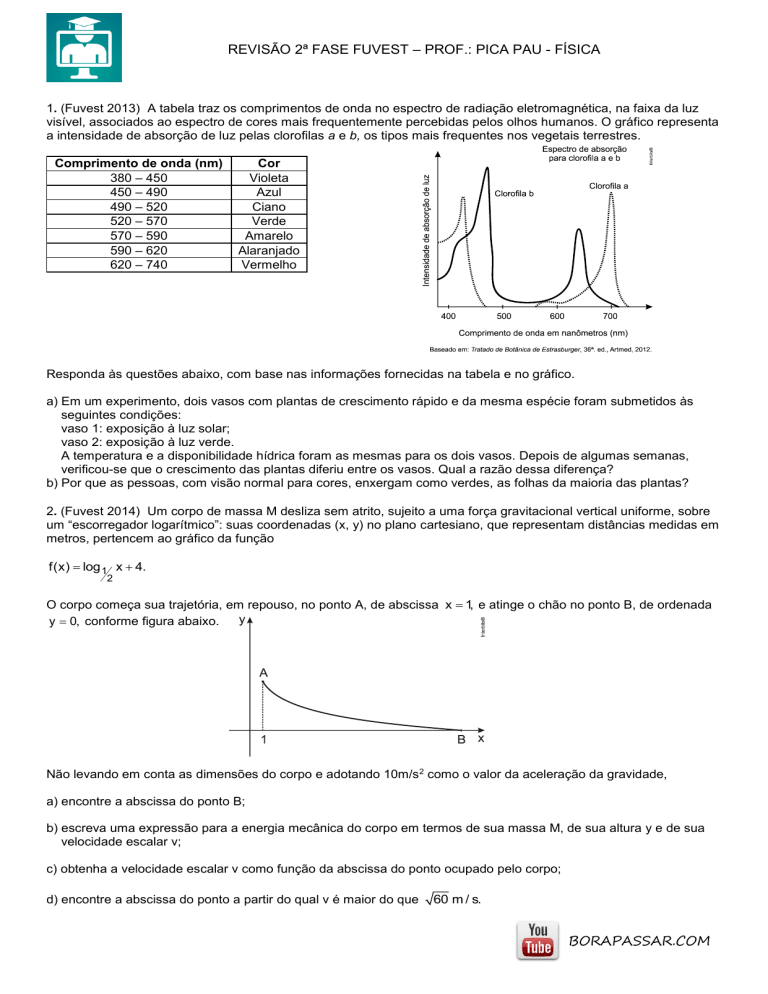
1. (Fuvest 2013) A tabela traz os comprimentos de onda no espectro de radiação eletromagnética, na faixa da luz
visível, associados ao espectro de cores mais frequentemente percebidas pelos olhos humanos. O gráfico representa
a intensidade de absorção de luz pelas clorofilas a e b, os tipos mais frequentes nos vegetais terrestres.
Comprimento de onda (nm)
380 – 450
450 – 490
490 – 520
520 – 570
570 – 590
590 – 620
620 – 740
Cor
Violeta
Azul
Ciano
Verde
Amarelo
Alaranjado
Vermelho
Responda às questões abaixo, com base nas informações fornecidas na tabela e no gráfico.
a) Em um experimento, dois vasos com plantas de crescimento rápido e da mesma espécie foram submetidos às
seguintes condições:
vaso 1: exposição à luz solar;
vaso 2: exposição à luz verde.
A temperatura e a disponibilidade hídrica foram as mesmas para os dois vasos. Depois de algumas semanas,
verificou-se que o crescimento das plantas diferiu entre os vasos. Qual a razão dessa diferença?
b) Por que as pessoas, com visão normal para cores, enxergam como verdes, as folhas da maioria das plantas?
2. (Fuvest 2014) Um corpo de massa M desliza sem atrito, sujeito a uma força gravitacional vertical uniforme, sobre
um “escorregador logarítmico”: suas coordenadas (x, y) no plano cartesiano, que representam distâncias medidas em
metros, pertencem ao gráfico da função
f(x)  log 1 x  4.
2
O corpo começa sua trajetória, em repouso, no ponto A, de abscissa x  1, e atinge o chão no ponto B, de ordenada
y  0, conforme figura abaixo.
Não levando em conta as dimensões do corpo e adotando 10m/s 2 como o valor da aceleração da gravidade,
a) encontre a abscissa do ponto B;
b) escreva uma expressão para a energia mecânica do corpo em termos de sua massa M, de sua altura y e de sua
velocidade escalar v;
c) obtenha a velocidade escalar v como função da abscissa do ponto ocupado pelo corpo;
d) encontre a abscissa do ponto a partir do qual v é maior do que
60 m / s.
BORAPASSAR.COM
REVISÃO 2ª FASE FUVEST – PROF.: PICA PAU - FÍSICA
3. (Fuvest 2014) Duas pequenas esferas, cada uma com massa de 0,2 kg, estão presas nas extremidades de uma
haste rígida, de 10 cm de comprimento, cujo ponto médio está fixo no eixo de um motor que fornece 4 W de potência
mecânica. A figura abaixo ilustra o sistema.
No instante t = 0, o motor é ligado e o sistema, inicialmente em repouso, passa a girar em torno do eixo. Determine
a) a energia cinética total E das esferas em t = 5 s;
b) a velocidade angular ω de cada esfera em t = 5 s;
c) a intensidade F da força entre cada esfera e a haste, em t = 5 s;
d) a aceleração angular média α de cada esfera, entre t = 0 e t = 5 s.
Note e adote:
As massas da haste e do eixo do motor devem ser ignoradas.
Não atuam forças dissipativas no sistema.
4. (Fuvest 1992) Adote: calor específico da água: 1 cal/g.°C
A 10 °C, 100 gotas idênticas de um líquido ocupam um volume de 1,0 cm 3. A 60 °C, o volume ocupado pelo líquido é
de 1,01 cm3. Calcule:
a) A massa de 1 gota de líquido a 10 °C, sabendo-se que sua densidade, a esta temperatura, é de 0,90 g/cm 3.
b) o coeficiente de dilatação volumétrica do líquido.
5. (Fuvest 2004) Durante um jogo de futebol, um chute forte, a partir do chão, lança a bola contra uma parede
próxima. Com auxílio de uma câmera digital, foi possível reconstituir a trajetória da bola, desde o ponto em que ela
atingiu sua altura máxima (ponto A) até o ponto em que bateu na parede (ponto B). As posições de A e B estão
representadas na figura. Após o choque, que é elástico, a bola retorna ao chão e o jogo prossegue.
a) Estime o intervalo de tempo t1, em segundos, que a bola levou para ir do ponto A ao ponto B.
b) Estime o intervalo de tempo t2, em segundos, durante o qual a bola permaneceu no ar, do instante do chute até
atingir o chão após o choque.
c) Represente, em sistema de eixos, em função do tempo, as velocidades horizontal VX e vertical VY da bola em sua
trajetória, do instante do chute inicial até o instante em que atinge o chão, identificando por VX e VY,
respectivamente, cada uma das curvas.
NOTE E ADOTE:
Vy é positivo quando a bola sobe
Vx é positivo quando a bola se move para a direita
BORAPASSAR.COM
REVISÃO 2ª FASE FUVEST – PROF.: PICA PAU - FÍSICA
6. (Fuvest 2007) Recentemente Plutão foi "rebaixado", perdendo sua classificação como planeta. Para avaliar os
efeitos da gravidade em Plutão, considere suas características físicas, comparadas com as da Terra, que estão
apresentadas, com valores aproximados, a seguir.
Massa da Terra (MT) = 500 × Massa de Plutão (MP)
Raio da Terra (RT) = 5 ×Raio de Plutão (RP)
a) Determine o peso, na superfície de Plutão (PP), de uma massa que na superfície da Terra pesa 40N (PT = 40N).
b) Estime a altura máxima H, em metros, que uma bola, lançada verticalmente com velocidade V, atingiria em Plutão.
Na Terra, essa mesma bola, lançada com a mesma velocidade, atinge uma altura hT = 1,5 m.
NOTE E ADOTE:
F = (GMm)/R2
Peso = mg
7. (Fuvest 2010) Segundo uma obra de ficção, o Centro Europeu de Pesquisas Nucleares, CERN, teria
recentemente produzido vários gramas de antimatéria. Sabe-se que, na reação de antimatéria com igual quantidade
de matéria normal, a massa total m é transformada em energia E, de acordo com a equação E = mc 2, onde c e a
velocidade da luz no vácuo.
a) Com base nessas informações, quantos joules de energia seriam produzidos pela reação 1 g de antimatéria com 1
g de matéria?
b) Supondo que a reação matéria-antimatéria ocorra numa fração de segundo (explosão), a quantas “Little Boy” (a
bomba nuclear lançada em Hiroshima, em 6 de agosto de 1945) corresponde a energia produzida nas condições do
item a)?
c) Se a reação matéria-antimatéria pudesse ser controlada e a energia produzida na situação descrita em a) fosse
totalmente convertida em energia elétrica, por quantos meses essa energia poderia suprir as necessidades de uma
pequena cidade que utiliza, em média, 9 MW de potência elétrica?
NOTE E ADOTE:
1 MW =106 W.
A explosão de “Little Boy” produziu 60 × 1012 J (15 quilotons).
1 mês  2,5 × 106 s. velocidade da luz no vácuo, c = 3,0 x 108 m/s.
8. (Fuvest 2010) Um balão de ar quente é constituído de um envelope (parte inflável), cesta para três passageiros,
queimador e tanque de gás. A massa total do balão, com três passageiros e com o envelope vazio, é de 400 kg. O
envelope totalmente inflado tem um volume de 1500 m 3.
a) Que massa de ar M1 caberia no interior do envelope, se totalmente inflado, com pressão igual a pressão
atmosférica local (Patm) e temperatura T = 27 °C?
b) Qual a massa total de ar M2, no interior do envelope, após este ser totalmente inflado com ar quente a uma
temperatura de 127 °C e pressão Patm?
c) Qual a aceleração do balão, com os passageiros, ao ser lançado nas condições dadas no item b) quando a
temperatura externa é T = 27 °C ?
NOTE E ADOTE:
Densidade do ar a 27°C e à pressão atmosférica local = 1,2 kg/m 3.
Aceleração da gravidade na Terra, g = 10 m/s2.
Considere todas as operações realizadas ao nível do mar.
Despreze o empuxo acarretado pelas partes sólidas do balão.
T (K) = T (°C) + 273
BORAPASSAR.COM
REVISÃO 2ª FASE FUVEST – PROF.: PICA PAU - FÍSICA
9. (Fuvest 2013) Um equipamento, como o esquematizado na figura abaixo, foi utilizado por J.J.Thomson, no final do
século XIX, para o estudo de raios catódicos em vácuo. Um feixe fino de elétrons (cada elétron tem massa m e carga
e) com velocidade de módulo v0, na direção horizontal x, atravessa a região entre um par de placas paralelas,
horizontais, de comprimento L. Entre as placas, há um campo elétrico de módulo constante E na direção vertical y.
Após saírem da região entre as placas, os elétrons descrevem uma trajetória retilínea até a tela fluorescente T.
Determine
a) o módulo a da aceleração dos elétrons enquanto estão entre as placas;
b) o intervalo de tempo Δt que os elétrons permanecem entre as placas;
c) o desvio Δy na trajetória dos elétrons, na direção vertical, ao final de seu movimento entre as placas;
d) a componente vertical vy da velocidade dos elétrons ao saírem da região entre as placas.
Note e adote: Ignore os efeitos de borda no campo elétrico; Ignore efeitos gravitacionais.
10. (Fuvest 2013) Em uma aula de laboratório, os alunos determinaram a força eletromotriz å e a resistência interna r
de uma bateria. Para realizar a tarefa, montaram o circuito representado na figura abaixo e, utilizando o voltímetro,
mediram a diferença de potencial V para diferentes valores da resistência R do reostato. A partir dos resultados
obtidos, calcularam a corrente I no reostato e construíram a tabela apresentada logo abaixo.
a) Complete a tabela abaixo com os valores da corrente I.
V(V)
1,14
1,10
1,05
0,96
0,85
R(  )
7,55
4,40
2,62
1,60
0,94
I(A)
0,15
0,40
0,90
b) Utilizando os eixos abaixo, faça o gráfico de V em função de I.
BORAPASSAR.COM
REVISÃO 2ª FASE FUVEST – PROF.: PICA PAU - FÍSICA
c) Determine a força eletromotriz ε e a resistência interna r da bateria.
Note e adote: Um reostato é um resistor de resistência variável; Ignore efeitos resistivos dos fios de ligação do
circuito.
11. (Fuvest 2013) Em uma reação de síntese, induzida por luz vermelha de frequência f igual a 4,3  1014 Hz,
ocorreu a formação de 180 g de glicose. Determine
a) o número N de mols de glicose produzido na reação;
b) a energia E de um fóton de luz vermelha;
c) o número mínimo n de fótons de luz vermelha necessário para a produção de 180 g de glicose;
d) o volume V de oxigênio produzido na reação (CNTP).
Note e adote: 6H2 O  6 CO2  energia  C6 H12 O6  6 O2 ; Massas molares: H (1g/mol), C (12g/mol), O (16g/mol);
Energia do fóton: E  h f; Constante de Planck: h  6,6  1034 J  s; Nessa reação são necessários 2800 kJ de
energia para a formação de um mol de glicose; 1 mol de gás ocupa 22,4 L (CNTP – Condições Normais de
Temperatura e Pressão).
12. (Fuvest 2008) Para carregar um pesado pacote, de massa M = 90 kg, ladeira acima, com velocidade constante,
duas pessoas exercem forças diferentes. O Carregador 1, mais abaixo, exerce uma força F 1 sobre o pacote,
enquanto o Carregador 2, mais acima, exerce uma força F2. No esquema a seguir estão representados, em escala, o
pacote e os pontos C1 e C2, de aplicação das forças, assim como suas direções de ação.
a) Determine, a partir de medições a serem realizadas no esquema a seguir, a razão R = F 1/F2, entre os módulos das
forças exercidas pelos dois carregadores.
b) Determine os valores dos módulos de F1 e F2, em newtons.
c) Indique, no esquema a seguir, com a letra V, a posição em que o Carregador 2 deveria sustentar o pacote para
que as forças exercidas pelos dois carregadores fossem iguais.
NOTE E ADOTE:
A massa do pacote é distribuída uniformemente e, portanto, seu centro de massa, CM, coincide com seu centro
geométrico.
BORAPASSAR.COM
REVISÃO 2ª FASE FUVEST – PROF.: PICA PAU - FÍSICA
13. (Fuvest 2007) Em uma ilha distante, um equipamento eletrônico de monitoramento ambiental, que opera em 12
V e consome 240 W, é mantido ligado 20h por dia. A energia é fornecida por um conjunto de N baterias ideais de 12
V. Essas baterias são carregadas por um gerador a diesel, G, através de uma resistência R de 0,2Ω. Para evitar
interferência no monitoramento, o gerador é ligado durante 4h por dia, no período em que o equipamento permanece
desligado.
Determine
a) a corrente I, em amperes, que alimenta o equipamento eletrônico C.
b) o número mínimo N, de baterias, necessário para manter o sistema, supondo que as baterias armazenem carga de
50 A.h cada uma.
c) a tensão V, em volts, que deve ser fornecida pelo gerador, para carregar as baterias em 4 h.
NOTE E ADOTE
(1 ampere × 1 segundo = 1 coulomb)
O parâmetro usado para caracterizar a carga de uma bateria, produto da corrente pelo tempo, é o ampere . hora
(A.h).
Suponha que a tensão da bateria permaneça constante até o final de sua carga.
14. Em um laboratório de física, estudantes fazem um experimento em que radiação eletromagnética de
comprimento de onda λ = 300 nm incide em uma placa de sódio, provocando a emissão de elétrons.
Os elétrons escapam da placa de sódio com energia cinética máxima Ec = E – W, sendo E a energia
de um fóton da radiação e W a energia mínima necessária para extrair um elétron da placa. A energia
de cada fóton é E = h f, sendo h a constante de Planck e f a frequência da radiação. Determine
a) a frequência f da radiação incidente na placa de sódio;
b) a energia E de um fóton dessa radiação;
c) a energia cinética máxima Ec de um elétron que escapa da placa de sódio;
d) a frequência f0 da radiação eletromagnética, abaixo da qual é impossível haver emissão de
elétrons da placa de sódio.
NOTE E ADOTE
Velocidade da radiação eletromagnética: c = 3 x 108 m/s.
1 nm = 10-9 m.
h = 4 x 10-15 eV.s.
W (sódio) = 2,3 eV.
1 eV = 1,6 x 10-19 J.
BORAPASSAR.COM
REVISÃO 2ª FASE FUVEST – PROF.: PICA PAU - FÍSICA
Gabarito:
Resposta da questão 1:
[Resposta do ponto de vista da disciplina de Biologia]
a) No vaso 1, a planta cresce normalmente, pois consegue absorver os comprimentos de onda equivalentes ao azul e
ao vermelho. Esses comprimentos de onda tornam a taxa de fotossíntese mais eficiente. A planta do vaso 2 reflete
a radiação verde e não consegue crescer devido à ineficiência de sua taxa fotossintética.
[Resposta do ponto de vista da disciplina de Física]
b) A cor de um objeto é a mesma cor da radiação que ele mais difunde (reflete). Portanto, se as pessoas com visão
normal enxergam as folhas como verdes, é porque elas refletem com maior intensidade a radiação correspondente à
luz verde.
Resposta da questão 2:
a) Quando x  xB  yB  0.
Assim:
 1
log 1 x  4  0  log 1 x  4   
2
2
2
4
 x  x  24 
x  16 unidades de comprimento.
b) Usando a expressão da Energia Mecânica:
Emec  Ecin  Epot
 Emec 
 v2

M v2
 M g y  Emec  M 
 g y 
 2

2


 v2

Emec  M 
 10 y  unidades de energia.
 2



c) Como o corpo parte do repouso em x = 1, temos v0 = 0.
Na expressão dada, para x = 1, temos:
y  log 1 1  4  0  4  y  4.
2
Aplicando esses dados na expressão obtida no anterior:
 v2

 02

Emec  M 
 10 y   Emec  M 
 10  4  
 2

 2





Emec  40 M .
Pela conservação da Energia Mecânica:
 2


v
v2
v2
M
 10  log 1 x  4    40 M 
 40  10 log 1 x  40 
 -10 log 1 x 
 2


2
2
2
2
 2


v
-20 log 1 x .
2
Caso queiramos eliminar o sinal (–) do radicando, podemos mudar o logaritmo para a base 2:
BORAPASSAR.COM
REVISÃO 2ª FASE FUVEST – PROF.: PICA PAU - FÍSICA
log 1 x 
2
log2 x log2 x

1
1
log2
2
 log 1 x  log2 x.
2
Assim:
v
20 log2 x unidades de velocidade.
Resposta da questão 3:
a) Dados: P = 4 W; Δt  5 s.
E  P Δt  4  5  E  20 J.
b) Dados: m = 0,2 kg; R  5 cm  5  102 m.
A energia cinética das duas esferas é:
m v2
2
 m  ω R   E  m ω2 R2 
2
1 E
1
20 100
ω


100 

2
R m 5  10
0,2
5
E2
ω  200 rad/s.
c) A aceleração (a) da esfera tem duas componentes: tangencial (aT ) e centrípeta (aC ).
- Componente tangencial:
v  aT t  ω R  aT t  aT 
ω R 200  5  102

t
5
 aT  0,2 m/s2.
- Componente centrípeta:

aC  ω2 R  2  102

2
 5  102  4  104  5  102  aC  2  103 m/s2.
Comparando os valores obtidos, a componente tangencial tem intensidade desprezível. Então a intensidade da
resultante é igual à da componente centrípeta.
aT  aC  a  aC  2  103 m / s2 .
Aplicando o Princípio Fundamental da Dinâmica:
Fres  m a  0,2  2  103  0,4  103 
Fres  400 N.
d) α 
aT
2

 0,4  102  α  40 rad/s2 .
2
R
5  10
Resposta da questão 4:
a) 9,0 . 10–3 g.
b) 2,0 . 10-4 °C–1.
a) Dados: ρ = 0,9 g/cm3; V = 1 cm3; M = 100 m.
ρ
M
V
 M  ρ V  100 m  ρ V  m 
ρ V 0,9  1
9


100
100 1000

m  9  103 g.
b) Dados: V0 = 1 cm3; V = 1,01 cm3; θ0 = 10 °C; θ = 60 °C.
BORAPASSAR.COM
REVISÃO 2ª FASE FUVEST – PROF.: PICA PAU - FÍSICA
ΔV  V0 γ Δθ  γ 
V  V0
1,01  1
0,01
1
1





V0  θ  θ0  1  60  10 
50
5000 5  103
γ  2  104 C1.
Resposta da questão 5:
a) Todo lançamento oblíquo, a partir do ponto mais alto, torna-se um lançamento horizontal, assim como todo
lançamento vertical para cima, a partir do ponto mais alto, torna-se uma queda livre.
A partir do ponto A, temos um lançamento horizontal. Até o ponto B a bola cai yB e avança xB = 6 m.
yB  5  4,2  yB  0,8 m.
Adotando origem no ponto A e orientando o eixo y verticalmente para baixo, temos:
y 
B
1
gt
2
2
1
 t 
1
2y

g
B
2  0,8 
10
 0,16 
t  0,4 s.
1
b) Usando o mesmo a mesma expressão do item anterior, até atingir o solo, y = h = 5 m. Assim, calculamos o tempo
de descida (td).
td 
2 h

g
2 5
10
 t d  1 s.
Como o solo é plano e horizontal, o tempo de subida (ts) é igual ao de descida. Então, o tempo total (t2) é:
t 2  t s  t d  1  1  t 2  2 s.
c) No eixo x, o movimento é uniforme. De A até B, a bola avança  x  6m no sentido positivo e gasta t1 = 0,4 s. No
ponto B, a componente horizontal da velocidade inverte o sentido.
Assim:
x
6
Vx 

 Vx  15 m / s.
t 2 0,4
No eixo y, o movimento é uniformemente variado e o tempo de subida é ts = 1 s. No ponto mais alto, a
componente vertical da velocidade é nula.
Assim:
Vy  V0y  g t s  0  V0y  10 1  V0y  10 m / s.
Em t = 2 s:
Vy  V0y  g t s  Vy  10  10  2   Vy  10 m / s.
Resposta da questão 6:
a) A aceleração da gravidade na superfície de qualquer astro é dada pela expressão:
BORAPASSAR.COM
REVISÃO 2ª FASE FUVEST – PROF.: PICA PAU - FÍSICA
g
GM
R2
Onde: M  massa do astro; R  raio do astro
M
G T
GMP
1 GMT
1
gP  2  5002 
. 2 
gT
20 RT
20
RP
 RT 
 5 


Como a gravidade em Plutão é vinte vezes menor que a terrestre, os corpos pesam 20 vezes menos.
PT  40N  PP  2,0N
b) Em um lançamento vertical:
1
V2
mgh  mV 2  h 
2
2g
Como a altura é inversamente proporcional a “g” e como a gravidade em plutão é 20 vezes menor que a terrestre,
a altura alcançada será 20 vezes maior.
HP  20HT  30m
Resposta da questão 7:
PRIMEIRA QUEDA
a) O movimento na vertical é um MUV:
1
S  gt 2  3,2  5t 2  t  0,8s
2
O movimento na horizontal é uniforme:
S  V0 .t  1,6  V0  0,8  V0  2,0m / s
MOVIMENTO AB
b) O movimento na vertical é um MUV:
1
S  gt 2  1,8  5t 2  t  0,6s
2
O movimento na horizontal é uniforme:
S  V0 .t  D  2  (2  0,6)  D  2,4m
c) O movimento na vertical é um MUV: V  VA  at  0  VA  10  0,6  VA  6,0m / s .
Resposta da questão 8:
Dados:
m = 2 g = 2  10–3 kg; ELB = 60  1012 J = 6  1013 J; c = 3  108 m/s; 1 mês = 2,5  106 s.
a) E = m c2 = 2  10–3  (3  108)2 = 2  10–3  9  1016 
E = 1,8  1014 J.
b) Sendo n a quantidade de bombas “Little Boy”, temos:
n=
E
1,8  1014


ELB
6  1013
n = 3 (Little Boys).
BORAPASSAR.COM
REVISÃO 2ª FASE FUVEST – PROF.: PICA PAU - FÍSICA
E
E 1,8  1014
 t  
 2  107 s.
t
P
9  106
c) P 
Transformando em meses:

t = 8 meses.
Resposta da questão 9:
a)
A figura mostra as forças que agem sobre um íon: a força elétrica no mesmo sentido do campo elétrico, pois os
íons são positivos; pela regra da mão direita encontramos a força magnética, oposta à força elétrica. Para o íons
que passam pela fenda F2 essas forças se equilibram. Então:
Fmag  Felet  q v B1  q E 
v
E
.
B1
'
) devida a B2 exerce o papel de resultante centrípeta. Então:
b) A força magnética (Fmag
'

Rcent = Fmag

m v2
m B2 R
E
 q v B2  
. Substituindo o v pela expressão encontrada no item anterior  v 
,
R
q
v
B1 

vem:
m B2 R


q E
B1
m B1 B2

R.
q
E
c) Dado: B'2 = 2 B2.
Isolando R na expressão obtida no item anterior, obtemos:
R
mE
.
q B1 B2
O novo raio, R’ é, então:
R' 
mE
mE
.
 R' 
q B1 2 B2
2 q B1 B2
A razão entre esses raios é:
BORAPASSAR.COM
REVISÃO 2ª FASE FUVEST – PROF.: PICA PAU - FÍSICA
q B1 B2
mE
R'
R' 1



 
R 2 q B1 B2
mE
R 2
R' 
R
.
2
Resposta da questão 10:
a) Dados: dar = 1,2 kg/m3; V = 1.500 m3.
M
dar  1  M1  dar V  1,2 (1.500)  M1 = 1.800 kg.
V
b) Dados: T1 = 27 °C = 300 K e T2 = 127°C = 400 K.
Sendo M a massa molar do ar, aplicando a equação de Clapeyron, vem:
M
Patm V  1 RT1 (equação I)
M
M2
Patm V 
RT2 (equação II)
M
Dividindo (I) por (II), obtemos:
MT
M T 1.800 (300)
1 = 1 1  M1T1  M2 T2  M2  1 1 
 M2 = 1.350 kg.
M2 T2
T2
400
c) Dados: massa total: m = mpassag + M2 = 400 + 1.350 = 1.750 kg; dar = 1,2 kg/m3.
As forças que agem no balão são o peso e o empuxo.
Aplicando o princípio fundamental da dinâmica, temos:
E – P = m a  dar g V – m g = m a  (1,2) (10) (1.500) – 1.750 (10) = 1.750 a  18.000 – 17.500 = 1.750 a 
500
 a = 0,29 m/s2.
a
1.750
Resposta da questão 11:
a) Dados: P = 8 MW = 8  106 W; m = 500 t = 5 105 kg; v0 = 0; v = 288 km/h = 80 m/s.
O trabalho realizado pela força impulsora dos motores pode ser calculado pelo teorema da energia cinética.
m v 2 m v 02 5  105  802
WFv  Ecin 


 16  108 J.
motor
2
2
2
Mas:
WFv
WFv
16  108
motor
motor
 t = 200 s.
P
 t 

t
P
8  106
b) Dados: m = 500 t = 5  105 kg; v0 = 0; v = 288 km/h = 80 m/s; r = 5 km = 5  103 m; N = 80 rodas.
Se a velocidade é constante, a força resultante na direção horizontal é estritamente radial. Ou seja, essa força é a
resultante centrípeta. A força atuante em cada roda é:
m v2
2
5
2
RCent
r  m v  5  10  80 
Froda 

N
N
Nr
80  5  103
Froda = 8.000 N.
c) Dados: m = 500 t = 5  106 kg; v0 = 0; v = 288 km/h = 80 m/s; P = 8  106 W.
Nesse item há um deslize da banca examinadora, pois não foi especificado se a frenagem ocorre em um trecho
retilíneo ou curvilíneo.
Suponhamos que seja em um trecho retilíneo. Sendo a o módulo dessa aceleração, da expressão da potência
instantânea, vem:
BORAPASSAR.COM
REVISÃO 2ª FASE FUVEST – PROF.: PICA PAU - FÍSICA
P = Fv  P = mav  a 
P
8  106
 a = 0,2 m/s2.

m v 5  105  80
Resposta da questão 12:
Dados: Δx  L; q  e  q  e .
a) A força resultante sobre o elétron é a força elétrica:
Fres  Felet  m a | q | E  m a | e | E 
|e|E
.
m
b) Como a força elétrica atua apenas no eixo y, no eixo x a componente da velocidade permanece constante, igual a
v0. Então:
L
Δx  v 0 Δt  L  v 0 Δt  Δt 
.
v0
c) No eixo y, o movimento é uniformemente variado. Sendo v0y = 0:
a
Δy 
1 2
1 e E L 
a t  Δy 
 
2
2 m  v0 
2
 Δy 
e E L2
.
2 m v02
d) Aplicando a função horária da velocidade no eixo y, com voy = 0:
vy  a t  vy 
eE L

m v0
 vy 
eE L
m v0
.
Resposta da questão 13:
a) Aplicando a 1ª Lei de Ohm na 2ª e 4ª linhas:
1,1

I2 
 0,25 A.

4,4
V 
V R I  I

0,96
R 
I 
 0,60 A.
 4
1,6
V(V)
1,14
1,10
1,05
0,96
0,85
R(  )
7,55
4,40
2,62
1,60
0,94
I(A)
0,15
0,25
0,40
0,60
0,90
b) Substituindo os valores da tabela do item anterior:
BORAPASSAR.COM
REVISÃO 2ª FASE FUVEST – PROF.: PICA PAU - FÍSICA
Obs.: no eixo das tensões, os valores começam a partir de V = 0,7 V, por isso a reta não cruza o eixo das
correntes no valor da corrente de curto circuito.
c) Substituindo os dois primeiros valores de V e de I da tabela na equação do gerador e subtraindo membro a
membro as duas equações:
1,14  ε  r  0,15 

0,04
V  ε  r I 1,10 ε  r  0,25  
 r
 r  0,4 Ω.
0,1


0  0,10 r
 0,04
1,14  ε   0,4  0,15 
 ε  1,14  0,06  ε  1,2 V.
Obs.: A equação dessa bateria é:
V  1,2  0,4 I.
Para V = 0,7 V:
1,2  0,7
0,7  1,2  0,4 I  I 
 i  1,25 A.
0,4
Esse é o valor em que a linha do gráfico corta o eixo das correntes, como assinalado no gráfico do item anterior.
Resposta da questão 14:
Dados: M = 6  1024 kg; m = 1016 kg; v0 = 30 km/s = 3  104 m/s; 1 megaton = 4  1015 J.
a) Pi  m v0  1016  3  104  Pi  3  1020 kg  m / s.


2
16
4
m v 02 10  3  10

 Ec  4,5  1024 J.
b) Ec 
2
2
c) Trata-se de um choque inelástico. A massa do meteoro é desprezível em relação à massa da Terra, por isso,
depois do choque, a massa do sistema é apenas a massa da Terra, pois:
6  1024  1016  6,00000001 1024  6  1024.
Pela Conservação da Quantidade de movimento:
Antes
QSist
 QDepois
 m v o  M  m  v  v 
Sist
m v 0 3  1020

 5  10 5 m / s 
24
M
6  10
v  0.
O choque do meteoro com a Terra praticamente não altera a velocidade da Terra.
d) Pela resposta do item anterior, conclui-se que toda energia cinética do meteoro é dissipada na colisão. Passando
para megaton:
4  1015 J  1 megaton
4,5  1024

 Edissip 


24
4  1015
 Edissip
4,5  10
Edissip  1,125  109 megaton.
BORAPASSAR.COM
REVISÃO 2ª FASE FUVEST – PROF.: PICA PAU - FÍSICA
Resposta da questão 15:
[Resposta do ponto de vista da disciplina de Química]
a) De acordo com o enunciado ocorreu a formação de 180 g de glicose e este valor corresponde a um mol de glicose
(C6H12O6  6  12  12  1  6  16  180).
b) Como a energia do fóton é dada por E  h f , onde h  6,6  1034 J  s .
Na reação de síntese, induzida por luz vermelha de frequência f igual a 4,3  1014 Hz, então:
E  h f
E  6,6  1034 J  s  4,3  1014 s1  28,38  1020  2,84  1019 J
E  2,8  1019 J (um fóton)
c) Nessa reação são necessários 2800 kJ (2800 kJ  2,8  106 J) de energia para a formação de um mol de glicose,
então:
2,8  10 19 J
2,8  10 J
6
n  10
25
1 fóton
n
fótons
d) 6H2O  6CO2  energia  C6H12O6  6O2 ; CNTP.
1 mol (O2 )
22,4 L
6mol (O2 )
V
V  134,4 L
[Resposta do ponto de vista da disciplina de Física]
a) Química.
b) Dado: h  6,6  10–34 J  s; f  4,3  1014 Hz.
Aplicando esses valores na equação dada:
E  h f  6,6  1034  4,3  1014  E  2,8  1019 J.
c) Dado: Glicose  C6H12O6 ; H (1g/mol), C (12g/mol), O (16g/mol); E = 2.800 kJ/mol = 2,8  106 J/mol.
A massa molar da glicose é:
M  (6  12)  (12  1)  (6  16)  180 g.
Calculando o número n de fótons para produzir 1 mol de glicose ou 180 g.
nE  2.800  103  n 
2.800  103
2,8  10
19
 n  1025 fótons.
d) Dado: nas CNTP, o volume ocupado por um mol de gás é 22,4 L.
A reação dada mostra que são produzidos 1 mol de glicose e 6 mols de O 2. Assim, o volume produzido de O2 na
reação é:
V  6  22,4  V  134,4 L.
Resposta da questão 16:
a) Observe as forças agindo no corpo.
BORAPASSAR.COM
REVISÃO 2ª FASE FUVEST – PROF.: PICA PAU - FÍSICA
Para haver equilíbrio é necessário que:
M  0
Determinando os momentos das forças em relação ao centro de massa, vem:
F
F1  4d  F2  8d  0  F1  2F2  R  1  2
F2
b) Para haver equilíbrio a resultante das forças deve ser nula.
Isto é: F1  F2  P  0  2F2  F2  900  F2  300N
Como F1  2F2  F1  600N
c) Para que as forças fossem iguais os braços de alavanca deveriam ser iguais. Observe a figura.
BORAPASSAR.COM
REVISÃO 2ª FASE FUVEST – PROF.: PICA PAU - FÍSICA
Resposta da questão 17:
a) P  V.i  240  12i  i  20A
b) Carga de cada bateria
50A.h  50  3600  18.000C
Carga total para 20h de funcionamento
Q
Q
i
 20 
 Q  144.000C
t
20  3600
144.000
N
 8 baterias
18.000
c) Gerador
Ig 
Vg  12 Q
Vg  12 144.000



 Vg  12  2  Vg  14V
R
t
0,2
4  3600
BORAPASSAR.COM