3ª Ficha Global de Física 12º ano

3ª Ficha Global de Física 12º ano
Todos os cálculos devem ser apresentados de modo claro e sucinto
Note: 1º - as figuras não estão desenhadas a escala;
Adopte quando necessário:
G
g = 10 m.s−2
G = 6,67 × 10-11 N.m2.kg −2
RTerra = 6,37 ×106 m
MTerra = 5,98 × 1024 kg
ρ água = 1,0 × 10 3 kg.m -3
k0 = 9,0 × 109 N.m2 C-2
km0 =
µ0
= 1,0 × 10-7 H.m-1
4π
|qe− |= 1,6 × 10−19 C
mprotão = 1,67 × 10− 27 kg
melectrão = 9,12 × 10− 31 kg
sen(30o) = 0,50
cos(300) = 0,87
NetProf
Página 1 de 8
Grupo I
Algumas das questões a seguir foram retiradas de exames de acesso a universidades brasileiras. Quando for o caso, estará indicado entre
parênteses esse exame
1. (FUVEST 2002) Dois pequenos discos, de massas iguais, são lançados sobre uma superfície plana e horizontal,
sem atrito, com velocidades de módulos iguais. A figura a seguir regista a posição dos discos, vistos de cima, em
intervalos de tempo sucessivos e iguais, antes de colidirem, próximo ao ponto P. Dentre as possibilidades
representadas, aquela que pode corresponder às posições dos discos, em instantes sucessivos, após a colisão, é:
A
B
C
D
E
2. (FUVEST 2002) Um avião, com massa M = 90 toneladas, para que esteja em equilíbrio em voo, deve manter o
seu centro de gravidade sobre a linha vertical CG, que dista 16 m do eixo da roda dianteira e 4,0 m do eixo das
rodas traseiras, como na figura a seguir. Para estudar a distribuição de massas do avião, em solo, três balanças são
colocadas sob as rodas de aterragem. A balança sob a roda dianteira indica MD e cada uma das que estão sob as
rodas traseiras indica MT.
NetProf
Página 2 de 8
Uma distribuição de massas, compatível com o equilíbrio do avião em voo, poderia resultar em indicações das
balanças, em toneladas, correspondendo aproximadamente a:
A MD = 0 e MT = 45
B MD = 10 e MT = 40
C MD = 18 e MT = 36
D MD = 30 e MT = 30
E MD = 72 e MT = 9
3. Na figura a seguir está representado um balão contendo um gás de densidade ρGás, menor que a densidade do ar
ρAr, preso a um fio. O balão está completamente imerso no ar. Considere a massa do material de que é feito o balão
desprezável e seja m a massa do gás. A intensidade da força de tensão no fio é dada por:
A T = mg (ρ Ar − ρGás )
 ρ Ar − ρGás 

 ρGás 
 ρ − ρGás 
C T = mg  Ar

 ρ Ar

B T = mg 
 ρ Ar − ρGás 

 ρGás 
E T = mg ρGás
D T = m
NetProf
Página 3 de 8
4. Um objecto de massa M, inicialmente em repouso, desce um plano inclinado em movimento uniformemente
acelerado. Seja µc o coeficiente de atrito cinético entre o corpo e a superfície de apoio. A módulo da aceleração que
o corpo adquire no movimento é dada por:
A a = gsen(θ)
B a = g µ c sen(θ)
C a = g [ cos(θ) − µ c sen(θ)]
D a = g [ sen(θ) − µ c cos(θ)]
E a=
g
[ cos(θ) − sen(θ)]
µc
G
5. Uma partícula de carga positiva e massa m, penetra numa região onde actua um campo magnético B conforme a
figura a seguir:
O raio da trajectória descrita pela partícula ao penetrar nesse campo é dado por:
A R=
mv
qB
B R = mvqB
mv 2
B
mv 2
D R=
qB
C R=
E R=
qv 2
B
m
NetProf
Página 4 de 8
6. Três fios condutores paralelos, rectos e muito longos são colocados verticalmente conforme mostra figura a
seguir.
As correntes eléctricas que percorrem os fios têm intensidades iB = iC = 2iA. Podemos afirmar que:
A Os fios A e B se atraem.
B Os fios B e C se atraem.
C Os fios A e B se afastam.
D A força resultante em cada fio é nula.
E A força resultante em A é nula.
Grupo II
1. Três partículas ocupam, num dado referencial, as posições mostrada na figura a seguir num instante t. As massas
das partículas são m1= 2,0 kg, m2= 2,0 kg e m3= 4,0 kg. As suas velocidades nesse instante são:
G
G
G
G
G
G
G
v1 = 2, 0i (m.s −1 ) v2 = −3, 0 j (m.s −1 ) e v3 = 2, 0i + 2, 0 j (m.s −1 )
NetProf
Página 5 de 8
1.1. Determine a posição do centro de massa do sistema.
1.2. Determine a velocidade do centro de massa do sistema nesse instante
1.3. Determine a posição da partícula 1 em relação ao referencial do centro de massa
1.4. Determine o momento linear do sistema em relação ao referencial do centro de massa
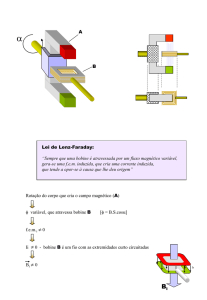
2. (40 pontos) (FUVEST 2004) Com auxílio de uma pequena bússola e de uma bobine, é possível construir um
instrumento para medir correntes eléctricas. Para isso, a bobine é posicionada de tal forma que o seu eixo coincida
com a direcção Leste-Oeste da bússola, sendo esta colocada em uma região em que o campo magnético B da
bobine pode ser considerado uniforme e dirigido para Leste. Assim, quando a corrente que percorre a bobine é
igual a zero, a agulha da bússola aponta para o Norte. À medida em que, ao passar pela bobine, a corrente I varia, a
agulha da bússola se move, apontando em diferentes direcções, identificadas por θ, ângulo que a agulha faz com a
direcção Norte. Os terminais A e B são inseridos convenientemente no circuito onde se quer medir a corrente. Uma
medida inicial de calibração indica que, para θ0 = 45°, a corrente I0 = 2 A.
Adopte:
•A componente horizontal do campo magnético da Terra, BT ≈ 0,2 gauss.
•O campo magnético B produzido por esta bobine, quando percorrida por uma corrente I, é dado por B = k I, em
que k é uma constante de proporcionalidade.
•A constante k = µ0 N, em que µ0 é uma constante e N, o número de espiras por unidade de comprimento da
bobina.
Para essa montagem:
2.1 Determine a constante k de proporcionalidade entre B e I, expressa em gauss por ampere.
NetProf
Página 6 de 8
2.2 Estime o valor da corrente I1,em amperes, quando a agulha indicar a direcção θ1,representada na figura a seguir.
Utilize, para isso, uma construção gráfica.
(Cada quadrícula 0,5 unidades)
2.3 Passe o esquema representado na figura a cima para a sua folha de respostas. Indique, nesse esquema, a nova
direcção θ2 que a bússola apontaria, para essa mesma corrente I1, caso a bobina passasse a ter seu número N de
espiras duplicado, sem alterar seu comprimento.
3. (45 pontos) (FUVEST 2003) Duas pequenas esferas metálicas, A e B, são mantidas em potenciais electrostáticos
constantes, respectivamente, positivo e negativo. As linhas cheias do gráfico representam as intersecções, com o
plano do papel, das superfícies equipotenciais esféricas geradas por A, quando não há outros objectos nas
proximidades. De forma análoga, as linhas tracejadas representam as intersecções com o plano do papel, das
superfícies equipotenciais geradas por B. Os valores dos potenciais eléctricos dessas superfícies estão indicados no
gráfico. As questões se referem à situação em que A e B estão na presença uma da outra, nas posições indicadas no
gráfico, com seus centros no plano do papel.
Uma esfera com carga Q produz, fora dela, a uma distância r do seu centro, um potencial V e um campo eléctrico
de módulo E, dados pelas expressões:
NetProf
Página 7 de 8
V =k
Q
Q V
e E=k 2 =
r
r
r
3.1 Trace em toda a extensão do gráfico, a linha de potencial V = 0, quando as duas esferas estão nas posições
indicadas. Identifique claramente essa linha por V = 0.
3.2 Determine, em volt/metro, utilizando dados do gráfico, os módulos dos campos eléctricos EPA e EPB criados, no
ponto P, respectivamente, pelas esferas A e B.
3.3 Represente, em uma escala conveniente, no gráfico, com origem no ponto P, os vectores EPA, EPB e o vector
campo eléctrico EP resultante em P. Determine, a partir desta construção gráfica, o módulo de EP, em volt/metro.
3.4 Estime o módulo do valor do trabalho, em joules, realizado quando uma pequena carga q = 2,0 nC é levada do
ponto P ao ponto S, indicados no gráfico
NetProf
Página 8 de 8