Medidas elétricas, Lei de Ohm, Lei de Kirchhoff, capacitores e

1
Experimental - Eletricidade e Magnetismo
Prof. Paulo Sérgio Moscon
Universidade Federal do Espírito Santo, Brasil
Outubro 13/10/2010
Parte I
Medidas elétricas, Lei de Ohm, Lei de
Kirchhoff, capacitores e circuitos RC
Resumo
Serão abordados os seguintes assuntos:
1. Lei de Ohm / resistividade
2. Leis de Kirchhoff
3. Capacitores
4. Associações de capacitores em Série e Paralelo
5. Circuito RC
2
6. Experimento de Oersted
Materiais utilizados
Resistores e capacitores diversos, matriz de contato (protoboard), fios para contato, cronômetro digital, multímetros, fontes de voltagem, fontes de corrente e tabela de cores para leitura de resistência.
3
1 Resistores - Lei de Ohm/Resistividade
Este experimento tem como objetivos estudar a lei de Ohm a partir de medidas de corrente elétrica
sobre resistores ôhmicos e obter a resistividade dos diferentes materiais.
1.1 Teoria
1.1.1
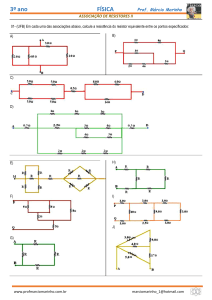
Associação de resistores
Um circuito com n resistores ligados em série funciona como um circuito composto por um único
resistor com resistência equivalente R∗ dado por
R∗ =
X
Rn ,
para n = 1, 2, 3, ..., n
(1)
n
A demonstração da Equação 1 está detalhada na Figura 1
Um procedimento análogo para uma associação de resistores em paralelo (detalhada na Fig. 2) nos
leva à uma resistência equivalente de
1 X 1
=
.
R∗
R
n
n
1.1.2
(2)
Resistividade
Na seção 1.1.1 tratamos da resistência total entre as extremidades de um material, não importanto a
geometria do material resistivo. Nesta seção vamos mostrar que a resistência de um material depende
além do características intrínsecas determinadas por sua composição atômica (resistividade), também
de suas dimensões. Por exemplo, um material mais fino oferece maior resistência à passagem de uma
corrente elétrica se comparado com o mesmo material mais largo. Analogamente, quando maior o
comprimento de um material, maior a dificuldade encontrada pela corrente elétrica para atravessá-lo.
4
Figura 1: Resistência equivalente (R*) de uma associação de resistores em série.
Figura 2: Resistência equivalente (R*) de uma associação de resistores em paralelo.
5
Demostração
Para um material ôhmico, a corrente elétrica que atravessa uma unidade de área transversal (densidade
~ é proporcional ao campo elétrico na região considerada, ou seja, J~ ∝ E.
~ Desta forma
de corrente J)
podemos escrever
~
J~ = σE,
(3)
onde, a constante de proporcionalidade é definida como condutividade elétrica σ. Se σ representa a
condutividade, é natural definirmos
1
σ
≡ ρ como a resistividade elétrica. Temos então que
~
E~ = ρ J.
(4)
Segue então a demonstração simples apresentada na Fig. 3, onde mostramos que a resistência R é
dada por
R=
ρ
l.
A
(5)
6
Figura 3: Obtenção da relação entre resistência e a resistividade de um material com comprimento l e área
transversal A.
1.2 Experimentos
1.2.1
Associação de resistores
No laboratório de física temos uma placa de protoboard com diferentes fios resistivos esticados em
forma de zig-zag, como representamos na Fig. 4. Nesta experimento procede-se da seguinte forma:
1. Mede-se separadamente a resistência de cada fio.
2. Com os valores acima, calcula-se teoricamente a resistência equivalente com os resistores ligados em série e com os resistores ligados em paralelo.
3. Mede-se a resistência das configurações em série e em paralelo e compara-se com o valor
teórico obtido.
4. Analisar os resultados
7
Figura 4: Configuração dos fios resistivos na placa de protoboard
1.2.2
Obtenção da resistividade de diferentes materiais, através do coeficiente angular da curva R(l).
No laboratório de física experimental temos uma placa de protoboard com diferentes fios resistivos
esticados em forma de zig-zag, como representamos na Fig.4.
Com o auxílio de um multímetro pré-definido para medida de resistência elétrica R, medir a resistência nos pontos A, B, C e D; todos com relação ao ponto 0.
Com o auxílio de um paquímetro medir o diâmetro de cada fio, com o objetivo de se obter a área
transversal A.
Com o auxílio de uma régua, medir os comprimentos OA, OB, OC e OD.
Traçar o gráfico de R em função do comprimento l e obter a resistividade através do coeficiente
angular deste gráfico.
8
1.2.3
Obtenção da resistividade de algum material (a ser definido durante o experimento) através da
curva do potencial V em função da corrente i.
Através das relações V = Ri e R = ρl/A, temos que
V=
ρl
i.
A
(6)
Desta forma, e possível, para um material ôhmico, determinarmos a resistividade (se conhecidos o
comprimento e a área transversal) através do coeficiente angular da reta V(i).
OBS: Elaborar uma tabela com uma quantidade de dados adequadamente (coerentemente) divididos
entre zero e o valor máximo de corrente definida durante o experimento (a ser definida pelo professor
e/ou pelo monitor). Neste experimento deve-se utilizar uma fonte de voltagem com limitador superior
de corrente. Caso a fonte com limitador de corrente não esteja disponível, é possível utilizar uma fonte
comun de voltagem; neste caso, o resistor deve ser escolhido de forma a suportar a voltagem máxima
utilizada (resistores de fio são mais adequados).
2 Circuito RC
3 O Campo Magnético
Neste experimento vamos gerar um campo magnético conhecido através de um solenóide comprido.
Lembremos que o campo dentro de um solenóide infinitamente comprido é
~ s = µ0 nIẑ,
B
(7)
onde ẑ é um vetor unitário ao longo do eixo de simetria do solenóide, µ0 = 4π.10−7 Vs/Am, I é a
corrente elétrica através do solenóide e n é a densidade linear de espiras (quantidade de espiras por
unidade de comprimento). Nosso solenóide, representado na Fig.5, tem 80cm de comprimento e um